Навигация
ОТЧЕТ-ИТОГ 33333333333333333333
80420
знаков
0
таблиц
2
изображения
33333333333333333333 ОТЧЕТ-ИТОГ 33333333333333333333
*** Протокол множественной линейной регрессии ***
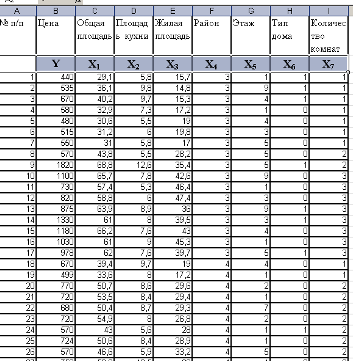
Зависимая переменная Y - y
Функция Y = +59.951+0.215*x3-0.192*x4
Оценки коэффициентов линейной регрессии
┌───┬──────────┬───────────┬───────────────┬───────────┬────────┬─────────┐
│ N │ Значение │ Дисперсия │ Средне- │ t - │ Нижняя │ Верхняя │
│ │ │ │ квадатическое │ значение │ оценка │ оценка │
│ │ │ │ отклонение │ │ │ │
├───┼──────────┼───────────┼───────────────┼───────────┼────────┼─────────┤
│ 1 │ 59.95 │ 13.80 │ 3.71 │ 16.14 │ 53.55 │ 66.35 │
│ 2 │ 0.22 │ 0.00 │ 0.05 │ 4.40 │ 0.13 │ 0.30 │
│ 3 │ -0.19 │ 0.00 │ 0.05 │ -3.71 │ -0.28 │ -0.10 │
└───┴──────────┴───────────┴───────────────┴───────────┴────────┴─────────┘
Кpитические значения t-pаспpеделения
пpи 22 степенях свободы
веpоятность t-значение
0.900 1.324
0.950 1.722
0.990 2.511
Оценки коэффициентов интерпретации линейной регрессии
╔════╤════════╤═════════╤═════════╗
║ N │Коэффиц.│Вета- │Дельта- ║
║ │эластичн│коэффиц. │коэффиц. ║
╠════╪════════╪═════════╪═════════╣
║1 │ +0.094│ +0.587│ +0.582║
║2 │ -0.241│ -0.495│ +0.418║
╚════╧════════╧═════════╧═════════╝
Таблица остатков
┌────┬──────────────┬───────────┬────────────┬───────────────┐
│ N │ Эмпирическое │ Расчетное │ Ошибка │ Ошибка │
│ │ значение │ значение │ абсолютная │ относительная │
├────┼──────────────┼───────────┼────────────┼───────────────┤
│ 1 │ 63.00 │ 56.40 │ 6.60 │ 0.10 │
│ 2 │ 44.50 │ 44.10 │ 0.40 │ 0.01 │
│ 3 │ 46.00 │ 47.16 │ -1.16 │ -0.03 │
│ 4 │ 56.50 │ 56.30 │ 0.20 │ 0.00 │
│ 5 │ 48.50 │ 45.94 │ 2.56 │ 0.05 │
│ 6 │ 47.20 │ 44.22 │ 2.98 │ 0.06 │
│ 7 │ 51.00 │ 47.97 │ 3.03 │ 0.06 │
│ 8 │ 37.00 │ 46.88 │ -9.88 │ -0.27 │
│ 9 │ 54.00 │ 54.68 │ -0.68 │ -0.01 │
│ 10 │ 42.20 │ 45.53 │ -3.33 │ -0.08 │
│ 11 │ 45.00 │ 54.55 │ -9.55 │ -0.21 │
│ 12 │ 64.50 │ 60.18 │ 4.32 │ 0.07 │
│ 13 │ 60.60 │ 59.44 │ 1.16 │ 0.02 │
│ 14 │ 52.00 │ 54.60 │ -2.60 │ -0.05 │
│ 15 │ 53.30 │ 53.21 │ 0.09 │ 0.00 │
│ 16 │ 57.80 │ 57.93 │ -0.13 │ -0.00 │
│ 17 │ 53.00 │ 51.65 │ 1.35 │ 0.03 │
│ 18 │ 61.50 │ 51.91 │ 9.59 │ 0.16 │
│ 19 │ 53.30 │ 52.71 │ 0.59 │ 0.01 │
│ 20 │ 52.00 │ 55.28 │ -3.28 │ -0.06 │
│ 21 │ 48.50 │ 50.61 │ -2.11 │ -0.04 │
│ 22 │ 52.30 │ 51.59 │ 0.71 │ 0.01 │
│ 23 │ 50.60 │ 50.86 │ -0.26 │ -0.01 │
│ 24 │ 51.00 │ 48.09 │ 2.91 │ 0.06 │
│ 25 │ 60.80 │ 64.35 │ -3.55 │ -0.06 │
└────┴──────────────┴───────────┴────────────┴───────────────┘
Характеристики остатков
Среднее значение..................... 0.000
Оценка дисперсии..................... 17.1
Оценка приведенной дисперсии........ 19.4
Средний модуль остатков.............. 2.920
Относительная ошибка аппроксимации... 0.058
Критерий Дарбина-Уотсона............. 1.864
Коэффициент детерминации............. 0.609
F - значение ( n1 = 3, n2 = 22)... 1.18e+03
Гипотеза о значимости уравнения
не отвергается с вероятностью 0.950
Использованная литература:1. Френкель А.А., Адамова Е.В. Корреляционный и регрессионный анализ в экономических приложениях: Учебное пособие / МЕСИ – М:, 1987 г.
Мхитарян В.С., Трошин Л.И., Адамова Е.В., Шевченко К.К., Бамбаева Н.Я. Теория вероятностей и математическая статистика / Московский международный институт эконометрики, информатики, финансов и права. – М., 2002 г. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М., ЮНИТИ-ДАНА, 2001 г. Колемаев В.А. и др. Теория вероятностей и математическая статистика. Учеб. пособие для экон. спец. вузов. – М., Высшая школа, 1991 г. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для втузов. Изд. 5-е, переработанное и дополненное. М., Высшая школа, 1977 г.Похожие работы
... исходить из вида обрабатываемых данных. В соответствии с современными воззрениями делим эконометрику и прикладную статистику на четыре области: - статистика случайных величин (одномерная статистика); - многомерный статистический анализ; - статистика временных рядов и случайных величин; - статистика объектов нечисловой природы. В первой области элемент выборки - число, во второй - вектор, в ...
... . При этом анализироваться могут как объекты (как точки, задаваемые в признаковом пространстве), так и признаки (как точки, задаваемые в объектном пространстве). Прикладное значение многомерного статистического анализа состоит в основном в решении следующих трех задач: · задача статистического исследования зависимостей между рассматриваемыми показателями; · задача классификации элементов ( ...
Использование корреляционно-регрессионного анализа для обработки экономических статистических данных
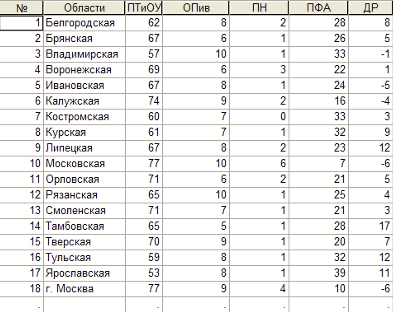
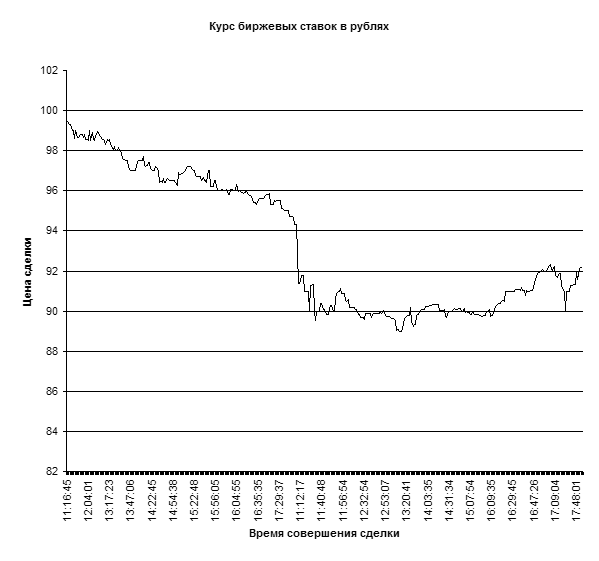
... быстро выполняемой счетной операцией. Данная работа посвящена изучению возможности обработки статистических данных биржевых ставок методами корреляционного и регрессионного анализа с использованием пакета прикладных программ Microsoft Excel. Роль корреляцонно-регрессионного анализа в обработке экономических данных Корреляционный анализ и регрессионный анализ являются смежными разделами ...
... ŷ = a0 + a1x , где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии; a0 , a1 - коэффициенты (параметры) уравнения регрессии. Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования ...
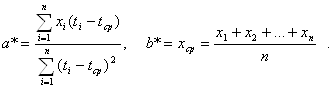
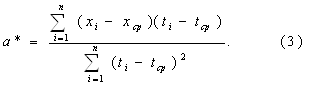
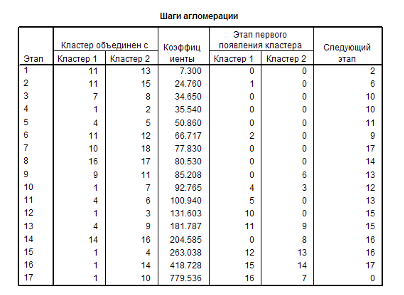
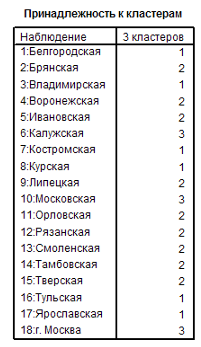
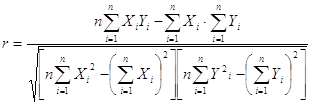
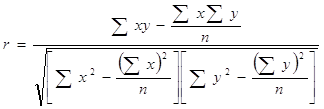
0 комментариев