Навигация
Графический анализ устойчивости сырья
1.6 Графический анализ устойчивости сырья
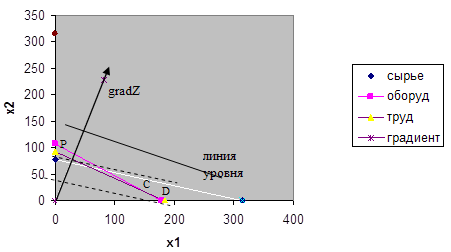
Количество используемого сырья S=х1 + 42 .
Если SÎ[0; S(D)], то точкой максимума является точка E(0; x1) пересечения оси Ох1 и прямой ограничения по сырью (1).
Если SÎ[S(D); S(C)], то точкой максимума является точка R(x1; x2) отрезка DC пересечения прямой ограничения по сырью и прямой (2)
Если SÎ[S(C); S(Р)], то точкой максимума является точка Q(x1; x2) отрезка CР пересечения прямой ограничения по сырью и прямой (3)
Если SÎ[S(Р); ¥], то точкой максимума является точка Р(0; x2) пересечения прямой (3) и оси Ох2.
Координаты точки Е находятся из системы уравнений
х1 + 4х2 = S
х2 = 0
Решаем ее:
х1 = S , х2 = 0.
Z*(S) = 165х1* + 456х2* =165S; u1 = 165; u2= 0; u3 = 0
Координаты точки R находим из системы уравнений
х1 + 4х2 = S
3х1 + 5х2 =535
Решаем ее:
х1 = (2140 - 5S)/7, х2 = (3S-535)/7.
Z*(S) = 165х1* + 456х2* = 165 ´ (2140 - 5S)/7+ 456´ (3S-535)/7= 77,6S+ 15591,4;
u1 = 77,6; u2= 0; u3 = 0.
Координаты точки Q находим из системы уравнений
х1 + 4х2 = S
2х1 + 4х2 = 368
Решаем ее:
х1 = 368-S, х2 = (2S-368)/4.
Z*(S) = 165х1* + 456х2* = 165 ´ (368-S)+ 456´ (2S-368)/4= 63S+ 18768;
u1 = 25; u2= 0; u3 = 0.
Координаты точки Р
х1 = 0, х2 =92.
Z*(S) = 165х1* + 456х2* = 41952
u1 = 0; u2= 0; u3 = 0.
S(D)= х1 + 4х2 =178,3+4´0=178,3,
S(C)= х1 + 4х2 =150+4´17=218
S(Р)= х1 + 4х2 =0+4´92=368
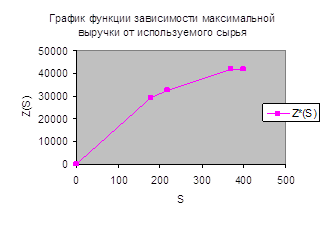
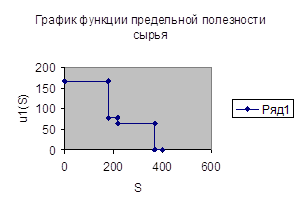
| S | 0£S<178,3 | 178,3£S<218 | 218£S<368 | S³368 |
| u1*(S) | 165 | 77,6 | 63 | 0 |
| Z*(S) | 165S | 77,6S+ 15591,4 | 63S+ 18768 | 41952 |
Интервал устойчивости [218;368)
2. Задача 2
Малое предприятие намерено организовать в следующем квартале выпуск продукции А и Б, пользующейся высоким спросом на рынке. Предприятие располагает необходимым сырьем и оборудованием и может привлечь квалифицированных рабочих на условиях почасовой оплаты, но не имеет средств на оплату труда рабочих. Для этого оно может получить в банке кредит сроком на три месяца под 40% годовых с погашением кредита и процентов по нему в конце квартала.
Информация о нормах затрат сырья, оборудования и трудовых ресурсов, объемах сырья и парка оборудования, имеющихся в распоряжении предприятия, размер выручки от реализации продукции А и Б приведены в таблице:
| Наименование ресурсов | Норма затрат на | Объем ресурса | |
| Продукт А | Продукт В | ||
| Сырье (кг) | 3 | 3 | 2070 |
| Оборудование (ст.час.) | 3 | 5 | 2250 |
| Трудоресурсы(чел.час.) | 2 | 3 | ? |
| Цена реализации (руб.) | 638 | 660 | |
Целью организации выпуска новой продукции является получение максимальной суммарной прибыли, которая определяется как разность между суммарной выручкой, полученной от реализации произведенной за квартал продукции А и Б, и затратами, связанными с обеспечением кредита (возврат суммы кредита и начисленных процентов).
Требуется:
1. Построить математическую модель оптимизации выпуска продукции с использованием кредита для выплаты зарплаты рабочими с произвольной почасовой ставкой t (руб./чел.-час) оплаты труда.
2. Определить оптимальную программу выпуска продукции, максимальную прибыль, необходимый размер кредита, сумму уплаченных процентов и потребность в трудовых ресурсах, если почасовая ставка t оплаты труда равна 10 руб./чел.-час.
3. Найти функцию спроса на трудовые ресурсы, как функцию почасовой ставки оплаты труда t, построить график этой функции. Исследовать зависимость размеров максимальной прибыли и кредита, обеспечивающего ее получение, от почасовой ставки t оплаты труда в диапазоне от 10 до 30 рублей за чел.-час. Найти функции, выражающие эти зависимости, и построить их графики.
Решение.
2.1 Построение математической модели оптимизации выпуска продукции. Для построения модели введем следующие обозначения:
х1 – объем выпуска продукции А,
х2 – объем выпуска продукции Б,
S – потребность в трудовых ресурсах,
t – почасовая ставка оплаты труда,
V – размер кредита,
Z – выручка от реализации произведенной продукции,
P – прибыль предприятия.
Выразим в математической форме основные условия и ограничения рассматриваемой задачи.
Ограничения по использованию сырья: 3x1 + 3x2 £ 2070;
Ограничения по использованию оборудования: 3x1 + 5x2 £ 2250;
Потребность в трудовых ресурсах S определяется необходимыми затратами труда для выпуска продукции в объемах х1 и х2: S = 2x1 + 3x2 .
Размер необходимого кредита определяется, исходя из потребности в трудовых ресурсах S и почасовой ставки оплаты труда t, т.е. V=tS = t(2x1 + 3x2). Выручка от реализации произведенной продукции: Z = 638x1 + 660x2
Сумма расходов по обслуживанию кредита определяется размером возвращаемого кредита и процентов по нему, т.е. равна
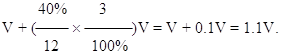
Прибыль предприятия определяется как разность между выручкой и расходами по обслуживанию кредита, т.е.
Р = Z – 1.1V.
Подставляя в эту формулу выражения для Z и V, получим
Р = (638x1 + 660x2)– 1,1 t(2x1 + 3x2) = (638 – 2,2t)х1 + (660 – 3,3 t)х2
Следовательно, математическая модель оптимизации выпуска продукции с привлечением кредитных ресурсов для оплаты труда рабочих принимает следующий вид:
Найти неизвестные значения объемов выпуска х1, х2, удовлетворяющих ограничениям
3x1 + 3x2 £ 2070
3x1 + 5x2 £ 2250 (1)
х1³0, х2³0,
и доставляющих максимальное значение целевой функции:
Р = (638 – 2,2t)х1 + (660 – 3,3 t)х2 → max.
При этом необходимый размер кредита V определяется по формуле:
V = tS = 2tx1* + 3tx2*,
где х1*, х2* - оптимальное решение задачи (1). Модель (1) представляет собой задачу параметрического линейного программирования, так как в ее условиях содержится параметр t, от значения которого зависит оптимальное решение.
2.2 Определение оптимальной программы выпуска продукции. При фиксированной ставке оплаты труда t = 10 руб./чел.-час. математическая модель (1) примет вид:
3x1 + 3x2 £ 2070
3x1 + 5x2 £ 2250
х1³0, х2³0, Р = 616 х1 + 627х2 → max.
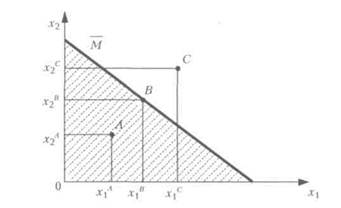
Графическое решение задачи изображено на рис. Точкой максимума является точка В с координатами х1* = 600, х2*= 90. Максимальный размер прибыли: Р* = 616´600 + 627 ´90= 426030 (руб.). Размер необходимого кредита: V* = 2tx1* + 3x2* = 2´10´600 + 3´10´90 =14700 руб. Сумма уплаченных процентов: 0,1V* = 0,1´ 14700= 1470руб. Потребность в трудовых ресурсах: S* = 2x1* +3 x2* = 2´600 + 3´90 = 1470(чел.-час.).
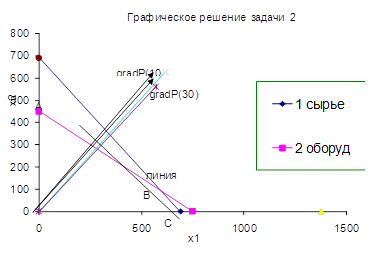
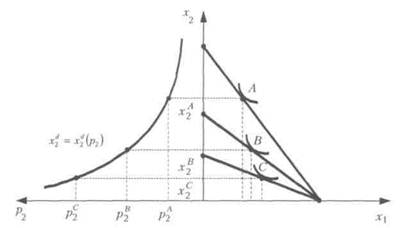
2.3 Нахождение функции спроса на трудовые ресурсы. Потребность в трудовых ресурсах S для обеспечения оптимального выпуска в объемах х1*, х2* определяются соотношением: S* = 2x1* + 3x2*.
Но оптимальный план выпуска Х* = (x1* , x2*), зависит от почасовой ставки t оплаты труда. Следовательно, величина S также зависит от t, т.е. потребность в трудовых ресурсов S есть некоторая функция от параметра t.
Найдем эту функцию. Для этого рассмотрим модель (1) и определим оптимальные планы выпуска Х* = (x1* , x2*) при различных значениях t, используя графический метод решения задачи линейного программирования.
Пусть t достаточно мало (близко к нулю). Рассмотрим уравнение линии уровня целевой функции Р = (638 – 2,2t)х1 + (660 – 3,3 t)х2= h.
При малых значениях t прямая с таким уравнением будет почти параллельна прямой с уравнением Р = 638 х1 + 660 х2 = h.
Если "закрепить" линию уровня в т.В и начать увеличивать значение параметра t, то точка пересечения линии уровня с осью Ох2 начнет перемещаться вверх по оси Ох2.
Найдем значение t, при котором линия уровня параллельна ВС. Из равенства угловых коэффициентов получаем: ![]() , t =20
, t =20
Следовательно, точка В (600;90) остается точкой максимума пока tÎ[0;20).
Найдем максимальный размер прибыли для tÎ[0;20):
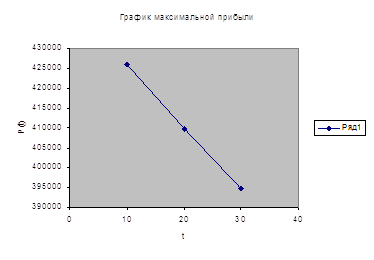
Р* = (638 – 2,2t) ´600 + (660 – 3,3 t)´90 = 442200- 1617t (руб.),
Размер необходимого кредита:
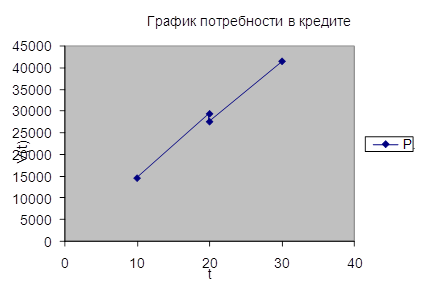
V* = 2tx1* + 3x2* = 2´t´600 +3´t´90 = 1470t руб.,
Сумма уплаченных процентов: 0,1V* = 0,1´ 1470t = 147t руб.
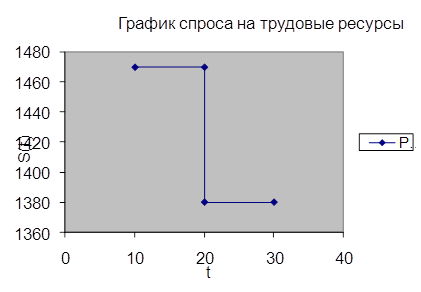
Потребность в трудовых ресурсах: S* = 2x1* + 3x2* = 2´600 +3´90 =1470 (чел.-час.).
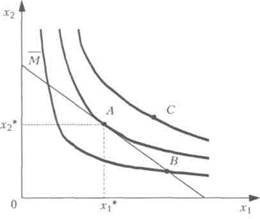
Если t=20, то оптимальное решение будет достигаться на отрезке ВС, концы которого имеют координаты В(600;90) и C(690;0).
Если "закрепить" линию уровня в т.С и начать увеличивать значение параметра t, то линия уровня будет приближаться к оси Ох1.
Найдем значение t, при котором линия уровня параллельна оси Ох1. Из равенства угловых коэффициентов получаем: ![]() ; t = 220 > 60.
; t = 220 > 60.
Если tÎ[20; 30] точкой максимума станет точка С(690;0).
Найдем максимальный размер прибыли для tÎ[20;30]:
Р* = (638 – 2,2t) ´690 + (660 – 3,3 t)´0 = 440220 – 1518t (руб.),
Размер необходимого кредита:
V* = 2tx1* + 3x2* = 2´t´690 +3´t´0=1380t руб.,
Сумма уплаченных процентов: 0,1V* = 138tруб.
Потребность в трудовых ресурсах: S* = 2x1* + 3x2* = 2´690 +3´0 = 1380(чел.-час.). Итоги решения задачи представим в таблице:
| Почасовая оплата труда t (руб.) | Оптималь-ный план выпуска Х*(t)= (x1*,x2*) | Величина спроса на трудовые ресурсы S*(t) (чел.-час.) | Размер необходимого кредита V*(t), (руб.) | Величина максимальной прибыли Р*(t) (руб.) |
| t = 10 | (600;90) | 1470 | 14700 | 426030 |
| tÎ(10;20) | (600;90) | 1470 | 1470t | 442200- 1617t |
| t = 20 | Отрезок ВС | [1380; 1470] | [27600;29400] | 409860 |
| tÎ(20;30] | (690;0) | 1380 | 1380t | 440220 – 1518t |
3. Задача 3
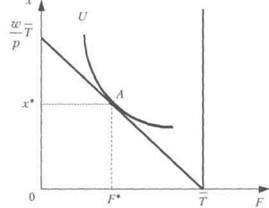
Максимизация объема выпускаемой продукции в условиях ограниченных финансовых ресурсов. Фирма при производстве продукции использует два вида ресурсов: рабочую силу (L, тыс. чел.-час.) и оборудование (K, тыс. ст.-час.). Производственная функция (ПФ) фирмы, построенная путем обработки статистических данных, имеет вид:
![]() ,
,
где Y — объем выпуска продукции (ед.).
Требуется:
Похожие работы
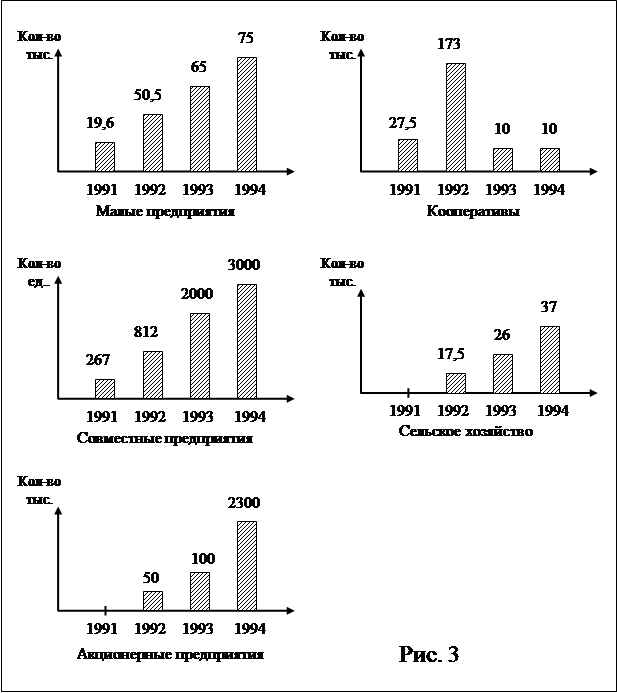
... ); · Глобализация экономики – это процесс формирования системы международного разделения труда, мировой структуры, мировой валютной системы, международной миграции труда; · Развитие общественного труда и производства. Система социально-трудовых отношений в Украине начала формироваться с 1991г. в связи с принятием законов О труде, Об оплате труда, О коллективных договорах и ...
... как можно измерить полезность определенного набора благ, которые может выбрать индивидуум. В экономической теории в этом плане есть две концепции: количественная и порядковая. Сущность количественной концепции полезности, теоретические основы которой заложены представителями австрийской экономической школы в конце XIX в. (К. Менгер, Ф. Визер, Э. Бем-Баверк и др.), состоит в том, что индивидуум в ...
... и инновационной деятельности, эффективно реализующих комплексные проекты восстановления и развития отечественных производств и территорий. Базовыми понятиями инновационной экономики являются инновация, инновационная деятельность, инновационная инфраструктура. От их правильного понимания во многом зависят тактика и стратегия формирования эффективной инновационной экономики в стране. Инновации, ...
... на принципах предпринимательства. Поэтому сегодня возврат к предпринимательству - это возврат к цивилизации, это путь выхода из тупика, в который нас завели глашатаи «строительства коммунизма». Предпринимательство, как элемент бизнеса, не может быть отделено от труда, от ведения хозяйства, от присвоения. Без труда бизнеса не бывает. Труд и предпринимательство - это процессы целенаправленной ...


0 комментариев