Навигация
Степенные средние величины
2.1 Степенные средние величины
2.1.1 Средняя арифметическая величина
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.
Иначе можно сказать, что средняя арифметическая величина - среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности.
Средняя арифметическая – наиболее распространенный на практике вид средних. Различают 2 вида арифметических средних:
· Невзвешенную (простую);
· Взвешенную.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:
![]() .
.
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:
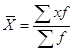 .
.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. Например, по табл.2.1.1 можно минимальный возраст рабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50-65 лет.
Таблица 2.1.1 Распределение рабочих предприятия по возрасту
| Группы рабочих по возрасту, лет | Число рабочих fj | Середина интервала xj | xj fj |
| До 20 | 48 | 18,5 | 888 |
| 20-30 | 120 | 25 | 3000 |
| 30-40 | 75 | 35 | 2625 |
| 40-50 | 62 | 45 | 2790 |
| Старше50 | 54 | 57,5 | 3105 |
| Итого | 359 | 34,56 | 12408 |
Средний возраст рабочих, рассчитанный по формуле с заменой точных значений признака в группах серединами интервалов, составил:
![]()
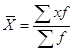 =
= ![]() ,
,
что и записано в итоговую строку по графе 3 табл.2.1.1.
Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. ![]() .
.
Это свойство определено требованиями правильного исчисления средней, согласно которым конкретные значения варьирующего признака уравниваются без изменения общего объема его и заменяются одним средним числом, которое как постоянный множитель выносится из-под знака суммы. Благодаря этому свойству средняя может быть использована для разного рода плановых и статистических расчетов как представитель или заменитель всех значений варьирующего признака. Так, если средний расход горючего на 1 гектар пахоты составляет 20 литров, а всего надо вспахать 2 млн. га, то всего потребуется 40 млн. литров горючего. Аналогично, если достаточно репрезентативное выборочное обследование показало, что среднегодовой надой молока на одну корову составляет 2500 литров, а всего в районе 15 тыс. коров, то общий надой составит 37,5 млн. литров.
2. Сумма отклонений вариантов как от простой, так и от взвешенной средней арифметической равна нулю:
![]() и
и ![]()
Рассмотренное свойство может быть использовано для проверки правильности исчисления средней. Если при исчислении средней арифметической ![]() и
и ![]() не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
3. Сумма квадратов отклонений вариантов как от простой, так и от взвешенной средней меньше суммы квадратов отклонений от любой другой произвольной величины а, т. е.
![]() .
.
Пример:
Таблица 2.1.2
| Табельный номер рабочего | 1 | 2 | 3 | 4 | 5 | 6 |
| Часовая выработка деталей (x) | 12 | 10 | 6 | 10 | 12 | 10 |
![]()
В примере, основанном на данных табл. 2.1.2, ![]() , а
, а
![]()
При а =12 ![]() составит:
составит:
Таблица 2.1.3
| xi | - a |
|
|
| 12 | -12 | 0 | 0 |
| 10 | -12 | -2 | 4 |
| 6 | -12 | -6 | 36 |
| 10 | -12 | -2 | 4 |
| 12 | -12 | 0 | 0 |
| 10 | -12 | -2 | 4 |
|
|
| Итого | 48 |
Как видим, 24<48.
Похожие работы
... расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени ...
... 21 2,0 2,8 3,8 22 2,0 2,8 3,7 23 2,0 2,8 3,7 24 2,0 2,7 3,7 25 2,0 2,7 3,7 26 2,0 2,7 3,7 27 2,0 2,7 3,6 28 2,0 2,7 3,6 29 2,0 2,7 3,6 30 2,0 2,7 3,6 ¥ 1,9 2,5 3,3 ТЕСТЫ к практическому занятию по теме «Средние величины, оценка разнообразия признака в вариационном ряду. Оценка достоверности» 1. Средние величины применяются для характеристики ...
... медианой. По такому же принципу легко найти значение признака у любой единицы ранжированного ряда. Таким образом, для расчёта средней величины вариационного ряда можно использовать целую совокупность показателей. 3. Основные показатели вариации и их значение в статистике При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчётом средней величины из отдельных ...
... , а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений. Следовательно, средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в ...

0 комментариев