Навигация
2.2.2 Мода
Мода (Мо) - это вариант признака, который при данном сочетании причин разного порядка чаще всего встречается в вариационном ряду. Например, цена, по которой чаще всего реализуется данный товар на рынке, является модой или модальной ценой. Месячная заработная плата, которая чаще всего встречается в данном коллективе, является для него модальной заработной платой.
Мода - типичная величина, в том смысле, что она встречается в совокупности или объективно может встретиться чаще других. Она имеет важное значение для решения некоторых задач, например какой высоты должны быть предназначенные для массового потребления станки, столы и т. п., какое количество детей чаще всего встречается в семье, какое время дня является «пиковым» для работы предприятий общественного питания, электростанций, городского транспорта и др., какой уровень выполнения плана наиболее часто встречается в том или ином коллективе рабочих или предприятий и т. п.
Мода соответствует определенному значению признака. На практике моду находят, как правило, по сгруппированным данным.
В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой.
В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, то есть число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу:\
![]() ,
,
XMo - нижнее значение признака X в модальном интервале;
i - величина интервала;
fMo-частота (частость) повторения признака X в модальном интервале;
fMo-1 ,fMo+1 - соответственно частоты (частости) признака для интервала, предшествующего модальному и следующего за ним.
Пример: Таблица 2.2.2
| Удойность в среднем от одной коровы за год, кг | Процент хозяйств |
| До 1000 | 7,6 |
| 1000-1649 | 9,7 |
| 1650-1999 | 16,1 |
| 2000-2499 | 37,5 |
| 2500-2999 | 20,6 |
| 3000-3999 | 8,2 |
| 4000 и выше | 0,3 |
| 100 |
По табл.2.2.2. модальный интервал составляет 2000 - 2499шт, так как ему соответствует наибольшая частота 37,5%, нижняя его граница хо = 2000, а величина интервала h = 500. Следовательно,
![]()
Это значит, что чаще всего встречаются хозяйства, у которых надой в среднем от одной коровы составляет 2280 кг.
Для решения практических задач наибольший интерес представляет обычно мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления. Выраженная в виде дискретного числа мода часто не отвечает этому требованию. Так, в нашем примере процент хозяйств, у которых годовой надой в среднем на одну корову составляет 2280 кг, хотя и больше, чем хозяйств с любым другим уровнем надоя, но сам по себе он может быть небольшим. Хозяйств же с удойностью в пределах интервала 2000 - 2499 кг - 37,5%, а 2000 - 3000 кг - 58,1, - т. е. весьма значительный процент.
3. Основные методологические требования расчета средних величин
В связи с тем, что различные виды средних приводят к разным результатам, возникает проблема правильного выбора формы средней. Если форма выбрана неправильно, то средняя будет завышена либо занижена. Так как любая средняя рассчитана на отображение лишь одного какого-либо конкретного свойства совокупности, то, следовательно, ответ может быть только однозначным. Кроме того, каждая средняя имеет свой особый смысл и область применения.
Рассматривая вопрос о выборе формы средней, которая наилучшим образам отвечает требованиям, К. Джини пишет: «Для выбора такой средней можно наметить лишь общие нормы, решающую же роль здесь играет интуиция и искусство исследователя»[1]. Как, однако, ни важны эти качества исследователя, как и общие соображения об особенностях различных средних и их назначении, решающим в выборе формы средней является социально-экономическое содержание явления, сущность которого должна найти свое количественное выражение в средней. Средняя должна, на основе обобщения количественной стороны массовых общественный явлений в неразрывной связи с их качественной стороной, дать ответ на конкретные вопросы, выдвигаемые жизнью. Поэтому для правильного решения вопроса о выборе формы средней необходимо прежде всего учесть сущность объекта, законы его развития, его специфику, определить задачу, которая должна решаться при помощи средней, и исходя из всего этого установить определяющий показатель, который должен найти отражение в средней. Таков первый этап в решении вопроса о форме средней.
Второй этап в выборе формы средней заключается в определении характера связи между определяющим свойством и осредняемым признаком. Если, например, связь прямо пропорциональна, то для расчета средней надо воспользоваться формулой средней арифметической, а при обратной пропорциональности — формулой средней гармонической. В случаях, когда связь выражается в форме геометрической прогрессии, средняя должна исчисляться по формуле средней геометрической и т. п.
Третий этап практически сводится к исчислению числовых значений средней по избранной формуле на основе фактических данных.
Из всех трех этапов наиболее сложным является первый. Недоучет некоторых обстоятельств на этом этапе или формальный подход, оторванный от качественного анализа, приводит нередко к тому, что разные авторы предлагают для решения одной и той же задачи разные виды средних.
Так как средние, включая и распределительные средние, привлекаются для получения типичных характеристик совокупности, то выбор формы средней для решения той или иной задачи зависит и от того, о какой типичности идет речь. Для характеристики однородности совокупности, устойчивости или изменчивости явлений и процессов следует привлекать среднее линейное отклонение, среднее квадратическое отклонение и коэффициент вариации. В тех случаях, когда для решения той или иной задачи важно знать размер признака, который чаще всего встречается в совокупности, надо пользоваться модой, а для того, чтобы установить границу между высшей и низшей группами величин, а также для решения некоторых оптимальных задач, — медианой. Так как различные виды средней по-разному характеризуют совокупность, то для всестороннего ее изучения надо сочетать различные виды средних величин.
Таковы научные основы выбора формы средней.
Заключение
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Средние величины делятся на два больших класса: степенные средние, структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая, средняя гармоническая, средняя кубическая.
В качестве структурных средних рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным. Взвешенная средняя считается по сгруппированным данным.
Общие формулы расчета степенных средних имеют показатель степени (m).
· средняя гармоническая, если m = - 1;
· средняя геометрическая, если m → 0;
· средняя арифметическая, если m = 1;
· средняя квадратическая, если m = 2;
· средняя кубическая, если m = 3.
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина.
Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины.
Использованная литература
1. Теория статистики: Учебно – методический комплекс / Под ред. В.В. Глинского, В.Г. Ионина, Л.И. Яковенко. – Новосибирск: НГУЭУ, 2007. – 108 с.
2. Общая теория статистики: Учебник / А.Я. Боярский, Л.Л. Викторова, А.М. Гольдберг и др.; Под ред. А.М. Гольдберга, В.С. Козлова. – М.: Финансы и статистика,1985. – 367 с.
3. Громыко Л.Г.Общая теория статистики: Практикум. – М.: ИНФРА – М,1999. – 139 с.
4. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И.И.Елисеевой. – М.: Финансы и статистика, 1996. – 368 с.: ил.
5. Пасхавер И.С. Средние величины в статистике. – М.: Статистика, 1979. – 279 с., ил.
6. Практикум по теории статистики: Учеб. пособие / Под ред. Р.А. Шмойловой. – М.; Финансы и статистика, 2001. – 416 с.: ил.
7. Статистика: учебник / Л.П. Харченко, В.Г. Ионин, В.В. Глинский и др.; под ред. канд. экон. наук, проф. В.Г. Ионина. – 3-е изд., перераб. и доп. – М.: ИНФРА-М, 2008. – 445 с. – (Высшее образование).
8. Харченко Л.П. История статистики. Развитие методологии статистической науки: Учебное пособие. – НГУЭУ, 2005. – 144 с.
Расчетная часть
Задача 1.
Один рабочий тратит на изготовление детали 2 минуты, второй 6 минут.
Определить:
1. Средние затраты времени на изготовление 1 детали (минут).
2. Количество деталей, изготовленных за первые 2 часа рабочего дня.
3. Общие трудозатраты и время, необходимое на изготовление первой партии из 100 деталей.
Решение:
1. Средние затраты времени на изготовление одной детали (минут) определяем по формуле средней арифметической простой:
![]() =
=![]()
2. Количество деталей, изготовленных за первые 2 часа рабочего дня:
а) 60 мин.* 2 часа =120 мин.;
б) Q = ![]() , где Q – количество деталей;
, где Q – количество деталей;
T – общие затраты рабочего времени;
t – уровень трудоемкости.
120 мин./ 2 мин. = 60 деталей;
120 мин. / 6 мин. = 20 деталей;
г) 60 + 20 = 80 деталей.
3. Общие трудозатраты и время, необходимое на изготовление первой партии из 100 деталей:
![]() ,
,
Где ![]() - средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими; ti – трудоемкость изготовления единицы продукции конкретным рабочим; dTi – доля рабочего в общих затратах рабочего времени.
- средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими; ti – трудоемкость изготовления единицы продукции конкретным рабочим; dTi – доля рабочего в общих затратах рабочего времени.
dT1 = dT2 = 0,5 ч.
t1 = 0,02 ч, t2 = 0,06 ч.
![]()
T=![]() *Q
*Q
Где Т – трудозатраты; ![]() - средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими; Q – общее количество выработанной продукции.
- средняя трудоемкость изготовления изделия одного и того же вида несколькими рабочими; Q – общее количество выработанной продукции.
Т = 0,03*100 = 3 ч.
Ответ:
1. Средние затраты времени на изготовление 1 детали = 4мин.
2. Количество деталей, изготовленных за первые 2 часа рабочего дня = 80.
3. Общие трудозатраты и время, необходимое на изготовление первой партии из 100 деталей = 3ч.
Задача 2.
По сельскохозяйственному предприятию имеются следующие данные о валовом сборе зерновых культур:
| Год | Валовой сбор, тонн |
| 1990 | 162 |
| 1991 | 178 |
| 1992 | 180 |
| 1993 | 183 |
| 1994 | 185 |
| 1995 | 184 |
| 1996 | 187 |
| 1997 | 190 |
| 1998 | 192 |
| 1999 | 196 |
| 2000 | 199 |
1) Построить уравнение общей тенденции валового сбора в форме линейного тренда методами:
а) первых разностей (абсолютных цепных приростов);
б) методом серий;
в) аналитического выравнивания методов наименьших квадратов.
2) Оценить ожидаемую величину валового сбора на 2002–2003 годы.
3) Отразить на графике фактический валовой сбор зерновых, его основную тенденцию и ожидаемое значение на ближайшую перспективу.
Решение:
| Год | Валовый сбор, тонн, y | t | t2 | ty |
| <Me = A, >Me =B |
| 1990 | 162 | -5 | 25 | -810 | - | А |
| 1991 | 178 | -4 | 16 | -712 | 16 | А |
| 1992 | 180 | -3 | 9 | -540 | 2 | А |
| 1993 | 183 | -2 | 4 | -366 | 3 | А |
| 1994 | 185 | -1 | 1 | -185 | 2 | В |
| 1995 | 184 | 0 | 0 | 0 | -1 | А |
| 1996 | 187 | 1 | 1 | 187 | 3 | В |
| 1997 | 190 | 2 | 4 | 380 | 3 | В |
| 1998 | 192 | 3 | 9 | 576 | 2 | В |
| 1999 | 196 | 4 | 16 | 784 | 4 | В |
| 2000 | 199 | 5 | 25 | 995 | 3 | В |
| Итого | 2036 | - | 110 | 309 |
а) Абсолютный цепной прирост:
![]()
б) Ме = ![]()
R = 4,
![]() ,
,
![]() .
.
![]() ,
,
t=2, при P = 0,954
6-2*1,58 ≤ R ≤ 6+2*1,58
2,84 ≤ R ≤ 9,16
Число серий R = 4 укладывается в пределах случайного поведения , и гипотеза о наличии обшей закономерности снижения или возрастания во времени не может быть принята(с вероятностью ошибки 0,046).
в) ![]()
![]()
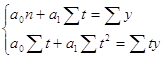 ,
,
где y – исходный уровень ряда динамики,
n – число членов ряда,
t – показатель времени.
Если ![]() ,
,
то 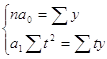 ,
, ![]()
![]() ,
, 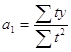 .
.
![]() ,
,
![]() .
.
Уравнение примет вид: ![]() .
.
2) Для 2002 года t =7, для 2003 года t =8, следовательно, ожидаемая величина валового сбора зерновых культур:
в 2002 году составит 185,09+2,81*7=204,76;
в 2003 году составит 185,09+2,81*8=207,57.
3)
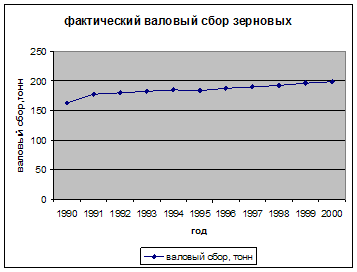
Наблюдается тенденция увеличения валового сбора зерновых.
Задача 3.
В результате 5% механической выборки в отделении банка получено следующее распределение вкладов по срокам хранения:
| Группы вкладов по сроку хранения, дней | Количество вкладов |
| До 30 | 98 |
| 30 ÷ 60 | 140 |
| 60 ÷ 90 | 175 |
| 90 ÷ 180 | 105 |
| 180 ÷ 360 | 56 |
| 360 и более | 26 |
Определить:
1) средний срок хранения вкладов по данным выборки;
2) долю вкладов со сроком хранения более 180 дней по данным выборки;
3) с вероятностью 0,954 пределы, в которых можно ожидать среднюю продолжительность хранения вклада и долю вкладов со сроком хранения более 180 дней в целом по отделению банка;
4) необходимый объем выборки при определении доли вкладов, чтобы с вероятностью 0,683 предельная ошибка не превысила 7% (0,07).
Решение:
| Группы вкладов по сроку хранения, дней | Середина интервала, x | Количество вкладов, f | xf |
|
|
|
| До 30 | 22,5 | 98 | 2205 | -85,775 | 7357,35 | 721020,3 |
| 30-60 | 45 | 140 | 6300 | -63,275 | 4003,73 | 560522,2 |
| 60-90 | 75 | 175 | 13125 | -33,275 | 1107,23 | 19376,25 |
| 90-180 | 135 | 105 | 14175 | 26,725 | 714,23 | 74994,15 |
| 180-360 | 270 | 56 | 15120 | 161,725 | 26154,98 | 1464678,88 |
| 360 и более | 540 | 26 | 14040 | 431,275 | 185998,13 | 4835951,38 |
| Итого | 600 | 64965 | - | - | 7676543,16 |
1) Средний срок хранения вкладов (дней):

2) Доля вкладов со сроком хранения более 180 дней:
![]()
Рассчитаем предельную ошибку для средней продолжительности срока хранения вкладов:
![]()
![]()
При p = 0,954 , t = 2
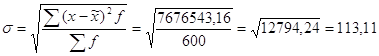
![]()
![]()
- пределы, в которых можно ожидать среднюю продолжительность хранения вклада. Предельная ошибка для доли вкладов со сроком хранения более 180 дней:
![]()
Доля вкладов = 14%, p = 0,954 , t = 2
![]() или 0,14%
или 0,14%
![]()
- пределы для доли вкладов со сроком хранения более 180 дней.
3) объем выборки при определении доли вкладов:
![]()
При p = 0,683 , t = 1
![]()
- необходимый объем выборки при определении доли вкладов
Задача 4.
Имеются данные о спросе на книжную продукцию и структуре оборота книжного издательства в отчетном году:
| Стратегическая единица | Спрос на продукцию, тыс. экз. | Доля в общем обороте издательства, % |
| 1.Классика | 20 | 0 |
| 2.Детская литература | 100 | 1,0 |
| 3.Зарубежный детектив | 60 | 49,5 |
| 4.Российский детектив | 120 | 20,5 |
| 5.Женский роман | 90 | 6,8 |
| 6.Фантастика | 50 | 0 |
| 7.Приключения | 30 | 1,0 |
| 8.Специальная литература | 110 | 14,3 |
| 9.Рекламная продукция | 60 | 4,9 |
| 10.Прочая литература | 80 | 2,0 |
Определите уровень согласованности между спросом на книжную продукцию и структурой оборота издательства с помощью коэффициентов корреляции Спирмена, Кендэла, Фехнера.
Решение:
| Стратегическая единица | Ранг | Разность рангов d= RX -RY | d2 | Баллы для расчета коэффициента Кендэлла | Знак отклонения от среднего ранга по спросу на продукцию | Знак отклонения от среднего ранга по доли в общем обороте | ||
| Спрос на продукцию RX | Доля в общем обороте RY | Q | P | |||||
| 1 – классика | 1 | 0,5 | 0,5 | 0,25 | 8 | 0 | - | - |
| 7-приключения | 2 | 1,5 | 0,5 | 0,25 | 6 | 1 | - | - |
| 6- фантастика | 3 | 0,5 | 2,5 | 6,25 | 7 | 0 | - | - |
| 3-зар.детектив | 4,5 | 8 | -3,5 | 12,25 | 0 | 6 | - | + |
| 9-рекл.продук. | 4,5 | 4 | 0,5 | 0,25 | 3 | 2 | - | - |
| 10-проч.литер. | 6 | 3 | 3 | 9 | 3 | 1 | + | - |
| 5-жен.роман | 7 | 5 | 2 | 4 | 2 | 1 | + | - |
| 2-детс.литер. | 8 | 1,5 | 6,5 | 42,25 | 2 | 0 | + | - |
| 8-спец.литер. | 9 | 6 | 3 | 9 | 1 | 0 | + | + |
| 4-рос.детектив | 10 | 7 | 3 | 9 | 0 | 0 | + | + |
| Итого: | - | - | - | 92,5 | 32 | 11 | Совпадений знаков 6; Несовпадений 4 | |
1. Корреляция Спирмена:
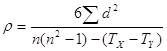 ,
,
где d – разность между рангами взаимосвязанных признаков X и Y отдельных единиц совокупности;
n – число соответствующих пар значений X и Y;
![]() ;
; ![]() ,
,
где tX – число одинаковых рангов по переменной X;
tY – число соответствующих рангов по переменной Y.
![]()
![]()
![]()

Расчетное значение статистики Стьюдента сравнивается с табличным при уровне значимости 0,05 и числе степеней свободы v = n – 2 = 10 – 2 = 8 равно 2,306.
2,306 > 1,906
2. Корреляция Кендэлла:
![]() ,
,
где
![]() ,
,
Q – число случаев, когда у последующих наблюдений ранг признака Y больше, чем у данного;
P - число случаев, когда у последующих наблюдений ранг признака Y меньше, чем у данного;
![]() ,
,
![]() ,
,
![]() ,
,
![]()
2. Корреляция Фехнера:
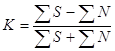 ,
,
где ![]() и
и ![]() - число совпадений и несовпадений.
- число совпадений и несовпадений.
Средний ранг равен 5,5.
![]()
Ответ: уровень согласованности между спросом на книжную продукцию и структурой оборота издательства с помощью коэффициентов корреляции Спирмена, Кендэла, Фехнера – слабая. Если ![]() , где
, где ![]() - коэффициент корреляции - связь слабая.
- коэффициент корреляции - связь слабая.
Задача 5.
Имеются данные областного комитета государственной статистики об изменении цен в текущем году по сравнению с предшествующим годом:
| Изменение цен, % | |
| 1. На платные услуги | +62,3 |
| 2. На продовольственные товары | +22,4 |
| 3. На непродовольственные товары | +20,1 |
1.Рассчитайте индекс потребительских цен, учитывая, что в текущем году сформировалась следующая структура потребления (структура потребительской корзины):
| Платные услуги | 41,0% |
| Продовольственные товары | 31,8% |
| Непродовольственные товары | 27,2% |
2.Определите величину перерасхода средств населением в текущем году за счет роста цен, если известно, что в предыдущем году было реализовано:
| Платных услуг | 5627,7 млн. руб. |
| Продовольственных товаров | 4364,9 млн. руб. |
| Непродовольственных товаров | 3728,1 млн. руб. |
Решение:
| Изменение цен,% ip*100%-100% | Реализация в текущем периоде, p1q1 | ip |
| Реализация в базисном году,
|
| |
| Платные услуги | +62,3 | 41% | 1,623 | 0,253 | 5627,7млн.руб | 9133,76 |
| Продовольственные товары | +22,4 | 31,8% | 1,234 | 0,258 | 4364,9млн.руб. | 5386,29 |
| Непродовольственные товары | +20,1 | 27,2% | 1,201 | 0,226 | 3728,1млн.руб. | 4488,63 |
| итого | 100% | 0,737 | 13720,7млн.руб. | 19008,68 |
1) ![]()
![]()
![]()
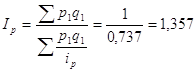 или 133,7%
или 133,7%
Цены в текущем году возросли на 33,7%.
2) 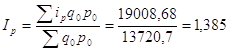 или 138,5%
или 138,5%
Перерасход средств населения за счет роста цен составил 38,5%.
[1] Джини К. Средние величины. М., Статистика, 1970. – С. 417.
Похожие работы
... расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени ...
... 21 2,0 2,8 3,8 22 2,0 2,8 3,7 23 2,0 2,8 3,7 24 2,0 2,7 3,7 25 2,0 2,7 3,7 26 2,0 2,7 3,7 27 2,0 2,7 3,6 28 2,0 2,7 3,6 29 2,0 2,7 3,6 30 2,0 2,7 3,6 ¥ 1,9 2,5 3,3 ТЕСТЫ к практическому занятию по теме «Средние величины, оценка разнообразия признака в вариационном ряду. Оценка достоверности» 1. Средние величины применяются для характеристики ...
... медианой. По такому же принципу легко найти значение признака у любой единицы ранжированного ряда. Таким образом, для расчёта средней величины вариационного ряда можно использовать целую совокупность показателей. 3. Основные показатели вариации и их значение в статистике При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчётом средней величины из отдельных ...
... , а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений. Следовательно, средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в ...

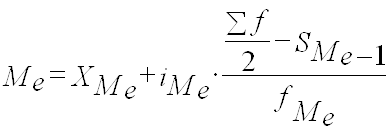
0 комментариев