Навигация
Сначала определяют, какую часть единиц генеральной совокупности надо обследовать;
1. Сначала определяют, какую часть единиц генеральной совокупности надо обследовать;
2. Последовательность отбора единиц, который достаточной мерой представляет (репрезентует) размеры средних и относительных показателей генеральной совокупности.
Преимущества выборочного наблюдения:
· Экономия времени;
· Экономия средств вследствие сокращения объёма работ статистического исследования;
· Сведение к минимуму порчи или уничтожения исследуемых объёктов (например, при контроле качества продукции (товара): определении сахаристости фруктов, клейковины в хлебе, прочности тканей на разрыв);
· Обеспечение детального изучения каждой единицы наблюдения из-за невозможности охвата всех единиц;
· Достижение высокой точности результатов наблюдения за счёт уменьшения ошибок регистрации.
Практика применения выборочного метода в экономико-статистических исследованиях использует следующие методы отбора единиц из генеральной совокупности:
1) индивидуальный отбор – в выборку отбираются отдельные единицы;
2) групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор – комбинация индивидуального и группового отборов.
Повторная выборка – из которой ранее отобранная единица возвращается в генеральную совокупность и может повторно принимать участие в выборке. Но это не всегда возможно. Например, при определении сахаристости фруктов их разрезают, то есть возврат плодов в совокупность не возможен.
Бесповторная выборка – это выборка, из которой каждая ранее отобранная единица не возвращается в генеральную совокупность и в дальнейшей выборке участия не принимает.
Бесповторный отбор даёт более точные результаты по сравнению с повторным, потому что одинаковые по объёму выборки при бесповторном исследовании охватывают больше единиц, чем повторные.
Способы формирования выборочной совокупности:
· Случайный;
· Механический;
· Типический (стратифицированный);
· Серийный (гнездовой);
Все виды отбора (кроме механического) могут быть повторными и бесповторными. Механический отбор всегда бесповторный.
Доля выборки – это отношение числа единиц выборочной совокупности ![]() к численности единиц генеральной совокупности
к численности единиц генеральной совокупности ![]() :
:
![]() .
.
Поскольку изучаемая статистическая совокупность состоит из единиц с варьирующими признаками, то состав выборочной совокупности может в той или иной мере отличаться от состава генеральной совокупности. Это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Она зависит от ряда факторов:
· степени вариации изучаемого признака;
· численности выборки;
· методов отбора единиц в выборочную совокупность;
· принятого уровня достоверности результата обследования.
Для определения средней ошибки репрезентативности собственно случайной и механической выборки используют формулы, представленные в табл. 1.
Таблица 1
Средняя ошибка репрезентативности ![]()
| Способ отбора | Определение средней | Определение выборочной доли |
| Повторный |
|
|
| Бесповторный |
|
|
где ![]() - средний квадрат отклонений в выборке;
- средний квадрат отклонений в выборке;
![]() - численность выборочной совокупности;
- численность выборочной совокупности;
![]() - численность генеральной совокупности;
- численность генеральной совокупности;
![]() - доля обследованной части выборочной совокупности;
- доля обследованной части выборочной совокупности;
![]() - необследованная часть генеральной совокупности;
- необследованная часть генеральной совокупности;
![]() - доля единиц, имеющих данный признак;
- доля единиц, имеющих данный признак;
![]() - доля единиц, не обладающих данным признаком.
- доля единиц, не обладающих данным признаком.
Для обобщающей характеристики ошибки выборки наряду со средней рассчитывают и предельную ошибку выборки. Но утверждать, что данная генеральная средняя не выйдет за пределы средней ошибки выборки можно лишь с определённой степенью вероятности. В случае выборочного наблюдения предельная ошибка репрезентативности ![]() может быть больше, равна или меньше средней ошибки репрезентативности
может быть больше, равна или меньше средней ошибки репрезентативности ![]() . Поэтому предельную ошибку репрезентативности вычисляют с определённой вероятностью
. Поэтому предельную ошибку репрезентативности вычисляют с определённой вероятностью ![]() , которой соответствует
, которой соответствует ![]() - разовое значение
- разовое значение ![]() . С введением показателя кратности ошибки
. С введением показателя кратности ошибки ![]() формула предельной ошибки репрезентативности имеет вид:
формула предельной ошибки репрезентативности имеет вид:
![]() ;
; ![]() ,
,
где ![]() - коэффициент доверия, который зависит от вероятности, с которой гарантируется значение предельной ошибки выборки.
- коэффициент доверия, который зависит от вероятности, с которой гарантируется значение предельной ошибки выборки.
Прибавляя предельную ошибку выборки к выборочной доле и отнимая её от неё, находят границы генеральной доли:
![]() и
и ![]() .
.
В таблице 2 показаны формулы для вычисления предельной ошибки собственно случайной и механичной выборки.
Таблица 2
Предельные ошибки выборки
| Способ отбора | Определение средней | Определение выборочной доли |
| Повторный |
|
|
| Бесповторный |
|
|
где ![]() - предельная ошибка выборки для средней;
- предельная ошибка выборки для средней;
![]() - предельная ошибка выборки для доли.
- предельная ошибка выборки для доли.
Во время выборочного наблюдения важно правильно определить необходимую численность выборки, которая с соответственной вероятностью обеспечивает установленную точность результатов наблюдения.
Формулы для определения необходимого объёма выборки представлены в таблице 3.
Таблица 3
Численность выборки ![]()
| Способ отбора | Определение средней | Определение выборочной доли |
| Повторный |
|
|
| Бесповторный |
|
|
Конечной целью какого-либо выборочного наблюдения является расширение его характеристик на генеральную совокупность. Выделяют два способа распространения данных выборочного наблюдения: 1) прямого пересчёта; 2) коэффициентов.
Решение типовых задач
Задача № 1.При разработке материалов городского населения методом случайного бесповторного отбора было установлено, что в городе А 15% жителей старше 60 лет. Из общей численности населения города (500 тыс. чел.) было отобрано 50 тыс. чел. С вероятностью 0,683 определите предел, в котором находится доля жителей города А в возрасте старше 60 лет.
Определите среднюю ошибку выборочной доли.
Ход решения:
Рассчитаем среднюю ошибку выборочной доли:
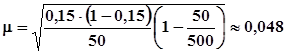 .
.
Мы использовали формулу
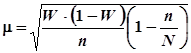 .
.
С вероятностью 0,683 предельная ошибка выборочной доли составит:
Δ = 1 х 0,048 = 0,048 (или 4,8%)
Определим верхнюю границу генеральной доли:
0,15 + 0,048 = 0,198 (или 19,8%)
Определим нижнюю границу генеральной доли:
0,15 – 0,048 = 0,102 (или 10,2%)
Вывод: С вероятностью 0,683 можно утверждать, что доля жителей в возрасте старше 60 лет в городе А колеблется от 10,2 до 19,7%.
10, 2% < р < 19,8%
Задача № 2.
Для определения средней длины детали необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество деталей надо отобрать, чтобы ошибка выборки не превышала 2 мм с вероятностью 0,954 при среднем квадратическом отклонении 8 мм.
Ход решения:
Таблица 1
Значения коэффициента доверия при выбранной вероятности
|
|
|
| 1 | 0,683 |
| 2 | 0,954 |
| 3 | 0,997 |
| 4 | 0,999 |
Рассчитаем необходимую численность выборки:
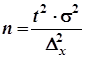
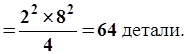
Задачи для самостоятельного выполнения
Задача №3.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности.
Задача № 4.
При обследовании 100 образцов изделий, отобранных из партии в случайном повторном порядке, оказалось 20 нестандартных. С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции в партии.
Задача № 5.
Среди выборочно обследованных 1000 семей региона по уровню среднедушевого дохода (выборка 2 %-ная, механическая) малообеспеченными оказалось 300 семей. С вероятностью 0,997 определите долю малообеспеченных семей в регионе.
Тесты для закрепления материалаТест 1
При механической выборке установлено, что в 50 партиях сыра среднее содержание влаги составило 74 %, при среднем квадратическом отклонении 1,5 %. Какие из нижеприведённых показателей нужно вычислить, чтобы установить границы влаги в сыре в генеральной совокупности:
а) дисперсию;
б) размах вариации;
в) граничную ошибку выборки;
г) коэффициент вариации.
Тест 2
Средняя ошибка выборки вычисляется с целью:
а) изучения вариации признака;
б) определения среднего значения признака, который исследуется;
в) определения коэффициента роста;
г) установление возможных границ отклонений средней генеральной от средней выборочной.
Тест 3
Чтобы уменьшить среднюю ошибку выборки в два раза, объём случайной повторной выборки нужно:
а) увеличить в два раза;
б) увеличить в четыре раза;
в) уменьшить в два раза;
г) уменьшить в четыре раза.
Литература1. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001. - 320 с.
2. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
3. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник /Под ред. О.Э. Башиной, А.А. Спирина. – 5-е изд, доп. и перераб. – М.: Финансы и статистика, 1999. – 440 с.
4. Захожай В.Б., Попов І.І., Коваленко О.В. Практикум з основ статистики: Навч. посіб. – К.: МАУП, 2001. - 176 с.
Тема 7. Статистическая проверка гипотез
План лекционных занятий13. Статистическая проверка гипотез.
13.1. Общие понятия о гипотезе.
13.2. Этапы работы по статистической проверке гипотез.
14. Дисперсионный анализ.
14.1. Критерии согласия.
14.2. Элементы дисперсионного анализа.
Методические указания
Гипотеза – это научное предположение об особенностях явлений, которые их определяют, требующее проверки и доказательства.
Статистическая гипотеза – это определенное предположение, касающееся параметров или формы распределения генеральной совокупности, которое можно проверить, опираясь на результаты выборочного наблюдения. Суть проверки гипотез заключается в том, чтобы проверить, согласуются или нет результаты выборки с гипотезой, случайными или неслучайными являются расхождения между гипотезой и данными выборки.
При проверке гипотез имеется возможность совершить ошибки двоякого рода:
а) ошибка первого рода – проверяемая гипотеза (её обычно называют нулевой гипотезой) является в действительности верной, но результаты проверки приводят к отказу от неё;
б) ошибка второго рода – проверяемая гипотеза в действительности является ошибочной, но результаты проверки приводят к её принятию.
Чаще всего гипотеза, которую необходимо проверить, формулируется как отсутствие расхождений между неизвестным параметром генеральной совокупности ![]() и заданной величиной
и заданной величиной ![]() (нулевая гипотеза), обозначается
(нулевая гипотеза), обозначается ![]() . Содержание гипотезы записывается после двоеточия, например
. Содержание гипотезы записывается после двоеточия, например ![]() .
.
Статистическим критерием называется правило, согласно которому нулевая гипотеза принимается или отклоняется. Для каждого вида проверяемых гипотез разработаны специальные критерии, среди которых чаще всего используют ![]() - критерий нормального распределения и распределения Стьюдента,
- критерий нормального распределения и распределения Стьюдента, ![]() -критерий Фишера,
-критерий Фишера, ![]() распределения Пирсона («хи-квадрат») и другие.
распределения Пирсона («хи-квадрат») и другие.
Для построения статистического критерия, позволяющего проверить некоторую гипотезу, необходимо следующее:
1) Сформулировать проверяемую гипотезу ![]() . Наряду с проверяемой гипотезой формулируется также конкурирующая гипотеза (альтернативная);
. Наряду с проверяемой гипотезой формулируется также конкурирующая гипотеза (альтернативная);
2) выбрать уровень значимости ![]() , контролирующий допустимую вероятность ошибки первого рода;
, контролирующий допустимую вероятность ошибки первого рода;
3) определить область допустимых значений и так называемую критическую область;
4) принять то или иное решение на основе сравнения фактического и критического значений критерия.
Уровень значимости (![]() ) – это такое малое значение вероятности попадания критерия в критическую область при условии справедливости гипотезы, что появление этого события может расцениваться как следствие существенного расхождения выдвинутой гипотезы и результатов выборки. Обычно уровень значимости принимают равным 0,05 или 0,01.
) – это такое малое значение вероятности попадания критерия в критическую область при условии справедливости гипотезы, что появление этого события может расцениваться как следствие существенного расхождения выдвинутой гипотезы и результатов выборки. Обычно уровень значимости принимают равным 0,05 или 0,01.
Статистические критерии, используемые для проверки гипотез, бывают двух видов:
1) Параметрическими называю критерии, которые обосновываются на допущении: распределение случайной величины в совокупности подчиняется какому-либо известному закону (например, нормальному, биноминальному, Пуассона). К таким критериям относятся критерии ![]() .
.
2) Непараметрическими (порядковыми) называют критерии, использование которых не связано со знанием закона распределения случайной величины. Их можно использовать тогда, когда распределение значительно отличается от нормального. К таким критериям относятся критерий знаков Вилкоксона, Уайта, Манна-Уитни.
Параметрические критерии значительно эффективнее непараметрических.
Мощность критерия – это вероятность отклонения испытуемой нулевой гипотезы, когда правильною является альтернативная гипотеза. То есть мощностью критерия является вероятность того, что не будет допущена ошибка. Конечно, желательно иметь более мощный критерий, так как это обеспечит минимальную вероятность допущения ошибки второго рода.
Этапы работы по проверке статистической гипотезы:
1) оценка входной информации и описание статистической модели выборочной совокупности;
2) формирование нулевой и альтернативной гипотезы;
3) установление уровня значимости, с помощью которого контролируют ошибку первого рода;
4) выбор мощного критерия для проверки нулевой гипотезы (это даёт возможность контролировать появление ошибки второго рода);
5) вычисление по определённому алгоритму фактического значения критерия;
6) определение критической области и области согласия с нулевой гипотезой, то есть установление табличного значения критерия;
7) сравнение фактического и табличного значений критерия и формулирование выводов по результатам проверки нулевой гипотезы.
Критерием согласия называют критерий проверки гипотезы на ожидаемый закон неизвестного распределения в генеральной совокупности. Есть ряд критериев согласия: Пирсона, Колмогорова, Смирнова, Ястремского. Эти критерии дают возможность установить: согласуются или нет опытные распределения с теоретическими, а также насколько существенны расхождения между распределениями.
Одним из наиболее употребляемых критериев согласия является критерий К. Пирсона ![]() («Хи-квадрат»):
(«Хи-квадрат»):
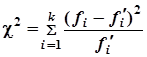 ,
,
где ![]() - соответственно частоты эмпирического и теоретического распределения в
- соответственно частоты эмпирического и теоретического распределения в ![]() - том интервале.
- том интервале.
Чем больше разность между наблюдаемыми и теоретическими частотами, тем больше величина критерия Пирсона. Чтобы отличить существенные значения ![]() от значений, которые могут возникнуть в результате случайностей выборки, рассчитанное значение критерия сравнивается с табличным значением
от значений, которые могут возникнуть в результате случайностей выборки, рассчитанное значение критерия сравнивается с табличным значением ![]() при соответствующем числе степеней свободы и заданном уровне значимости.
при соответствующем числе степеней свободы и заданном уровне значимости.
Определив значение критерия Пирсона по данным конкретной выборки, можно встретиться с такими вариантами:
1) ![]() , то есть
, то есть ![]() попадает в критическую область. Это означает, что расхождение между эмпирическими и теоретическими частотами существенно и его нельзя объяснить случайными колебаниями выборочных данных. В таком случае гипотеза о близости эмпирического распределения к нормальному отвергается.
попадает в критическую область. Это означает, что расхождение между эмпирическими и теоретическими частотами существенно и его нельзя объяснить случайными колебаниями выборочных данных. В таком случае гипотеза о близости эмпирического распределения к нормальному отвергается.
2) ![]() , то есть рассчитанный критерий не превышает максимально возможную величину расхождений эмпирических и теоретических частот, которая может возникнуть в силу случайных колебаний выборочных данных. В этом случае гипотеза о близости эмпирического распределения к нормальному не отвергается.
, то есть рассчитанный критерий не превышает максимально возможную величину расхождений эмпирических и теоретических частот, которая может возникнуть в силу случайных колебаний выборочных данных. В этом случае гипотеза о близости эмпирического распределения к нормальному не отвергается.
Табличное значение критерия Пирсона определяется при фиксированном уровне значимости и соответствующем числе степеней свободы.
Число степеней свободы = ![]() , где
, где ![]() - число условий, которые предполагаются выполненными при вычислении теоретических частот,
- число условий, которые предполагаются выполненными при вычислении теоретических частот, ![]() - число групп. Понятие числа степеней свободы связано с тем, что в статистических совокупностях приходится учитывать линейные связи, ограничивающие свободу изменения случайных величин. Например, при исчислении дисперсии в совокупности мы располагаем
- число групп. Понятие числа степеней свободы связано с тем, что в статистических совокупностях приходится учитывать линейные связи, ограничивающие свободу изменения случайных величин. Например, при исчислении дисперсии в совокупности мы располагаем ![]() степенями свободы, так как любое значение признака мы можем определить, зная
степенями свободы, так как любое значение признака мы можем определить, зная ![]() значений и среднюю арифметическую.
значений и среднюю арифметическую.
Дисперсионный анализ – это метод статистической оценки надёжности выявления зависимости результативного признака от одного или нескольких факторов. Суть этого метода заключается в статистическом изучении надёжности влияния одного или нескольких факторов, а также их взаимодействия на результативный признак.
С помощью дисперсионного анализа решаются три задачи:
1. дать общую оценку существенности отличий между групповыми средними.
2. Оценить надёжность взаимодействия факторов.
3. Оценить существенность отличий между парами средних.
Решение задач дисперсионного анализа базируется на законе сложения вариации, соответственно которому общую вариацию (колебание) результативного признака разделяют на две: вариацию, обусловленную действием исследуемого фактора (факторов), и вариацию, обусловленную действием случайных причин, то есть: ![]() .
.
Дисперсии двух выборок сравнивают, используя критерий Фишера - ![]() - критерий. Для этого вычисляют отношение большей выборочной дисперсии к меньшей:
- критерий. Для этого вычисляют отношение большей выборочной дисперсии к меньшей:
![]() .
.
Если ![]() - критерий равен 1, то это указывает на равенство дисперсий, и вопрос о существенности их расхождений снимается. Если же величина дисперсионного отношения больше 1, то возникает необходимость оценить, случайно ли расхождение между дисперсиям. При этом очевидно: чем больше величина дисперсионного отношения, тем значительнее расхождение между ними.
- критерий равен 1, то это указывает на равенство дисперсий, и вопрос о существенности их расхождений снимается. Если же величина дисперсионного отношения больше 1, то возникает необходимость оценить, случайно ли расхождение между дисперсиям. При этом очевидно: чем больше величина дисперсионного отношения, тем значительнее расхождение между ними.
Решение типовых задач
Задача № 1.В пригородном хозяйстве испытали рацион с добавкой витаминов при мясном откорме животных. Были организованы опытная и контрольная группа по 5 голов в каждой. На протяжении месяца опытная группа животных получала дополнительно комплекс витаминов. В конце месяца для каждого животного был определён прирост живой массы (табл.1). Сравнение средних суточных приростов в двух группах животных показывает, что более высокий суточный прирост дали животные исследуемой группы. Так как выборка невелика (![]() ), не исключена возможность, что расхождение в суточных приростах обусловлено действием случайных причин. Необходимо статистически оценить разницу между средними двух групп животных. По результатам проверки сделать вывод о том, что разница между средними находится в границах случайных колебаний или эта разница настолько значима, что не согласуется с нулевой гипотезой о случайном характере разницы между средними. Если будет доказано второе положение и отклонено первое, можно утверждать, что условия роста массы животных опытной группы существенно отличаются от условий контрольной группы, то есть комплекс витаминов стимулирует суточный прирост.
), не исключена возможность, что расхождение в суточных приростах обусловлено действием случайных причин. Необходимо статистически оценить разницу между средними двух групп животных. По результатам проверки сделать вывод о том, что разница между средними находится в границах случайных колебаний или эта разница настолько значима, что не согласуется с нулевой гипотезой о случайном характере разницы между средними. Если будет доказано второе положение и отклонено первое, можно утверждать, что условия роста массы животных опытной группы существенно отличаются от условий контрольной группы, то есть комплекс витаминов стимулирует суточный прирост.
Таблица 1
| № животного | Основной рацион + витамины (опыт) | Основной рацион (контроль) | Квадраты суточных приростов в группе | |
| опытной | контрольной | |||
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 632 | 520 | 399424 | 270400 |
| 2 | 691 | 586 | 477481 | 343396 |
| 3 | 570 | 490 | 324900 | 240100 |
| 4 | 694 | 609 | 781636 | 370881 |
| 5 | 683 | 590 | 466489 | 348100 |
| Всего | 3270 | 2795 | 2449930 | 1572877 |
Ход решения:
Условие задачи предусматривает, что обе выборки взяты из нормально распределённой генеральной совокупности. Формирование групп является случайным (независимым), поэтому оценивать следует разницу между средними.
Определим средние суточные приросты в опытной и контрольной группах:
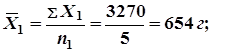
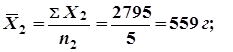
Фактическая разница между средними:
![]() .
.
Существенность этой разницы нужно оценить. Для этого проверяют гипотезу о равности двух средних.
Рассмотрим подробно все этапы проверки гипотезы.
1. Сформулируем нулевую (![]() ) и альтернативную (
) и альтернативную (![]() ) гипотезы:
) гипотезы:
![]() . (Знак «двоеточие» означает «равно»)
. (Знак «двоеточие» означает «равно»)
2. Примем уровень значимости ![]() ; он гарантирует принятие гипотезы или отказ от неё с вероятностью ошибки только в 5 случаях из 100.
; он гарантирует принятие гипотезы или отказ от неё с вероятностью ошибки только в 5 случаях из 100.
3. Самым мощным критерием для проверки такой гипотезы ![]() является
является ![]() -критерий Стьюдента (для малых выборок).
-критерий Стьюдента (для малых выборок).
4. Сформулируем правило принятия решения по результатам проверки ![]() : гипотеза
: гипотеза ![]() отклоняется, если фактическое значение
отклоняется, если фактическое значение ![]() -критерия будет больше его табличного значения, то есть, если
-критерия будет больше его табличного значения, то есть, если ![]() . В противном случае
. В противном случае ![]() должна быть принята.
должна быть принята.
5. Чтобы проверить ![]() , необходимо определить фактическое значение критерия Стьюдента и сравнить его с табличным.
, необходимо определить фактическое значение критерия Стьюдента и сравнить его с табличным.
Фактическое значение ![]() -критерия Стьюдента определим по формуле:
-критерия Стьюдента определим по формуле:
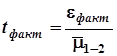 ,
,
где ![]() - обобщающая средняя ошибка разницы средних.
- обобщающая средняя ошибка разницы средних.
Для определения фактического значения ![]() -критерия Стьюдента осуществим такие расчёты.
-критерия Стьюдента осуществим такие расчёты.
6. Определим для каждой выборки скорректированные на потерю числа степеней свободы вариации дисперсии, возводя сначала значения ![]() и
и ![]() в квадрат.
в квадрат.
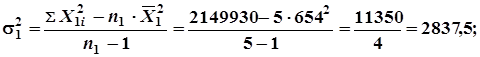
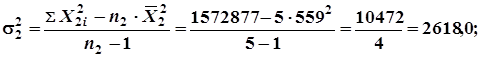
7.Определим квадраты средних шибок для каждой выборки и обобщающую среднюю ошибку разницы средних:

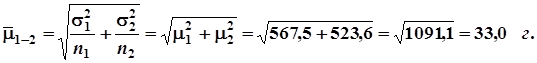
8.Вычислим фактическое значение критерия Стьюдента:
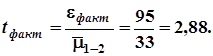
9.Установим табличное значение критерия Стьюдента, исходя из уровня значимости ![]() и общего числа степеней свободы для двух выборок:
и общего числа степеней свободы для двух выборок:
![]()
В таблице ![]() при
при ![]() и
и ![]() равно
равно ![]() .
.
10. Сопоставим фактическое и табличное значение критерия Стьюдента:
![]()
Вывод: Так как ![]() (выборочное значение критерия пребывает в критической области), нулевую гипотезу о равенстве средних в генеральной совокупности нужно отклонить и принять альтернативную гипотезу о том, что средние в генеральных совокупностях не являются равными. То есть данные опыта не согласуются с гипотезой о том, что разница между средними приростами случайна. Фактическое значение критерия Стьюдента превышает его возможную теоретическую величину, которая измеряет случайное колебание, что даёт возможность сделать вывод о существенности (достоверности) разницы между средними. Добавка комплекса витаминов в рацион стимулирует повышение среднесуточных приростов.
(выборочное значение критерия пребывает в критической области), нулевую гипотезу о равенстве средних в генеральной совокупности нужно отклонить и принять альтернативную гипотезу о том, что средние в генеральных совокупностях не являются равными. То есть данные опыта не согласуются с гипотезой о том, что разница между средними приростами случайна. Фактическое значение критерия Стьюдента превышает его возможную теоретическую величину, которая измеряет случайное колебание, что даёт возможность сделать вывод о существенности (достоверности) разницы между средними. Добавка комплекса витаминов в рацион стимулирует повышение среднесуточных приростов.
Задачи для самостоятельного выполнения
Задача №2.
В полевом опыте проверяли влияние разных компонентов минеральных удобрений на урожайность хмеля.
Таблица 1 Урожайность хмеля, ц/га
| Повторяемость | Вариант опыта | Разница | Квадрат разницы | |
| I (опыт)
| II (контроль)
| |||
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 13,6 | 10,5 | 3,1 | 9,61 |
| 2 | 16,2 | 12,4 | 3,8 | 14,44 |
| 3 | 17,9 | 15,3 | 2,6 | 6,76 |
| 4 | 13,5 | 11,7 | 1,8 | 3,24 |
| 5 | 14,8 | 13,1 | 1,7 | 2,89 |
| Всего | 76,0 | 63,0 | 13,0 | 36,94 |
| Средние | 15,2 | 12,6 | 2,6 | - |
На контрольных участках вносили фосфор и калий (![]() ), а на опытных дополнительно азот (
), а на опытных дополнительно азот (![]() ). Опыт проведён при пятикратной повторности. При распределении повторений опыта учли отличия участков по плодородию грунта, микрорельефу и другим условиям. Поэтому выборки можно рассматривать как независимые.
). Опыт проведён при пятикратной повторности. При распределении повторений опыта учли отличия участков по плодородию грунта, микрорельефу и другим условиям. Поэтому выборки можно рассматривать как независимые.
Необходимо проверить статистическую гипотезу относительно средней разницы между парами взаимосвязанных наблюдений в генеральной совокупности.
Задача № 3.
Расчёт характеристик вариационного ряда распределения 100 предприятий по размеру прибыли показал, что эмпирическое распределение достаточно близко к симметричному и характеризуется такими параметрами:
1) средняя прибыльность 27,5 тыс. грн;
2) выборочное среднее квадратичное отклонение прибыльности ![]() =6,6 тыс. грн.
=6,6 тыс. грн.
3) величина интервала ![]() =4,0 тыс. грн.
=4,0 тыс. грн.
4) численность выборочной совокупности ![]() =100.
=100.
Необходимо проверить гипотезу о соответствии эмпирического распределения предприятий нормальному.
Таблица 1
| Среднее значение интервала, тыс. грн | Фактическое количество предприятий |
| 16 | 9 |
| 20 | 45 |
| 24 | 16 |
| 28 | 24 |
| 32 | 18 |
| 36 | 12 |
| 40 | 6 |
| Всего | 100 |
Тест 1
В статистике критерий Стьюдента обозначается:
а) ![]() критерий;
критерий;
б) ![]() ;
;
в) ![]() критерий.
критерий.
Тест 2
Мощность критерия – это:
а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является альтернативная гипотеза;
б) те значения критерия, при которых нулевую гипотезу отклоняют;
в) такое малое значение вероятности попадания критерия в критическую область при условии справедливости гипотезы, что появление этого события может расцениваться как следствие существенного расхождения выдвинутой гипотезы и результатов выборки.
Тест 3
Выберите ряд критериев согласия:
а) Пирсона;
б) Колмогорова;
в) Фишера;
г) Стьюдента;
д) Смирнова;
е) Ястремского;
ж) Романовского.
Литература:
1. Ефимова М.Р. , Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.:ИНФА-М, 2002. – 416 с.
2. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001. - 320 с.
3. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
4. Мармоза А.Т. Практикум з основ статистики. К.: Ельга, Ніка-Центр, 2003. – 344 с.
5. Сборник задач по общей теории статистики. Учебное пособие. Изд. 2-е. /Под ред. Серга Л.К. – М.: Информационно-издательский дом «Филин», Рилант, 2001. – 360 с.
Тема 8. Статистические методы анализа корреляционных связей
План лекционных занятий
15. Методы анализа взаимосвязей.
15.1. Виды взаимосвязей.
15.2. Регрессионный анализ.
16. Проверка существенности корреляционной связи.
16.1. Оценка плотности.
16.2. Ранговая корреляция.
Методические указания
Все явления окружающего мира, социально-экономические в частности, взаимосвязаны и взаимообусловлены. В сложном переплетении всеобъемлющей взаимосвязи какое-либо явление является следствием действия определённого множества причин и одновременно – причиною других явлений.
Определяющая цель измерения взаимосвязей – выявить и дать количественную характеристику причинных связей. Суть причинной связи состоит в том, что в определённых условиях одно явление вызывает другое. Причина сама по себе не определяет следствие, последнее зависит также от условий, в которых действует причина. Изучая закономерности связи, причины и условия объединяют в одно понятие «фактор». Соответственно, признаки, характеризующие факторы, называют факторными, а те, которые характеризуют последствия, - результативными.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производимой продукции.
Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтённые случайные величины. По направлению связи бывают прямыми, когда зависимая переменная растёт с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
С точки зрения взаимодействующих факторов связь бывает парной – если характеризуется связь двух признаков, и множественной – если изучаются более, чем две переменные.
По виду бывают непосредственные – факторы взаимодействуют между собой непосредственно; косвенные – характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками; ложная – это связь, установленная формально и, как правило, подтверждённая только количественными оценками, она не имеет под собой качественной основы или вообще бессмысленна.
По силе различают слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.
Количественная взаимосвязь факторов называется регрессией. А важной характеристикой корреляционной связи является линия регрессии – эмпирическая в модели аналитической группировки и теоретическая в модели регрессионного анализа. Недостаток эмпирических линий состоит в небольшой точности и практически невозможной алгоритмизации полученных зависимостей.
Эмпирическая линия регрессии представлена групповыми средними результативного признака ![]() , каждая из которых принадлежит соответствующему интервалу значений группировочного фактора
, каждая из которых принадлежит соответствующему интервалу значений группировочного фактора ![]() . Теоретическая линия регрессии описывается определённой функцией
. Теоретическая линия регрессии описывается определённой функцией ![]() , которую называют уравнением регрессии, а
, которую называют уравнением регрессии, а ![]() - теоретическим уровнем результативного признака.
- теоретическим уровнем результативного признака.
Разные явления по разному реагируют на изменение факторов. Для того, чтобы отобразить характерные особенности связи конкретных явлений, статистика использует разные по функциональному виду регрессионные уравнения:
· если при изменении фактора ![]() результат
результат ![]() изменяется более-менее равномерно, такая связь описывается линейной функцией
изменяется более-менее равномерно, такая связь описывается линейной функцией ![]() ;
;
· если неравномерное соотношение вариаций взаимосвязанных признаков (например, когда прирост значений ![]() при смене
при смене ![]() ускорен или замедлен, или направление связи изменяется), используют нелинейные регрессии:
ускорен или замедлен, или направление связи изменяется), используют нелинейные регрессии:
1. Степенную ![]() ;
;
2. Гиперболическую ![]() ;
;
3. Параболическую ![]() .
.
Наряду с определением характера связи и эффекта влияния факторов ![]() на результат
на результат ![]() важное значение имеет оценка плотности связи – то есть оценка согласованности вариации взаимосвязанных признаков. Если влияние факторного признака
важное значение имеет оценка плотности связи – то есть оценка согласованности вариации взаимосвязанных признаков. Если влияние факторного признака ![]() на результативный
на результативный ![]() существенный, это проявится в закономерной смене значений
существенный, это проявится в закономерной смене значений ![]() при смене значений
при смене значений ![]() , то есть фактор
, то есть фактор ![]() своим влиянием формирует вариацию
своим влиянием формирует вариацию ![]() . При отсутствии связи вариация
. При отсутствии связи вариация ![]() не зависит от вариации
не зависит от вариации ![]() .
.
Для оценки плотности связи статистика использует группу коэффициентов с такими общими особенностями:
· при отсутствии какой-либо связи значение коэффициента приближается к нулю; при функциональной связи – к единице;
· при наличии корреляционной связи коэффициент выражается дробью, которая по абсолютной величине тем больше, чем плотнее связь.
Среди мер плотности связи самым распространённым является:
1) коэффициент корреляции Пирсона - ![]() . Поскольку сфера его использования ограничивается линейной зависимостью, то и в названии его фигурирует слово «линейный».
. Поскольку сфера его использования ограничивается линейной зависимостью, то и в названии его фигурирует слово «линейный».
Коэффициент корреляции определяется по формуле:
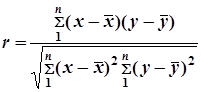 .
.
2) Коэффициент детерминации – квадрат коэффициента корреляции (![]() ), показывающий, какая часть общей вариации результативного признака определяется исследуемым фактором.
), показывающий, какая часть общей вариации результативного признака определяется исследуемым фактором.
3) Мерою плотности связи является также корреляционное отношение:
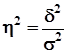 ,
,
где ![]() - межгрупповая дисперсия, которая измеряет вариацию признака
- межгрупповая дисперсия, которая измеряет вариацию признака ![]() под влиянием фактора
под влиянием фактора ![]() ,
,
![]() - общая дисперсия.
- общая дисперсия.
Корреляционное отношение показывает, сколько процентов вариации признака объясняется вариацией фактора и используется для оценки плотности связи по данным аналитической группировки (например, для оценки плотности связи между глубиной разработки угольных пластов и фондоёмкости добычи угля).
Взаимосвязь между признаками, которые можно ранжировать, прежде всего, на основе бальных оценок, измеряется методами ранговой корреляции. Упорядочение единиц совокупности по значению признака называется ранжированием. Рангами называются числа натурального ряда, которые согласно значениям признака присваиваются элементам совокупности и в определённой степени упорядочивают её. Ранжирование проводится по каждому признаку отдельно: первый ранг присваивается наименьшему значению признака, последний – наибольшему или наоборот. Количество рангов равно объёму совокупности. Учитывая то, что ранговая корреляция не требует соблюдения каких-либо математических предпосылок распределения признаков, ранговые оценки плотности связи целесообразно использовать для совокупностей небольшого объёма.
Решение типовых задач
Задача № 1.С помощью методов периодизации выделены периоды однотипной динамики безработицы и преступности.
1. По одному из таких периодов с помощью линейного коэффициента корреляции определите наличие связи между числом преступлений и численностью лиц, не занятых в экономике. Дайте оценку.
2. Постройте уравнение регрессии.
3. Нанесите на график эмпирическую и теоретическую линии регрессии.
Таблица 1
| Год | Лица в трудоспособном возрасте, не занятые в экономике, тыс. чел. | Число зарегистрированных преступлений |
| 1999 | 117,1 | 54 929 |
| 2000 | 134,7 | 77 915 |
| 2001 | 191,9 | 86 615 |
| 2002 | 215,0 | 72 404 |
Ход решения:
Так как с увеличением числа лиц в трудоспособном возрасте (![]() ), не занятых в экономике, равномерно увеличивается число зарегистрированных преступлений (
), не занятых в экономике, равномерно увеличивается число зарегистрированных преступлений (![]() ), то оценку зависимости проводим с помощью линейного уравнения регрессии, а оценку тесноты связи – линейного коэффициента корреляции.
), то оценку зависимости проводим с помощью линейного уравнения регрессии, а оценку тесноты связи – линейного коэффициента корреляции.
1. Линейный коэффициент корреляции рассчитывается по формуле:
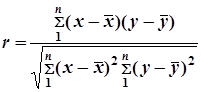 =
=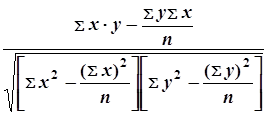 .
.
2. Уравнение прямой, с помощью которой оценивается форма зависимости изучаемых показателей, имеет вид:
![]() ,
,
где ![]() - теоретическое число зарегистрированных преступлений;
- теоретическое число зарегистрированных преступлений;
![]() - численность лиц в трудоспособном возрасте, не занятых в экономике;
- численность лиц в трудоспособном возрасте, не занятых в экономике;
![]() - параметры уравнения прямой, определяемые системой нормальных уравнений:
- параметры уравнения прямой, определяемые системой нормальных уравнений:
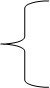
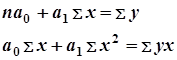 ;
;
Откуда
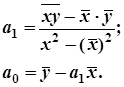 .
.
Для определения параметров уравнения регрессии и линейного коэффициента корреляции строим таблицу и находим параметры уравнения:
Таблица 2
| Годы |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1999 | 117,1 | 54 929 | 6432185,9 | 13712,41 | 65183 | 3017195041 |
| 2000 | 134,7 | 77 915 | 10495150,5 | 18144,09 | 68062 | 6070747225 |
| 2001 | 191,9 | 86 615 | 16621418,5 | 36825,61 | 77420 | 7502158225 |
| 2002 | 215,0 | 72 404 | 15566860 | 46225,00 | 81199 | 522339216 |
| Итого | 658,7 | 291 863 | 49115614,9 | 114907,11 | 291863 | 21832439707 |
Линейный коэффициент корреляции:
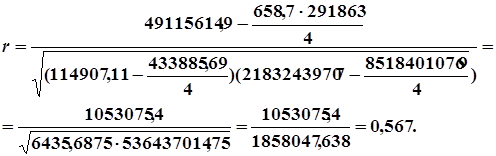
Полученное значение коэффициента корреляции свидетельствует о заметной (умеренной) связи между численностью лиц в трудоспособном возрасте, не занятых в экономике, и числом зарегистрированных преступлений.
Найдём по формулам параметры уравнения:
![]()
![]()
Уравнение корреляционной связи примет вид:
![]()
Подставив в это уравнение значения ![]() , определяют теоретические значения
, определяют теоретические значения ![]() . Так,
. Так,
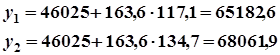 .
.
и т.д.
Теоретические значения приведены в табл. 2.
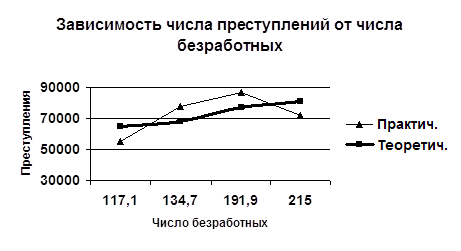
Задачи для самостоятельного выполнения
Задача №2.
По 10 совхозам есть данные об урожайности зерновых культур и качестве грунта. Необходимо провести корреляционно-регрессионный анализ связи между двумя признаками – урожайностью и качеством грунта. Для характеристики этой связи необходимо определить: 1) форму связи и математическое уравнение связи, для чего построить график корреляционной зависимости между урожайностью (![]() - результативный признак) и качеством грунта (
- результативный признак) и качеством грунта (![]() - факторный признак); 2) параметры уравнения регрессии; 3) тесноту связи (коэффициенты корреляции и детерминации).
- факторный признак); 2) параметры уравнения регрессии; 3) тесноту связи (коэффициенты корреляции и детерминации).
Таблица 1
| № | Урожайность, ц/га | Качество грунта, баллов | Расчётные величины | |||
|
|
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 28,0 | 79 | 2212,0 | 784,00 | 6241 | 27,84 |
| 2 | 21,0 | 70 | 1470,0 | 441,00 | 4900 | 19,48 |
| 3 | 27,6 | 80 | 2208,0 | 761,76 | 6400 | 28,77 |
| 4 | 16,2 | 71 | 1150,2 | 262,44 | 5041 | 20,40 |
| 5 | 29,7 | 77 | 2286,9 | 882,09 | 5929 | 25,98 |
| 6 | 26,8 | 77 | 2063,6 | 718,24 | 5929 | 25,98 |
| 7 | 30,3 | 84 | 2545,2 | 918,09 | 7056 | 32,48 |
| 8 | 15,7 | 66 | 1036,2 | 246,49 | 4356 | 15,77 |
| 9 | 25,5 | 74 | 1887,0 | 650,25 | 5476 | 23,20 |
| 10 | 15,8 | 67 | 1058,6 | 249,64 | 4489 | 16,70 |
| Всего | 236,6 | 745 | 17917,7 | 5914,00 | 55817 | 236,60 |
| В среднем | 23,66 | 74,5 | 1791,77 | 591,40 | 5581,7 | 23,66 |
Задача № 3.
По данным задачи №2 необходимо осуществить статистическую проверку существенности выборочных коэффициентов регрессии и корреляции, найти интервалы, в которых находятся их значения в генеральной совокупности. Уровень значимости ![]() .
.
Задача № 4.
По группе коров симментальской породы есть данные о возрасте и продуктивности, то есть о среднегодовом надое (табл.1). Установить формы связи между двумя признаками, определить параметры уравнения регрессии, тесноту связи.
Таблица 1
Данные для расчёта показателей корреляционной связи
| № | Суточный надой, кг | Возраст, лет | Расчётные данные | |||||
|
|
|
|
|
|
|
|
| |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 8 | 3 | ||||||
| 2 | 7 | 3 | ||||||
| 3 | 9 | 4 | ||||||
| 4 | 5 | 6 | ||||||
| 5 | 12 | 5 | ||||||
| Всего | 41 | 21 | ||||||
Тесты для закрепления материала
Тест 1
По направлению связи бывают:
а) прямыми и обратными;
б) линейными и нелинейными;
в) парными и множественными;
г) непосредственными и косвенными;
д) сильными и слабыми.
Тест 2
По аналитической форме связи бывают:
а) прямыми и обратными;
б) линейными и нелинейными;
в) парными и множественными;
г) непосредственными и косвенными;
д) сильными и слабыми.
Тест 3
Ранжированием называется:
а) возведение в квадрат коэффициента корреляции;
б) упорядочение единиц совокупности по значению признака;
в) оценка согласованности вариации взаимосвязанных признаков.
Литература:
1. Ефимова М.Р. , Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.:ИНФА-М, 2002. – 416 с.
2. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001.-320 с.
3. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
4. Статистика: Учебное пособие/Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. В.Г. Ионина. – Изд. 2-е, перераб. и доп. – М.: ИНФРА-М, 2002. – 384 с.
5. Мармоза А.Т. Практикум з основ статистики. К.: Ельга, Ніка-Центр, 2003. – 344 с.
6. Сборник задач по общей теории статистики. Учебное пособие. Изд. 2-е. /Под ред. Серга Л.К. – М.: Информационно-издательский дом «Филин», Рилант, 2001. – 360 с.
Тема 9. Анализ таблиц взаимной сопряжённости
План лекционных занятий
17. Анализ таблиц взаимной сопряжённости.
17.1. Оценка согласованности вариации атрибутивных признаков.
17.2. Коэффициенты контингенции и ассоциации.
Методические указания
Взаимосвязи между атрибутивными признаками анализируются на основе таблиц взаимной сопряжённости (взаимозависимости).
Оценка плотности стохастичной связи базируется на отклонениях частот условного и безусловного распределений, то есть на отклонениях фактических частот ![]() от теоретических
от теоретических ![]() , пропорциональных итоговым:
, пропорциональных итоговым:
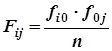 ,
,
где ![]() - итоговые частоты по признаку
- итоговые частоты по признаку ![]() ;
;
![]() - итоговые частоты по признаку
- итоговые частоты по признаку ![]() ;
;
![]() - объём совокупности (
- объём совокупности (![]() ).
).
Абсолютную величину отклонений фактических частот ![]() от пропорциональных
от пропорциональных ![]() характеризует коэффициент взаимной сопряжённости Пирсона
характеризует коэффициент взаимной сопряжённости Пирсона ![]() :
:
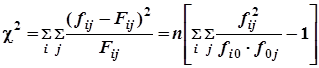 .
.
При отсутствии стохастичной связи ![]() =0. На основе распределения вероятностей
=0. На основе распределения вероятностей ![]() проверяется существенность связи.
проверяется существенность связи.
Относительной мерой плотности стохастичной связи служит коэффициент взаимной сопряжённости (взаимозависимости). Если ![]() , то использую формулу Чупрова:
, то использую формулу Чупрова:
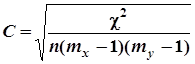 ,
,
где ![]() - число групп по признаку
- число групп по признаку ![]() ;
;
![]() - число групп по признаку
- число групп по признаку ![]() .
.
При отсутствии связи между признаками ![]() , то и
, то и ![]() . При функциональной связи
. При функциональной связи ![]() .
.
Коэффициент Чупрова даёт более осторожную оценку связи.
Когда ![]() , использую коэффициент сопряжённости Крамера:
, использую коэффициент сопряжённости Крамера:
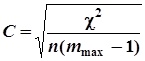 ,
,
где ![]() - минимальное число групп (
- минимальное число групп (![]() или
или ![]() ).
).
В нашем примере ![]() =3, поэтому приведённые формулы коэффициента взаимной сопряжённости тождественны:
=3, поэтому приведённые формулы коэффициента взаимной сопряжённости тождественны:
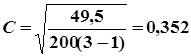 ,
,
это свидетельствует о наличии связи.
Если оба взаимосвязанных признака альтернативные, то количество групп ![]() = 2, при отсутствии связи произведения диагональных частот одинаковые:
= 2, при отсутствии связи произведения диагональных частот одинаковые: ![]() .
.
Тесноту связи между атрибутивными признаками можно измерять с помощью специальных коэффициентов ассоциации и контингенции, предложенных соответственно Д. Юлом и К. Пирсоном. Чтобы их вычислить строят 4-клеточную таблицу, которая показывает связь между двумя признаками, каждый их которых должен быть альтернативным, то есть таким, что состоит из двух качественно отличных один от другого значений (например, земли удобрены или нет).
Коэффициенты вычисляются по таким формулам:
Ассоциации
![]() ,
,
Контингенции
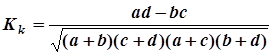 .
.
Эти коэффициенты могут быть разных значений от –1 до +1. Коэффициент контингенции всегда меньше коэффициента ассоциации. Величины этих коэффициентов как показателей тесноты связи трактуют, как и величину коэффициента корреляции.
Полезной мерой при анализе 4-клеточных таблиц взаимной сопряжённости является отношение перекрёстных произведений или отношение шансов:
![]() .
.
Отношение шансов характеризует меру относительного риска.
Следует отметить, что методы анализа таблиц взаимной сопряжённости можно использовать и для количественных признаков. Какие-либо технические преграды отсутствуют. Но следует помнить, что коэффициент сопряжённости оценивает лишь согласованность фактического распределения с пропорциональным. При переставлении столбцов или строк значение коэффициента ![]() не изменяется. Меры плотности корреляционной связи – коэффициент детерминации
не изменяется. Меры плотности корреляционной связи – коэффициент детерминации ![]() и корреляционное отношение
и корреляционное отношение ![]() - оценивают не только согласованность частот, но и порядок, последовательность, в которой объединяются разные значения признаков. То есть эти характеристики связи более мощные. А в целом выбор метода измерения связи и характеристики его плотности должен базироваться на предварительном теоретическом анализе сути явлений, характера взаимосвязи, имеющейся информации
- оценивают не только согласованность частот, но и порядок, последовательность, в которой объединяются разные значения признаков. То есть эти характеристики связи более мощные. А в целом выбор метода измерения связи и характеристики его плотности должен базироваться на предварительном теоретическом анализе сути явлений, характера взаимосвязи, имеющейся информации
Литература:
1. Ефимова М.Р. , Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.:ИНФА-М, 2002. – 416 с.
2. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001. - 320 с.
3. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
4. Статистика: Учебное пособие / Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. В.Г. Ионина. – Изд. 2-е, перераб. и доп. – М.: ИНФРА-М, 2002. – 384 с.
5. Мармоза А.Т. Практикум з основ статистики. К.: Ельга, Ніка-Центр, 2003. – 344 с.
6. Сборник задач по общей теории статистики. Учебное пособие. Изд. 2-е. /Под ред. Серга Л.К. – М.: Информационно-издательский дом «Филин», Рилант, 2001. – 360 с.
Тема 10. Анализ интенсивности динамики
План лекционных занятий18. Ряды динамики.
18.1. Классификация рядов динамики.
18.2. Характеристики интенсивности динамики.
18.3. Анализ рядов динамики.
Методические указания
Рядом динамики называется ряд статистических чисел, которые характеризуют изменения величины общественного явления во времени.
В каждом ряду динамики имеются два основных элемента:
1) показатель времени « t »;
2) уровни развития изучаемого явления «y».
В качестве показателей времени в рядах динамики выступают либо определённые даты (моменты) времени, либо отдельные периоды (сутки, месяцы, кварталы). Уровни рядов динамики отображают количественную оценку развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными и средними величинами. Динамические ряды имеют свои уровни:
- начальные;
- конечные;
- средние.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определённым датам (моментам) времени, или к отдельным периодам времени. В соответствии с этим ряды динамики подразделяются на два вида:
1. Моментный ряд – это ряд динамики, уровни которого характеризуют размеры общественно-экономических явлений по состоянию на определённый момент. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счёт.
2. Периодический (интервальный ряд) – это ряд динамики, уровни которого характеризуют размеры общественно-экономических явлений за определённые периоды времени (неделя, месяц, полугодие). Особенностью периодического ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени.
Важнейшее условие правильного построения и исследования рядов динамики – сопоставимость уровней этих рядов, относящихся к различным периодам. Сопоставимость данных статистики – это соответствие условий и методов расчёта её показателей, обеспечивающих правильность получаемых при их сравнении выводов о различиях между изучаемыми явлениями. Данное условие решается либо в процессе сбора и обработки данных, либо путём их пересчёта. Соблюдение требований к сопоставимости уровней ряда означает, что научно обоснованным будет такое сравнение, которое учитывает существо изучаемого явления и цель, к которым оно приводится.
Требования к сопоставимости показателей динамического ряда:
1. Все показатели РД должны быть достоверными, точными, научно обоснованными.
2. Интервалы времени должны быть сходны в экономическом отношении. Например, объём производства зерна за различные годы следует сравнивать только за определенный месяц.
3. Единицы измерения должны быть единые. Например, только литры или только килограммы.
4. Показатели должны иметь одну и ту же полноту охвата исследуемых объектов, то есть должны быть сопоставимы по составу.
5. Уровни РД должны иметь единые способы исчисления, например, численность работающих исчислена на начало каждого года, а по другим годам – как среднегодовая численность. Такие РД непригодны.
6. Показатели РД должны быть сопоставимы по территории, к которым они относятся. Например, изменение границ и численность населения.
В статистике для того, чтобы выявить особенности развития изучаемых явлений и процессов за отдельные периоды времени, исчисляются абсолютные и относительные показатели изменения ряда динамики:
1) абсолютный прирост.
2) средний абсолютный прирост.
3) абсолютное значение одного процента прироста.
4) темп роста.
5) темп прироста.
6) средний темп роста.
7) средний темп прироста.
В основе расчёта показателей РД лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной или переменной базах сравнения.
Для расчёта показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисленные при этом показатели считаются базисными. Для расчёта показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными.
1. Абсолютный прирост (![]() ) – это разность между уровнями данного периода и периода, принятого за базу сравнения (предыдущего периода). Он вычисляется по формулам:
) – это разность между уровнями данного периода и периода, принятого за базу сравнения (предыдущего периода). Он вычисляется по формулам:
а) базисный ![]()
б) цепной ![]()
![]() - абсолютный прирост базисный.
- абсолютный прирост базисный.
![]() - абсолютный прирост цепной.
- абсолютный прирост цепной.
![]() - сравниваемый уровень.
- сравниваемый уровень.
![]() - уровень периода, взятого за базу.
- уровень периода, взятого за базу.
![]() - уровень, предшествующий сравниваемому периоду.
- уровень, предшествующий сравниваемому периоду.
2. Средний абсолютный прирост представляет собой обобщённую характеристику индивидуальных абсолютных приростов ряда динамики. Он определяется по формулам:
![]() или
или ![]() ,
,
где ![]() - число показателей в периоде.
- число показателей в периоде.
3. Абсолютное значение одного процента прироста (А) характеризует абсолютный эквивалент одного процента прироста и определяется по формуле:
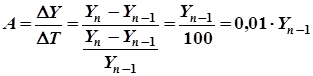 ,
,
где ![]() - абсолютный цепной прирост.
- абсолютный цепной прирост.
![]() - темп прироста, %.
- темп прироста, %.
4. Темп роста (Т) характеризует средний относительный рост явления за рассматриваемый период. Рассчитывается по формуле:
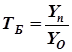 ;
; 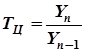 .
.
5. Темп прироста (![]() ) характеризует относительный прирост явления в отчётном периоде по сравнению с тем уровнем, с которым осуществляется сравнение. Он определяется по формулам:
) характеризует относительный прирост явления в отчётном периоде по сравнению с тем уровнем, с которым осуществляется сравнение. Он определяется по формулам:
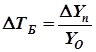 ;
; 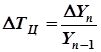
Или
![]()
![]()
6. Средний темп роста (![]() ) определяют по формуле средней геометрической двумя способами: на основе данных цепных коэффициентов динамики, либо на основе абсолютных уровней ряда динамики по формулам:
) определяют по формуле средней геометрической двумя способами: на основе данных цепных коэффициентов динамики, либо на основе абсолютных уровней ряда динамики по формулам:
![]() или
или 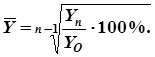
7. Средний темп прироста (![]() ) определяется на основе взаимосвязи между темпами роста и прироста:
) определяется на основе взаимосвязи между темпами роста и прироста:
![]() .
.
В моментных рядах динамики средние уровни вычисляются двумя способами:
а) если моментный ряд динамики имеет равные промежутки времени между двумя составными датами, то средний уровень вычисляется по формуле средней хронологической:
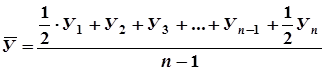 ,
,
где ![]() - средний уровень ряда динамики;
- средний уровень ряда динамики;
![]() - абсолютные уровни ряда динамики;
- абсолютные уровни ряда динамики;
![]() - число абсолютных ровней.
- число абсолютных ровней.
б) если моментный ряд динамики имеет неодинаковые промежутки времени между двумя составными датами, то средний уровень вычисляется по формуле средней взвешенной по времени:
![]() ,
,
где ![]() - средний уровень ряда динамики;
- средний уровень ряда динамики;
![]() - абсолютные уровни ряда динамики;
- абсолютные уровни ряда динамики;
![]() - периоды времени между датами.
- периоды времени между датами.
Средние уровни в периодических рядах динамики исчисляются как простая средняя арифметическая, то есть путём деления суммы всех уровней на их количество.
в) для приблизительной оценки среднего уровня иногда определяют полусумму на начало и конец периода и принимают её за характеристику среднего уровня всего периода. Однако этот средний уровень является приблизительной оценкой, его применяют нечасто, так как не учитываются промежуточные значения ряда динамики.
![]() ,
,
В периодических рядах динамики средние уровни исчисляются как простая арифметическая, то есть путём деления суммы всех уровней на их количество:
![]() .
.
Решение типовых задач
Задача № 1.
Известны следующие данные выполнения экономической программы предприятием за отчетный год, тыс. грн. Требуется произвести укрупнение ряда.
Таблица 1
| Месяцы | Выпуск продукции, тыс. грн. | Месяцы | Выпуск продукции, тыс. грн. |
| Январь | 20,2 | Июль | 18,4 |
| Февраль | 18,8 | Август | 16,6 |
| Март | 22,4 | Сентябрь | 20,2 |
| Апрель | 20,0 | Октябрь | 20,8 |
| Май | 17,8 | Ноябрь | 22,4 |
| Июнь | 18,6 | Декабрь | 22,0 |
Ход решения.
у1 = 20,2 + 18,8 + 22,4 = 61,4
у2 = 20,0 + 17,8 + 18,6 = 56,4
у3 = 18,4 + 16,6 + 20,2 = 55,2
у4 = 20,8 + 22,4 + 22,0 = 65,2
Выровненный ряд динамики имеет вид:
61,4; 56,4; 55,2; 65,2.
То есть, наблюдается четко выраженная тенденция увеличения выпуска продукции в I и IV кварталах отчетного года.
Задача №2.
По нижеприведённым данным (в тыс. грн) о кредитных вложениях украинских банков в 2002 г. рассчитайте:
1) средний уровень каждого ряда;
2) среднегодовой темп роста вложений всего и в том числе по видам;
3) сопоставьте, определите коэффициенты опережения и замедления.
Таблица 1
| 01.01.02 | 01.04.02 | 01.07.02 | 01.10.02 | 01.01.03 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| Кредитные вложения, | 1216,5 | 1331,9 | 1360,5 | 1532,2 | 1397,5 |
| в т. ч. краткосрочные, | 1194,7 | 1268,4 | 1324,3 | 1493,0 | 1359,1 |
| долгосрочные | 21,8 | 63,5 | 36,3 | 39,2 | 38,4 |
Ход решения:
1. Средний уровень каждого ряда определяем по формуле средней хронологической простой (т. к. ряд динамики моментный):
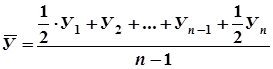 ;
;
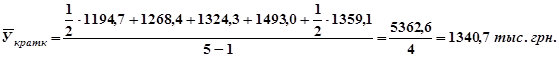
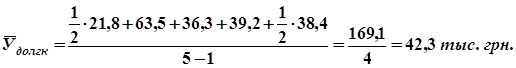
2. Среднегодовой темп роста вложений определяем по формуле:
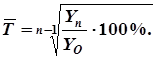
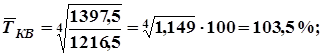
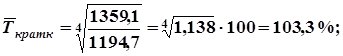
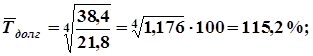
3. Коэффициент опережения темпа роста долгосрочных вложений над темпом роста краткосрочных вложений:
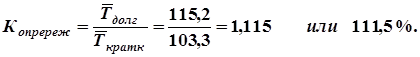
Задачи для самостоятельного выполнения
Задача №3.
Ежегодный прирост продукции фирмы характеризуется следующими данными (в % к предшествующему году):
| 1998 | 1999 | 2000 | 2001 | 2002 |
| 11 | 9 | 12 | 14 | 17 |
Определите относительное изменение в выпуске продукции фирмы за весь изучаемый период и в среднем за год.
Задача № 4.
Провести анализ динамики продажи мясных консервов за 1998-2002 гг. Исходные данные и расчётные показатели изложены в табл.1.
Таблица 1
Динамики продажи мясных консервов в регионе и расчёт аналитических показателей динамики (данные условные)
| Исходные данные | Расчётные показатели | |||||||
| Годы | Консервы, млн. усл. банок | Абсолютные приросты (снижение), млн. усл. банок | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1 % прироста, млн. усл. банок | |||
| цеп. | баз. | цеп. | баз. | цеп. | баз. | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1998 | 891 | - | - | - | 100,0 | - | 0,0 | - |
| 1999 | 806 | -85 | -85 | 90,5 | 90,5 | -9,5 | -9,5 | 8,9 |
| 2000 | 1595 | +789 | +704 | 197,9 | 179,0 | 97,9 | 79,0 | 8,06 |
| 2001 | 1637 | +42 | +746 | 102,6 | 183,7 | 2,6 | 83,7 | 15,95 |
| 2002 | 1651 | +14 | +760 | 100,8 | 185,3 | 0,8 | 85,3 | 16,37 |
| Итого | 6580 | +760 | - | - | - | - | - | - |
Задача № 5.
Имеются следующие данные о производстве зерна.
Таблица 1| Годы | 1998 | 1999 | 2000 | 2001 | 2002 |
| Производство зерна, тыс. т | 150 | 168 | 179 | 186 | 191 |
Требуется определить:
а) абсолютный прирост;
б) темп роста и прироста;
в) абсолютное значение 1% прироста;
г) средний абсолютный прирост;
д) среднегодовой темп роста и прироста.
Тесты для закрепления материала Тест 1 Абсолютный прирост вычисляется как: а) отношение уровней ряда динамики;б) разница между уровнями ряда динамики.
Тест 2
Темпы динамики вычисляются как:
а) отношение уровней ряда динамики;
б) разница между уровнями ряда динамики.
Тест 3
Темпы прироста вычисляются как:
а) разница между уровнями ряда динамики;
б) отношение абсолютного прироста к уровню ряда, взятого за базу сравнения;
в) отношение абсолютного прироста к темпу динамики;
г) отношение уровней ряда динамики.
Тест 4
Абсолютное значение 1 % прироста исчисляется или равно:
а) одному проценту уровня, взятого за базу сравнения;
б) абсолютному приросту, разделённому на темп прироста;
в) уровню ряда динамики, разделённому на темп прироста;
г) абсолютному приросту, разделённому на темп динамики.
Литература
1. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001. - 320 с.
2. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
3. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. О.Э. Башиной, А.А. Спирина. – 5-е изд., доп. и перераб. – М.: Финансы и статистика, 1999. – 440 с.
4. Захожай В.Б., Попов І.І., Коваленко О.В. Практикум з основ статистики: Навч. посіб. – К.: МАУП, 2001.- 176 с.
Тема 11. Анализ тенденций развития
План лекционных занятий
19. Анализ тенденций развития.
19.1. Характеристика основной тенденции развития.
19.2. Измерение сезонных колебаний.
Методические указания
Один из важнейших вопросов, возникающих при изучении рядов динамики – это выявление тенденции развития экономического явления в динамике. Какой-либо динамический ряд в пределах периода с более-менее стабильными условиями развития проявляет определённую закономерность изменения уровней – общую тенденцию. Одним рядам присуща тенденция роста, другим – снижение уровней. Возрастание или снижение уровней ряда, в свою очередь, происходит по-разному: равномерно, ускоренно или замедленно. Нередко ряды динамики через колебание уровней не проявляют чёткой выраженной тенденции.
Для выявления и характеристики применяют такие методы:
- метод укрупнения периодов;
- метод скользящей средней;
- метод аналитического выравнивания.
1. Метод укрупнения периодов – заключается в том, что уровни исходного динамического ряда объединяются по более крупным периодам. Например, сравнивают уровни урожайности не за отдельные годы, а в среднем по пятилеткам. Особое внимание при этом следует обращать на обоснование периодов укрупнения.
2. Метод скользящей средней заключается в замене первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня с постепенным включением последующих уровней, то есть при расчёте каждого последующего сглаженного уровня принятый для укрупнения период сдвигается на одну дату. Например при сглаживании по трёхлетиям:
![]()
3. Метод аналитического выравнивания является наиболее совершенным методом выявления тенденции ряда динамики. Сущность его заключается в том, что подбирается уравнение (трендовое уравнение), которое наиболее полно отражает характер изменения динамического ряда за изучаемый период. Таким уравнением, в частности, может быть уравнение прямой линии:
![]() ,
,
где ![]() - параметры прямой, (начальный уровень и ежегодный прирост), их нужно определять.
- параметры прямой, (начальный уровень и ежегодный прирост), их нужно определять.
![]() - время.
- время.
Для нахождения ![]() нужно решить систему уравнений по способу наименьших квадратов:
нужно решить систему уравнений по способу наименьших квадратов:
 .
.
Продолжение выявленной тенденции за пределы ряда динамики называют экстраполяцией тренда. Это один из методов статистического прогнозирования, предпосылкой использования которого является неизменность причинного комплекса, который формирует тенденцию.
Самой простой оценкой систематических колебаний являются коэффициенты неравномерности, которые вычисляются как отношение максимального и минимального уровней динамического ряда к среднему. Чем больше неравномерность процесса, тем больше разница между двумя этими коэффициентами.
Сезонными колебаниями называют более-менее стойкие внутригодовые колебания в рядах динамики, обусловленные специфическими условиями производства или потребления определённого вида продукции. Сезонные колебания характеризуются специальным показателем, который называется индексом сезонности ![]() . В совокупности эти индексы образуют сезонную волну.
. В совокупности эти индексы образуют сезонную волну.
Индекс сезонности – это процентное отношение одноимённых месячных (квартальных) фактических уровней рядов динамики к их среднегодовым или выровненным уровням.
Решение типовых задач
Задача № 1.
Имеются следующие данные об отпуске электроэнергии (табл. 1). Необходимо выявить сезонную волну.
Ход решения:
Для выделения сезонной волны надо определить средний уровень отпуска энергии за каждый месяц по трёхлетним данным (5 строка тал.1) и общую среднюю за весь рассматриваемый период. Например, средний уровень за январь получим делением суммы уровней на число лет:
![]()
Общая средняя ![]() получается делением суммы уровней отпуска за все три года на 36 (общее число месяцев), то есть
получается делением суммы уровней отпуска за все три года на 36 (общее число месяцев), то есть
![]() .
.
Затем определяется абсолютное отклонение средних месячных показателей от общей средней ![]() (строка 6). Например, за январь абсолютное отклонение составило 2,5 млн. кВт-ч (132,9-130,4). Аналогичные расчёты сделаны для всех остальных месяцев.
(строка 6). Например, за январь абсолютное отклонение составило 2,5 млн. кВт-ч (132,9-130,4). Аналогичные расчёты сделаны для всех остальных месяцев.
Метод относительных разностей является развитием метода абсолютных разностей. Для нахождения относительных разностей абсолютные отклонения делят на общую среднюю и выражают в процентах (строка 7). Например, за январь: 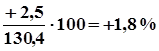 .
.
Вместо относительных разностей за каждый месяц может быть вычислен индекс сезонности, который рассчитывается как отношение среднего уровня соответствующего месяца к общей средней. Значения индексов сезонности представлены в строке 8.
Данные об отпуске электроэнергии за 2000 – 2002 гг. (млн. кВт-ч)
Таблица 1| Итого за все месяцы | |||||||||||||
| Год | январь | февраль | март | апрель | май | июнь | июль | август | сент. | октябрь | нояб. | дек. | |
| 1. 2000 | 126,5 | 119,4 | 114,2 | 100,0 | 80,8 | 89,1 | 96,1 | 104,4 | 114,1 | 133,0 | 123,1 | 145,0 | 1325,7 |
| 2. 2001 | 138,7 | 135,5 | 133,8 | 130,5 | 104,8 | 111,8 | 112,6 | 134,2 | 137,9 | 133,6 | 131,1 | 147,3 | 1551,8 |
| 3. 2002 | 133,6 | 133,4 | 131,6 | 119,0 | 91,9 | 108,3 | 169,9 | 188,2 | 190,4 | 194,1 | 156,5 | 178,7 | 1795,6 |
| 4. Итого за весь период | 398,8 | 389,3 | 379,6 | 349,5 | 277,5 | 309,2 | 378,6 | 426,8 | 442,4 | 460,7 | 410,7 | 471,0 | 4694,1 |
| 5. Средний уровень за месяц | 132,9 | 129,8 | 126,5 | 116,5 | 92,5 | 103,1 | 126,2 | 142,3 | 147,5 | 153,6 | 136,9 | 157,0 | 130,4 |
| 6. Абсолютное отклонение от общей средней | +2,5 | -0,6 | -3,9 | -13,9 | -37,9 | -27,3 | -4,2 | +31,9 | +17,1 | +23,2 | +6,5 | +26,6 | |
| 7. Относительное отклонение от общей средней (в %) | +1,9 | -0,5 | -3,0 | -10,7 | -29,1 | -20,9 | -3,2 | +9,1 | +13,1 | +117,8 | +5,0 | +20,4 | |
| 8. Индекс сезонности:
| 101,9 | 99,5 | 97,0 | 89,3 | 70,9 | 79,1 | 96,8 | 109,1 | 113,1 | 117,8 | +105,0 | 120,4 | |
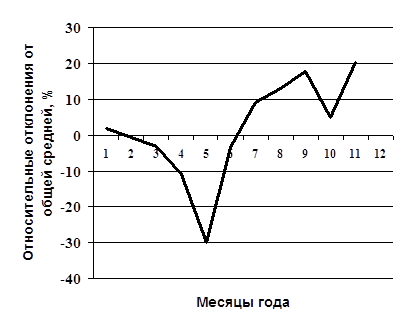
Рис. 1. Относительные отклонения объёма производства электроэнергии по месяцам (в % от общей средней месячной)
Вывод: На рис.1 сезонная волна выглядит достаточно отчётливо.
Задания для самостоятельного выполнения
Задача № 2.
Имеются данные об изменении объёмов промышленного производства:
| Месяц | Темп роста общего объема производства в % к декабрю 2000 г. | |
| 2001 г. | 2002 г. | |
| 1 | 2 | 3 |
| Январь | 92,0 | 86,0 |
| Февраль | 90,5 | 86,2 |
| Март | 95,0 | 91,0 |
| Апрель | 88,2 | 88,2 |
| Май | 89,0 | 84,0 |
| Июнь | 90,7 | 83,8 |
| Июль | 89,3 | 83,9 |
| Август | 93,0 | 84,2 |
| Сентябрь | 92,6 | 85,0 |
| Октябрь | 94,9 | 89,8 |
| Ноябрь | 91,8 | 86,3 |
| Декабрь | 92,2 | 87,1 |
Проанализируйте сезонные изменения промышленного производства:
1) на основе индекса сезонности;
2) применяя графический метод.
Задача №3.
Имеются данные по предприятию о динамике производства молока за три года (табл.1). Необходимо проанализировать сезонность производства молока.
Таблица 1
| Месяц | Год | Всего за три года | В среднем за три года | Показатели сезонности | ||
| 2000 | 2001 | 2002 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| I | 120 | 131 | 112 | 363 | 121,0 | 78,7 |
| II | 125 | 127 | 130 | 382 | 127,3 | 82,8 |
| III | 140 | 152 | 143 | 435 | 145,0 | 94,3 |
| IV | 157 | 160 | 162 | 479 | 159,7 | 103,8 |
| V | 168 | 181 | 175 | 524 | 174,7 | 113,6 |
| VI | 181 | 194 | 197 | 572 | 190,7 | 124,0 |
| VII | 196 | 201 | 191 | 588 | 196,0 | 127,4 |
| VIII | 183 | 180 | 171 | 534 | 178,0 | 115,7 |
| IX | 160 | 165 | 154 | 479 | 159,7 | 103,8 |
| X | 142 | 148 | 155 | 445 | 148,3 | 96,4 |
| XI | 133 | 127 | 140 | 400 | 133,3 | 86,7 |
| XII | 115 | 110 | 111 | 336 | 112,0 | 72,8 |
| Всего | 1820 | 1876 | 1841 | 5537 | 153,8 | 1200,0 |
| В среднем | 151,7 | 156,3 | 153,4 | 461,4 | 153,8 | 100,0 |
Задача №4.
Имеются данные о динамике использования трудовых ресурсов в области по месяцам года (табл.1). Необходимо проанализировать сезонность этого явления.
Таблица 1
| № вар-та | Месяц | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 681 | 677 | 650 | 894 | 720 | 985 | 1086 | 931 | 912 | 806 | 752 | 815 |
| 2 | 378 | 360 | 385 | 392 | 428 | 462 | 427 | 574 | 446 | 397 | 437 | 370 |
| 3 | 348 | 383 | 446 | 346 | 512 | 714 | 603 | 534 | 509 | 499 | 406 | 399 |
| 4 | 530 | 608 | 651 | 668 | 646 | 871 | 856 | 801 | 674 | 866 | 607 | 504 |
| 5 | 885 | 841 | 1002 | 999 | 1038 | 1219 | 1382 | 1182 | 975 | 1675 | 1251 | 744 |
Сезонными колебаниями называют:
а) отношение максимального и минимального уровней динамического ряда к среднему;
б) более-менее стойкие внутригодовые колебания в рядах динамики, обусловленные специфическими условиями производства или потребления определённого вида продукции;
в) уровни исходного динамического ряда объединяются по более крупным периодам.
Тест 2Метод аналитического выравнивания подразумевает:
а) уровни исходного динамического ряда объединяются по более крупным периодам;
б) замену первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня с постепенным включением последующих уровней;
в) подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период.
Тест 3 Метод укрупнения периодов подразумевает:а) уровни исходного динамического ряда объединяются по более крупным периодам;
б) замену первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня с постепенным включением последующих уровней;
в) подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период.
Тест 4Метод скользящей средней подразумевает:
а) уровни исходного динамического ряда объединяются по более крупным периодам;
б) замену первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня с постепенным включением последующих уровней;
в) подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период.
Литература:
1. Ефимова М.Р. , Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.:ИНФА-М, 2002. – 416 с.
2. Теорія статистики: Навчальний посібник / Вашків П.Г., Пастер П.Ш., Сторожук В.П., Ткач Є.Ш. – К.: Либідь, 2001. - 320 с.
3. Статистика: Підручник / С.С. Герасименко, А.В. Головач та ін. 2-е вид., перероб. і доп. – К. : КНЕУ, 2000. – 467 с.
4. Статистика: Учебное пособие / Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. В.Г. Ионина. – Изд. 2-е, перераб. и доп. – М.: ИНФРА-М, 2002. – 384 с.
5. Мармоза А.Т. Практикум з основ статистики. К.: Ельга, Ніка-Центр, 2003. – 344 с.
6. Сборник задач по общей теории статистики. Учебное пособие. Изд. 2-е. /Под ред. Серга Л.К. – М.: Информационно-издательский дом «Филин», Рилант, 2001. – 360 с.
Тема 12. Экономические индексы
План лекционных занятий20. Индексный метод в статистике.
20.1. Общее понятие об индексах.
20.2. Виды индексов.
20.3. Использование индивидуальных индексов в экономическом анализе.
21. Агрегатные индексы.
21.1. Формы представления общих индексов.
21.2. Средний гармонический и средний арифметический индексы.
22. Взаимосвязь индексов.
22.1. Взаимосвязь индексов.
22.2. Территориальные индексы.
23. Использование индексов в экономическом анализе.
23.1. Индекс структурных сдвигов.
23.2. Использование индексов в макроэкономическом анализе.
Методические указания
В статистических исследованиях для характеристики социально-экономических явлений и процессов широко используют обобщающие показатели в виде средних, относительных и других величин. К этим характеристикам относятся и индексы, занимающие особенное место среди статистических показателей. В переводе с лат. «INDEX» означает «показатель», но именно в статистике он имеет специфическое значение. Каждый индекс является соотношением двух значений показателя, который индексируется: оценочного (текущего) и взятого за базу сравнения. То есть по статистической природе индекс – это относительная величина, которая характеризует изменение социально-экономического явления во времени (индексы динамики), в пространстве (территориальные индексы) или степень отклонения значений показателя от определённого стандарта (планового показателя, договорных обязательств, средней величины). Формы выражения индекса: коэффициенты, проценты, промилле. Однако индексом не стоит считать какую-либо относительную величину сравнения, с помощью которой характеризуют изменение сложных социальных явлений.
Статистический индекс – это обобщающий показатель, который выражает соотношение величин сложного экономического явления, состоящего из элементов непосредственно несуммируемых.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... распределения генеральной совокупности F(x) и – эмпирической функция распределения Fn(x) , построенной по выборке х1,…,хn, называется функция. Теорема. Если F(x) непрерывна, то распределения статистики Колмогорова Dn не зависит от F(x). Условные математические ожидания и условные распределения. Св-ва условных мат. ожиданий. Аналоги формул полной вероятности и формулы Байеса для мат. ожиданий ГММЕ ...
... дает возможность статистического моделирования, происходящих в населении процессов. Потребность в моделировании возникает в случае невозможности исследования самого объекта. Наибольшее число моделей, применяемых в статистике населения, разработано для характеристики его динамики. Среди них выделяются экспоненциальные и логистические. Особое значение в прогнозе населения на будущие периоды имеют ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
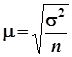
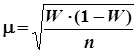
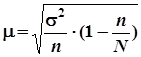
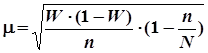
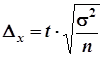
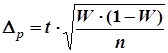
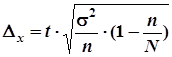
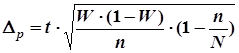
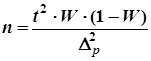
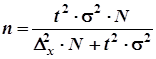
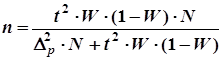
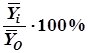
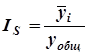










0 комментариев