Навигация
Вычислим среднюю арифметическую по исходным данным
4. Вычислим среднюю арифметическую по исходным данным.
![]() = 173 чел.
= 173 чел.
Результат расчетов средней арифметической в п.3 совпадает с результатом расчетов в п.4. Это произошло потому, что при исчислении средней арифметической в интервальном ряде допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале. Т.к. интервал в нашей задаче достаточно узкий - 20, а число единиц в интервале достаточно большое, следовательно, ошибка расчетов в п.3 мала, и результаты расчетов п.3 и п.4 совпадают.
ЗАДАНИЕ 2
По исходным данным:
1. Установите наличие и характер связи между признаками среднесписочная численность работников (х – факторный) и выпуском продукции (y - результативный), образовав 5 групп по обоим признакам с равными интервалами, методами:
· аналитической группировки:
· корреляционной таблицы.
2. Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения.
Сделайте выводы по результатам выполненного задания.
РЕШЕНИЕ
1. Аналитическая группировка.
· Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в каждой из образованных групп, определение объема варьирующих признаков в пределах созданных групп, а также исчисление средних размеров результативного показателя. Результаты группировки оформляются в таблице. Установим наличие и характер связи между величиной среднесписочной численности работников и выпуском продукции методом аналитической группировки по данным таблицы исходных данных.
Вначале строим рабочую таблицу (табл.2.1).
Таблица 2.1.
Распределение предприятий по среднесписочной численности работников.
| № п.п | Группы предприятий по среднесписочной численности работников | № пред- прия- тия | Среднесписочная численность работников, чел. | Объем выпускаемой продукции, млн.руб. |
| А | Б | 1 | 2 | 3 |
| I | 120 – 140 | 11 23 16 | 120 130 137 | 24 14 25 |
| Итого | 3 | 387 | 63 | |
| II | 140 - 160 | 15 19 12 22 1 | 142 145 148 156 159 | 30 28 36 34 37 |
| Итого | 5 | 750 | 165 | |
| III | 160 - 180 | 3 18 14 9 21 24 17 2 25 29 10 | 161 163 165 169 166 170 171 174 175 177 179 | 40 41 42 43 39 46 45 47 48 45 48 |
| Итого | 11 | 1870 | 484 | |
| IV | 180 - 200 | 5 26 8 28 13 30 4 | 182 184 187 189 190 194 197 | 44 54 59 56 58 61 60 |
| Итого | 7 | 1323 | 392 | |
| А | Б | 1 | 2 | 3 |
| V | 200 - 220 | 20 7 27 6 | 208 215 217 220 | 70 68 74 64 |
| Итого | 4 | 860 | 276 | |
| Всего | 30 | 5190 | 1380 | |
Для установления наличия и характера связи между величиной среднесписочной численности работников и объемом выпускаемой продукции по данным рабочей таблицы 2.1 строим итоговую аналитическую таблицу 2.2.
Таблица 2.2.
Зависимость объема выпускаемой продукции от среднесписочной численности работников.
| № п.п. | Группы предприятий по среднесписочной численности работников | Число пред –приятий | Среднесписочная численность работников | Объем выпускаемой продукции | ||
| Всего | Средняя численность работников | Всего | в среднем на одно предприятие | |||
| А | Б | 1 | 2 | 3 | 4 | 5 |
| 120 – 140 140 – 160 160 – 180 180 – 200 200 – 220 | 3 5 11 7 4 | 387 750 1870 1323 860 | 129 150 170 189 215 | 63 165 484 392 276 | 21 33 44 56 69 | |
| Итого | 30 | 5190 | 173 | 1380 | 46 | |
Данные таблицы 2.2 показывают, что с ростом среднесписочной численности работников, средний объем продукции, выпускаемой одним предприятием, растет. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость.
· Корреляционная таблица.
Для изучения структуры предприятий по объему выпускаемой продукции, пользуясь таблицей исходных данных, построим интервальный вариационный ряд, характеризующий распределение предприятий по объему выпускаемой продукции. Величина интервала равна:
Похожие работы
... данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и ...
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...





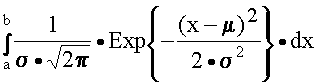
0 комментариев