Млн.руб

12 млн.руб.

Интервальный ряд	Дискретный ряд	- количество предприятий внутри i – той группы
1гр.: 14 – 26	(14+26)/2=20	3
2гр.: 26 – 38	(26+38)/2=32	5
3гр.: 38 – 50	(28+50)/2=44	12
4гр.: 50 – 62	(50+62)/2=56	6
5гр.: 62 – 74	(62+74)/2=68	4

По таблице исходных данных необходимо определить, существует ли зависимость между среднесписочной численностью работников (факторный признак х) и выпускаемой продукцией (результативный признак y).

Построим корреляционную таблицу, образовав 5 групп по факторному и результативному признакам (табл.2.3).

Таблица 2.3.

Распределение предприятий по среднесписочной численности работников и объему выпускаемой прдукции.

Среднесписочная численность работников	Выпускаемая продукция, млн.руб.
	14 – 26	26 – 38	38 – 50	50 – 62	62 – 74	Итого
120 – 140	3					3
140 – 160		5				5
160 – 180			11			11
180 – 200			1	6		7
200 – 220					4	4
Итого	3	5	12	6	4	30

 

Как видно из данных табл.2.3, распределение числа предприятий произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, т.е. увеличение признак “среднесписочная численность работников” сопровождалось увеличением признака “выпускаемая продукция”.

Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.

2. Теснота корреляционной связи между названными признаками может быть измерена с помощью коэффициента детерминации и эмпирического корреляционного отношения.

·     Коэффициент детерминации равен отношению межгрупповой дисперсии к общей:

 

 

Межгрупповая дисперсия равна:

=

 

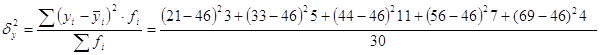Общая дисперсия равна:

=249 + 186 = 435

 

Средняя из групповых дисперсий:

==

 

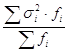Групповая дисперсия равна:

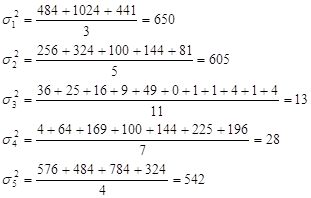
=0.428 или 42,8%

Это означает, что выпускаемая продукция на 42,8% зависит от среднесписочной численности работников, а на 57,2% - от других факторов.

·     Эмпирическое корреляционное отношение.

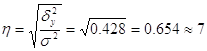
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.

В нашем примере , что свидетельствует (из соотношения Чэддока) о тесной связи (0,7 – 0,9) между выпуском продукции и среднесписочной численностью работников.

ЗАДАНИЕ 3

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1.   Ошибку выборки среднесписочной численности работников и границы, в которых будет находиться среднесписочная численность работников в генеральной совокупности.

2.   Ошибку выборки доли предприятия со среднесписочной численностью работников 180 и более человек и границы, в которых будет находиться генеральная доля.

РЕШЕНИЕ

1. Для определения среднесписочной численности работников на предприятиях была произведена 20% - ная механическая выборка, в которую попало 30 предприятий. В результате обследования было установлено, что средняя арифметическая среднесписочной численности работников 173 чел. При среднем квадратическом отклонении 23 чел.

Границы, в которых будет находиться среднесписочная численность работников в генеральной совокупности

Т.к. выборка механическая, предельная ошибка выборки определяется по формулам:

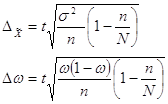
где N – объем генеральной совокупности (число входящих в нее единиц). Т.к. выборка 20% - ная, то N=150 (5*30).

20% - ная выборка означает, что отбирается и проверяется каждая 5-ая единица (1:0,2).

n – объем выборки (число обследованных единиц) = 30 предприятий.

- генеральная дисперсия (дисперсия признака в генеральной совокупности).

t = 1 (из таблицы значений интегральной функции Лапласа при заданной вероятности 0,683)

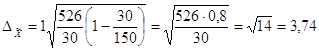
чел.

С вероятностью 0,683 можно утверждать, что среднесписочная численность работников находится в пределах или

2. Доля предприятий со среднесписочной численностью работников 180 и более человек находится в пределах:

Выборочная доля составит:

=11/30=0,37,

где m – доля единиц, обладающих признаком;

n – численность выборки.

Ошибка выборки генеральной доли составит:

 или 7,9%

С вероятностью 0,683 можно утверждать, что доля предприятий со среднесписочной численностью работников 180 чел. и более будет находиться в пределах p = 37%7.9% или 29,1%p44,9%.

ЗАДАНИЕ 4

Имеются следующие данные по двум предприятиям отрасли:

№ пр – я п/п	Выпуск продукции, тыс.руб.		Среднесписочная численность рабочих, чел.
	Базисный период	Отчетный период	Базисный период	Отчетный период
1 2	6400 4800	6000 6000	100 60	80 60

Определите:

1.   По каждому предприятию уровни и динамику производительности труда. Результаты расчетов представьте в таблице.

2.   По двум предприятиям вместе:

·     индексы производительности труда (переменного, постоянного состава, структурных сдвигов);

·     абсолютное изменение средней производительности труда за счет отдельных факторов.

Сделайте выводы.

РЕШЕНИЕ