Навигация
Проведем аналитическую группировку по РФ
3. Проведем аналитическую группировку по РФ.
Аналитическая группировка – это группировка, выявляющая взаимо-связи между отдельными признаками изучаемого явления.
хmin = 367,3 (руб.),
хmax = 6859,1 (руб.).
Так как признак количественный непрерывный, то определим число групп по формуле Стерджесса: к = 1+3,32lg n
n = 69,
к = 1+3,32lg 69 = 15;
- шаг интервала:
6859,1-367,3 6491,8
h = = = 432,8 (руб.);
15 15
- рассчитываем интервалы:
| 367,2 – 800,0 |
| 800,0 – 1232,8 |
| 1232,8 – 1665,6 |
| 1665,6 – 2098,4 |
| 2098,4 – 2531,2 |
| 2531,2 – 2964,0 |
| 2964,0 – 3396,8 |
| 3396,8 – 3829,6 |
| 3829,6 – 4262,4 |
| 4262,4 – 4695,2 |
| 4695,2 – 5128,0 |
| 5128,0 – 5560,8 |
| 5560,8 – 5993,6 |
| 5993,6 – 6426,4 |
| 6426,4 – 6859,2 |
- ранжируем данные:
| 367,3 | 785,0 | 928,7 | 1033,6 | 1087,3 | 1264,5 | 1654,4 |
| 579,0 | 819,6 | 934,3 | 1047,3 | 1113,0 | 1268,8 | 1681,8 |
| 597,0 | 825,6 | 935,1 | 1060,5 | 1161,0 | 1271,2 | 1694,9 |
| 649,9 | 846,9 | 936,5 | 1066,4 | 1162,4 | 1295,0 | 1804,0 |
| 696,1 | 852,0 | 936,8 | 1068,5 | 1187,1 | 1329,9 | 1962,1 |
| 710,7 | 865,7 | 974,4 | 1073,9 | 1197,3 | 1336,7 | 2058,0 |
| 751,5 | 869,8 | 1009,3 | 1077,5 | 1204,1 | 1458,1 | 2392,7 |
| 763,9 | 879,7 | 1013,9 | 1083,7 | 1221,7 | 1480,1 | 3266,0 |
| 767,3 | 888,0 | 1022,4 | 1083,8 | 1243,7 | 1500,5 | 6859,1 |
| 771,1 | 919,2 | 1023,6 | 1086,6 | 1246,9 | 1575,9 |
- строим статистический вариационный ряд (см. таблицу 4):
Таблица 4
Статистический вариационный ряд по РФ
| № | Интервалы | Середина | Частоты | Частости | Кумулятивная |
| интервала | частота | ||||
| ai - bi | xi | ni | Wi | ∑ni | |
| 1 | 367,2 - 800,0 | 583,6 | 11 | 0,16 | 11 |
| 2 | 800,0 - 1232,8 | 1016,4 | 37 | 0,54 | 48 |
| 3 | 1232,8 - 1665,6 | 1449,2 | 13 | 0,19 | 61 |
| 4 | 1665,6 - 2098,4 | 1882,0 | 5 | 0,08 | 66 |
| 5 | 2098,4 - 2531,2 | 2314,8 | 1 | 0,01 | 67 |
| 6 | 2531,2 - 2964,0 | 2747,6 | - | - | 67 |
| 7 | 2964,0 - 3396,8 | 3180,4 | 1 | 0,01 | 68 |
| 8 | 3396,8 - 3829,6 | 3613,2 | - | - | 68 |
| 9 | 3829,6 - 4262,4 | 4046,0 | - | - | 68 |
| 10 | 4262,4 - 4695,2 | 4478,8 | - | - | 68 |
| 11 | 4695,2 - 5128,0 | 4911,6 | - | - | 68 |
| 12 | 5128,0 - 5560,8 | 5344,4 | - | - | 68 |
| 13 | 5560,8 - 5993,6 | 5777,2 | - | - | 68 |
| 14 | 5993,6 - 6426,4 | 6210,0 | - | - | 68 |
| 15 | 6426,4 - 6859,2 | 6642,8 | 1 | 0,01 | 69 |
| ∑ | — | — | 69 | 1,00 | — |
- середина интервала:
ai + bi
xi = ,
2
367,2 + 800,0
x1 = = 583,6,
2
800,0 + 1232,8
x2 = = 1016,4,
2
1232,8 + 1665,6
x3 = = 1449,2,
2
1665,6 + 2098,4
x4 = = 1882,0,
2
2098,4 + 2531,2
x5 = = 2314,8,
2
2531,2 + 2964,0
x6 = = 2747,6,
2
2964,0 + 3396,8
x7 = = 3180,4,
2
3396,8 + 3829,6
x8 = = 3613,2,
2
3829,6 + 4262,4
x9 = = 4046,0,
2
4262,4 + 4695,2
x10 = = 4478,8,
2
4695,2 + 5128,0
x11 = = 4911,6,
2
5128,0 + 5560,8
x12 = = 5344,4,
2
5560,8 + 5993,6
x13 = = 5777,2,
2
5993,6 + 6426,4
x14= = 6210,0,
2
6426,4 + 6859,2
x15 = = 6642,8;
2
- частоты (условие):
ai < xi < bi ;
- частости:
ni ni
Wi = = ,
n 69
11
W1 = = 0,16,
69
37
W2 = = 0,54,
69
13
W3 = = 0,19,
69
5
W4 = = 0,08,
69
1
W5,7,15 = = 0,01,
69
4. Рассчитаем первый и девятый децили и децильный коэффициент дифференциации среднедушевого дохода:
Первая дециль:
1 1
N Д1 = * n = * 69 = 6,9;
10 10
- по столбцу Cum F: Д 1 принадлежит 1-му интервалу, т.к. (6,9 < 11), т.е. интервалу (367,2 – 800,0)
1/10 * n - ∑f1
Д 1 = x н + h *
f2
xн = 367,3,
h = 432,8,
1/10 * n = 6,9,
∑f1 = 0,
f2 = 11,
6,9 - 0
Д 1 = 367,3 + 432,8 * = 638,8 (руб.),
11
т.е. максимальный среднедушевой доход для 10% самого бедного населения равен 638,8 рублей.
Девятая дециль:
9 9
N Д9 = * n = * 69 = 62,1;
10 10
- по столбцу Cum F: Д9 принадлежит 4-му интервалу, т.к. (61 < 62,1 < 66), т.е. интервалу (1665,7 – 2098,5)
1/10 * n - ∑f1
Д 9 = x н + h *
f2
x н = 1665,7,
h = 432,8,
9/10 * n = 62,1,
∑f1 = 61,
f2 = 5,
62,1 - 61
Д 9 = 1665,7 + 432,8 * = 1760,9 (руб.),
5
- это минимальный среднедушевой доход 10% самого богатого населения.
Децильный коэффициент дифференциации среднедушевого дохода:
Д 9 1760,9
КД = = = 2,8,
Д 1 638,8
т.е. минимальный среднедушевой доход самых богатых превышает макси-мальный среднедушевой доход самых бедных слоев населения в 2,8 раза.
Похожие работы
... которые устанавливаются нормативным методом с помощью научно разработанных нормативов потребления. При относительном подходе определяется минимальный потребительский бюджет (МПБ) статистическим методом исходя из фактически сложившегося потребления в домохозяйствах с низкими доходами. При субъективном подходе уровень низких доходов находится путем опроса общественного мнения. Измерение ПМ или ...
... потребления, но без учета «челночной» торговли, «оседающих» транзитных товаров и неэквивалентного бартера. Лекция 17 Статистика предпринимательства 1.Социально-экономическая сущность предпринимательства и задачи статистики. 2.Показатели статистики предпринимательства. Особенности статистического изучения малого предпринимательства 3.Тенденции развития малого предпринимательства в ...
... его в нашем примере возможен лишь в тех случаях, когда структура потребительских расходов населения за два сравниваемых периода претерпела принципиальные, качественные изменения, что делает невозможным использование в качестве весов ни текущую, ни базисную структуры расходов. В практике международной статистики цен индекс Фишера применяется при оценке динамики цен внешней торговли и в двусторонних ...
... налогооблагаемой базы , Совокупное изменение налоговых поступлений в бюджет Средняя процентная ставка по налогу рассчитывается по формуле , где i – процентная ставка по налогу; v – размер облагаемого совокупного дохода (налогооблагаемая база). СТАТИСТИКА УРОВНЯ ЖИЗНИ НАСЕЛЕНИЯ Индекс развития человеческого потенциала рассчитывается как средняя арифметическая из трех ...
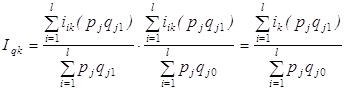
0 комментариев