Навигация
Характеристика часових рядів, структура та підходи до статистичного вивчення
2.1 Характеристика часових рядів, структура та підходи до статистичного вивчення
Сучасні дослідження макроекономічної динаміки, процесів перехідної економіки, фінансових ринків спираються на аналіз взаємозв’язків соціально-економічних даних, що має вигляд часових рядів. Урахування часової структури даних щодо реальних економічних процесів дозволяє адекватно відображати їх в економіко-математичних моделях. Усвідомлення цього факту зумовило як ревізію багатьох макроекономічних теорій, так і бурхливий розвиток специфічних методів аналізу таких даних. Знання цих методів і способів застосування їх до прогнозування соціально-економічних процесів є необхідною складовою підготовки економістів-дослідників (аналітиків).
Соціально-економічні процеси найчастіше спостерігаються у вигляді ряду послідовних, розташованих у хронологічному порядку значень того чи того показника.
Динамічний ряд — це сукупність спостережень одного показника, впорядкованих залежно від значень іншого показника, що послідовно зростають або спадають.
Часовий ряд (time series) — це ряд динаміки, впорядкований за часом, або сукупність спостережень економічної величини в різні моменти часу.
Теоретично вимірювання можна реєструвати безперервно, але зазвичай їх здійснюють через однакові проміжки часу, тобто дискретно, і нумерують за елементами вибірки. Складовими ряду спостережень є числові значення показника, які називають рівнями ряду, та моменти або інтервали часу, до яких належать рівні. Часовий ряд (ЧР) можна записати у стислому вигляді:
![]() ,
, ![]() ,
,
де ![]() — рівновіддалені моменти спостережень (година, доба, місяць, квартал, рік тощо)[2]. Під довжиною часового ряду розуміють час, що минув від першого до останнього моменту спостереження. Часто довжиною ряду називають кількість рівнів n, які утворюють часовий ряд.
— рівновіддалені моменти спостережень (година, доба, місяць, квартал, рік тощо)[2]. Під довжиною часового ряду розуміють час, що минув від першого до останнього моменту спостереження. Часто довжиною ряду називають кількість рівнів n, які утворюють часовий ряд.
Залежно від характеру досліджуваних соціально-економічних показників часові ряди поділяють на моментальні, інтервальні та похідні.
Часові ряди, утворені показниками, що характеризують економічне явище на певні моменти часу, називають моментальним.
Якщо рівні часового ряду утворюються шляхом агрегування за певний проміжок (інтервал) часу, такі ряди називають інтервальними часовими рядами.
Часові ряди можуть бути створені як із абсолютних значень економічних показників, так і з середніх або відносних величин — це похідні ряди.
Основні характеристики динаміки розвитку соціально-економічних процесів. Для аналізу соціально-економічних показників абсолютні рівні моментальних або інтервальних часових рядів, а також рівні середніх величин часто доводиться перетворювати на відносні величини. Найпоширеніші характеристики динаміки розвитку соціально-економічних процесів та їхні розрахунки наведено в табл. 2.1.
Таблиця 2.1ХАРАКТЕРИСТИКИ ДИНАМІКИ ЧАСОВОГО РЯДУ
| Характеристики | Розрахункові формули |
| 1. Абсолютний приріст |
|
| 2. Коефіцієнт зростання |
|
| 3. Коефіцієнт приросту |
|
| 4. Темп зростання |
|
| 5. Темп приросту |
|
| 6. Середня арифметична |
|
| 7.Середня хронологічна |
|
| 8. Середній абсолютний приріст |
|
| 9. Середній темп зростання |
|
| 10. Середній темп приросту |
|
Для визначення змін, що відбуваються з досліджуваним явищем, передусім обчислюють швидкість розвитку цього явища за часом. Показником швидкості слугує абсолютний приріст, який характеризує величину зміни показника за інтервал часу між порівнюваними періодами й обчислюється за формулою:
![]() , (2.1)
, (2.1)
де ![]() — і-й рівень часового ряду (
— і-й рівень часового ряду (![]() );
);
![]() — індекс початкового рівня;
— індекс початкового рівня; ![]() і може бути обраний будь-яким залежно від мети дослідження: за
і може бути обраний будь-яким залежно від мети дослідження: за ![]() отримують ланцюгові показники, за
отримують ланцюгові показники, за ![]() отримують базові показники із базовим початковим рівнем ряду тощо.
отримують базові показники із базовим початковим рівнем ряду тощо.
Точніше, швидкість зміни показника характеризує приріст за одиницю часу; ця величина має назву середнього абсолютного приросту:
![]() . (2.2)
. (2.2)
Зокрема, середній абсолютний приріст за весь період спостереження для заданого часового ряду дорівнює:
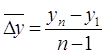 (2.3)
(2.3)
і характеризує середню швидкість зміни часового ряду, де ![]() — індекс останнього спостереження.
— індекс останнього спостереження.
Для визначення відносної швидкості зміни економічного явища як одиницю часу використовують відносні показники: коефіцієнти зростання й приросту (якщо ці показники виражені у відсотках, їх називають відповідно темпами зростання й приросту). Зазначимо, що в усіх наступних формулах індекс початкового рівня, стосовно якого здійснюють порівняння, також визначають за допомогою індексу k, як і раніше для показника абсолютного приросту.
Коефіцієнт зростання для і-го періоду обчислюють за формулою:
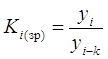 , (2.4)
, (2.4)
![]() , якщо рівень підвищується;
, якщо рівень підвищується; ![]() , якщо рівень зменшується; за
, якщо рівень зменшується; за ![]() рівень не змінюється.
рівень не змінюється.
Коефіцієнт приросту дорівнює:
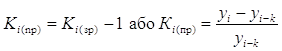 (2.5)
(2.5)
На практиці часто застосовують показники темпу зростання й темпу приросту:
![]() , (2.6)
, (2.6)
де ![]() — темп зростання для і-го періоду;
— темп зростання для і-го періоду;
![]() або
або ![]() , (2.7)
, (2.7)
де ![]() — темп приросту для і-го періоду. Темп приросту показує, на скільки відсотків рівень одного періоду збільшився стосовно рівня іншого періоду, тобто цей показник характеризує відносну величину приросту у відсотках.
— темп приросту для і-го періоду. Темп приросту показує, на скільки відсотків рівень одного періоду збільшився стосовно рівня іншого періоду, тобто цей показник характеризує відносну величину приросту у відсотках.
Порівняння абсолютного приросту та темпу приросту за той самий інтервал часу показує, що в реальних економічних процесах уповільнення темпу приросту часто не супроводжується зменшенням абсолютних приростів.
Абсолютне значення одного відсотка приросту визначають як відношення абсолютного приросту ![]() до темпу приросту у відсотках
до темпу приросту у відсотках ![]() .
.
Середню швидкість зміни показника, що вивчається, за певний період характеризує також середній темп зростання. Його розраховують за формулою середньої геометричної:
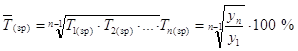 , (2.8)
, (2.8)
де ![]() — середні темпи зростання за окремі інтервали часу.
— середні темпи зростання за окремі інтервали часу.
Відповідно середній темп приросту визначають як:
![]() . (2.9)
. (2.9)
Показник середнього темпу зростання, обчислюваний за формулою середньої геометричної (2.8), має суттєві недоліки, оскільки ґрунтується на зіставленні останнього та початкового рівнів часового ряду, проміжні рівні до уваги не беруться. У разі суттєвого коливання рівнів використання середнього геометричного темпу зростання для статистичного аналізу може призвести до серйозних помилок, внаслідок чого реальна тенденція часового ряду буде викривлена.
Сучасні способи розрахунків середнього темпу зростання певною мірою позбавлені недоліків середньої геометричної. Наприклад, для розрахунків середнього темпу зростання пропонується використовувати формулу:
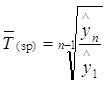 , (2.10)
, (2.10)
де ![]() ,
,![]() — згладжені за рівнянням тренду (рівнянням кривої зростання) перший та останній рівні часового ряду. У моделі тренду враховано коливання проміжних рівнів часового ряду, тому обчислені за нею значення
— згладжені за рівнянням тренду (рівнянням кривої зростання) перший та останній рівні часового ряду. У моделі тренду враховано коливання проміжних рівнів часового ряду, тому обчислені за нею значення ![]() та
та ![]() та середній темп зростання (2.10) точніше характеризуватимуть зміну економічного явища впродовж інтервалу дослідження.
та середній темп зростання (2.10) точніше характеризуватимуть зміну економічного явища впродовж інтервалу дослідження.
Якщо тенденція часового ряду не змінюється, використовують характеристику середнього рівня ряду. В інтервальному ряду динаміки з однаково розташованими в часі рівнями середній рівень ряду обчислюють за формулою простої середньої арифметичної (тут і далі додавання ведеться за всіма періодами спостережень):
![]() . (2.11)
. (2.11)
Якщо інтервальний ряд має неоднаково розташовані в часі рівні, тоді середній рівень ряду (так звану середню хронологічну) обчислюють за формулою зваженої арифметичної середньої, де вагою є тривалість часу (наприклад, кількість років), упродовж якого рівень постійний:
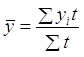 , (2.12)
, (2.12)
де t — кількість періодів часу, для яких значення рівня ![]() не змінюється.
не змінюється.
Для моментального ряду з однаково розташованими в часі рівнями середню хронологічну розраховують за формулою:
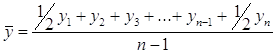 , (2.13)
, (2.13)
де п — кількість рівнів ряду.
Середню хронологічну для моментального часового ряду з неоднаково розташованими в часі рівнями розраховують за формулою:
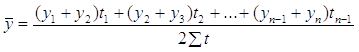 . (2.14)
. (2.14)
Тут п — кількість рівнів ряду, а t — період часу, що відокремлює 1-й рівень ряду від (t + 1)-го рівня.
Коригування рівнів часового ряду. Часовий ряд правильно відображає об’єктивний закон зміни економічного показника, коли рівні цього ряду є порівнянними, однорідними, сталими та мають достатню сукупність спостережень. Невиконання однієї із цих умов робить некоректним застосування математичного апарату для аналізу часового ряду.
Порівнянність означає, що рівні часових рядів повинні мати однакові одиниці вимірювання, однакову періодичність обліку окремих спостережень, однаковий ступінь агрегування, обчислюватися за тією самою методикою. В економіці й соціології найпоширенішими є такі причини непорівнянності:
· за територією, внаслідок зміни кордонів регіону, за яким збирають статистичні дані;
· за колом охоплення об’єктів і підпорядкуванням або формою власності. Наприклад, унаслідок переходу частини підприємств конкретного об’єднання до іншого;
· за часовим періодом, коли дані кількох років наведено за станом на різні дати, або місяці мають різну тривалість, на порівнянність економічних і соціологічних даних впливають свята;
· через розбіжність у структурі одиниць сукупності, для якої їх обчислено. Наприклад, дані стосовно кількості населення залежать не лише від зміни кількості народжених і померлих, а й від зміни вікового складу населення впродовж періоду спостереження;
· за вартісними показниками. Навіть у тих випадках, коли значення цих показників фіксуються в незмінних цінах, їх часто важко зіставити.
Існують й інші причини. Непорівнянність часових рядів неможливо усунути лише формальними методами, тому на неї зважають у процесі змістовного тлумачення рядів спостережень і результатів їхнього статистичного аналізу.
Однорідність означає відсутність нетипових, аномальних спостережень, а також викривлень тенденції. Під аномальним рівнем розуміють окреме значення рівня часового ряду, яке не відповідає потенційним можливостям економічної системи, що вивчається, і яке, залишаючись рівнем ряду, чинить суттєвий вплив на значення основних характеристик часового ряду. Формально аномальність виявляється як несподіваний стрибок (або спад) із подальшим поступовим встановленням попереднього рівня. Аномальність призводить до зміщення оцінок і, отже, до спотворення результатів аналізу. Причинами аномальних спостережень можуть бути помилки технічного порядку, або помилки першого роду: агрегування та дезагрегування показників, під час передання інформації та з інших технічних причин. Помилки першого роду слід виявляти й виправляти. Крім того, аномальні рівні в часових рядах можуть виникати через помилки другого роду: значення відображають об’єктивний розвиток процесу, але істотно відхиляються від загальної тенденції розвитку процесу; значення, що виникають через зміну методики обчислення, тощо. Ці помилки трапляються епізодично, тобто дуже рідко, і не підлягають усуненню. Для виявлення аномальних рівнів часових рядів використовують методи, призначені для статистичних сукупностей (метод Ірвіна тощо). Засоби описової статистики та обчислення їх за даними вибіркових спостережень наведено в дод.8
Метод Ірвіна ґрунтується на порівнянні сусідніх значень ряду та розрахунку характеристики ![]() , яка дорівнює:
, яка дорівнює:
![]() ; (2.15)
; (2.15)
де ![]() — оцінка середньоквадратичного відхилення вибіркового ряду
— оцінка середньоквадратичного відхилення вибіркового ряду ![]() , яка розраховується з використанням формул:
, яка розраховується з використанням формул:
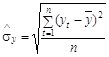 ,
, 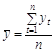 .
.
Розрахункові значення ![]() ,
, ![]() тощо порівнюють із критичним значенням
тощо порівнюють із критичним значенням ![]() , і якщо вони не перевищують критичне, то відповідні рівні
, і якщо вони не перевищують критичне, то відповідні рівні ![]() вважаються нормальними. Критичні значення для рівня значущості α = 0,05 (помилка 5 %) наведено в табл. 2.3
вважаються нормальними. Критичні значення для рівня значущості α = 0,05 (помилка 5 %) наведено в табл. 2.3
| п | 2 | 3 | 10 | 20 | 30 | 50 | 100 |
|
| 2,8 | 2,3 | 1,6 | 1,3 | 1,2 | 1,1 | 1,0 |
Критерій Ірвіна не «сприймає» аномальність, якщо вона виявляється в середині ряду зі стрімкою динамікою, тобто коли стрибок великий, але не перевищує рівнів наприкінці періоду спостережень, оскільки величина ![]() характеризує відхилення значень показника від середнього рівня за всією сукупністю спостережень.
характеризує відхилення значень показника від середнього рівня за всією сукупністю спостережень.
Модифікація цього методу пов’язана із послідовним розрахунком ![]() не за всією сукупністю, а за трьома спостереженнями. Так, для всіх або лише для підозрюваних в аномальності рівнів розраховують оцінки середнього і середньоквадратичного відхилення для двох сусідніх із ними значень:
не за всією сукупністю, а за трьома спостереженнями. Так, для всіх або лише для підозрюваних в аномальності рівнів розраховують оцінки середнього і середньоквадратичного відхилення для двох сусідніх із ними значень:
![]() (2.16)
(2.16)
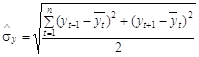 . (2.17)
. (2.17)
Обчислюють величину ![]() , t = 2, 3,…, n. (2.18)
, t = 2, 3,…, n. (2.18)
Розраховані ковзні значення ![]() порівнюють із критичними значеннями
порівнюють із критичними значеннями ![]() для
для ![]() .
.
Викривлення тенденції свідчить про зміну закономірності розвитку процесу або про зміну методики обчислення значень показника. Якщо точно встановлено, що причиною аномальності є помилки першого роду, то аномальні спостереження замінюють або простою середньою арифметичною двох сусідніх рівнів ряду, або відповідними значеннями за кривою, що згладжує цей часовий ряд. Не перевіряють часові ряди з періодом сезонності, більшим за одиницю, а також кінцеві рівні періоду спостережень.
Якщо значення наприкінці часового ряду «випадає» із загальної тенденції, то без додаткової інформації стосовно причин «випадіння» в кінці ряду неможливо визначити, чи це спостереження аномальне, чи відбувається зміна тенденції. У цьому разі важливо провести якісний аналіз змін, що відбуваються, або дочекатися надходження результатів нового спостереження. Якщо викривлення тенденції пояснюється зміною методики обчислення показника, то рівні, що передують викривленню тенденції, можуть бути використані для оцінювання характеристик динаміки і побудови моделі за умови, що вони будуть обчислені за новою методикою. Якщо таке обчислення неможливе, ці рівні ряду треба виключити з розгляду. Якщо викривлення тенденції відображає зміну закономірності розвитку процесу, то за інформаційну базу для статистичного аналізу можна взяти лише значення, що відповідають останнім змінам.
Стійкість часового ряду відбиває перевагу закономірності над випадковістю у зміні рівнів ряду. На графіках стійких часових рядів унаочнюється закономірність, а на графіках несталих рядів зміни послідовних рівнів постають хаотичними, тож пошук закономірностей формування значень рівнів таких рядів марний.
Достатня сукупність спостережень насамперед характеризує повноту даних. Достатня кількість спостережень визначається залежно від мети дослідження динаміки. Якщо метою є описовий статистичний аналіз, то період дослідження можна обрати будь-який, на власний розсуд. Якщо мета дослідження — побудова прогнозної моделі, тоді для статистичного аналізу, який розглядає незалежні спостереження з однаковим розподілом, кількість рівнів динамічного ряду має бути якомога більшою і, як правило, не менш як утричі має перевищувати період упередження прогнозу й становити більше 7. У разі використання квартальних або місячних даних для дослідження сезонності й прогнозування сезонних процесів часовий ряд має містити квартальні або місячні дані не менш як за чотири роки, навіть якщо складають прогноз на 1—2 квартали (місяці).
У методах нелінійної динаміки підхід до формування достатньої кількості даних відрізняється від прийнятого більшістю статистиків. У стандартній статистичній теорії чим більше даних точок спостережень, тим краще, бо спостереження передбачаються як незалежні. Нелінійні динамічні системи характеризуються процесами із довготривалою пам’яттю. Тому для них охоплення більшого періоду часу є важливішим, ніж збільшення кількості точок спостережень. Наприклад, щоденна вибірка за чотири роки, або 1040 спостережень, не дадуть такого результату, як щомісячні дані за сорок років, або загалом 480 спостережень. Причина полягає в тому, що щоденні дані утворюють лише один чотирирічний цикл, а щомісячні — десять циклів. Нелінійні процеси мають так звану «стрілу часу». Збільшення «частоти» даних часто навіть ускладнює аналіз і не поліпшує значущості результату.
Серед чинників, що визначають регулярні коливання ряду, розрізняють такі:
Сезонні, що відповідають коливанням, які мають періодичний або близький до нього характер упродовж одного року. Наприклад, ціни на сільгосппродукцію взимку вищі, ніж улітку ; рівень безробіття в курортних містах у зимовий період зростає відносно до літнього. Сезонні чинники можуть охоплювати причини, пов’язані з діяльністю людини (свята, відпустки, релігійні традиції тощо). Результат дії сезонних чинників моделюють за допомогою функції ![]() .
.
Циклічні (кон’юнктурні) коливання схожі на сезонні, але виявляються на триваліших інтервалах часу. Циклічні коливання пояснюються дією довготермінових циклів економічної, демографічної або астрофізичної природи. Наприклад, за багаторічними спостереженнями активність сонця має циклічність у 10,5—11 років, причому сплески сонячної радіації впливають на врожайність зернових культур, репродуктивну властивість тварин тощо. Отже динаміка показника міситиме характерні зміни, що повторюються з однаковою циклічністю. Результат дії циклічних чинників моделюють за допомогою функції ![]() .
.
Тренд, сезонна й циклічна компоненти не є випадковими, тому їх називають систематичними компонентами часового ряду.
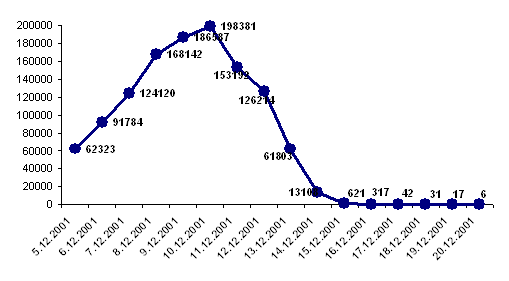
Випадкові чинники не підлягають вимірюванню, але неминуче супроводжують будь-який економічний процес і визначають стохастичний характер його елементів. До випадкових чинників можна віднести помилки вимірювання, випадкові збурення тощо. Деякі часові ряди, наприклад стаціонарні, не мають тенденції та сезонної складової, кожен наступний рівень їх утворюється як сума середнього рівня ряду і випадкової (додатної або від’ємної) компоненти. Приклад такого ряду демонструє рис. 2.1 в.
Результат впливу випадкових чинників позначається випадковою компонентою εt, яку обчислюють як залишок або похибку, що залишається після вилучення з часового ряду систематичних компонент. Це не означає, що така складова не підлягає подальшому аналізу, оскільки містить лише хаос.
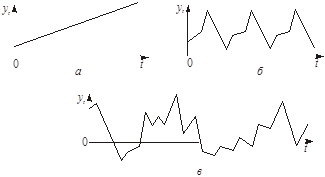
Рис. 2.1. Головні компоненти часового ряду: а — тренд, що зростає; б — сезонна компонента; в — випадкова компонента
Похожие работы
... Рівненській області протягом останнього десятиріччя носить хвилеподібний характер. Перша хвиля припадає на 19911995 роки, по Україні відбувається зростання з 12,9 до 15,4 померлих на 1000 населення, а по Рівненській області відповідно з 13,3 до 15,3. В 19961998 рр. відбувається зниження смертності: по Україні до 14,3 і на Рівненщині до 14,7, а згодом в 19992003 рр. Знову підвищення (друга “хвиля ...
... непрацездатності тощо), здійснюється за даними довідок-розрахунків та інших додаткових документів (наказів директора підприємства, лікарняних листків тощо). [2]. 3. Статистичне використання робочої сили і робочого часу в Україні 3.1 Робоча сила Загальна чисельність економічно активного населення залишається практично незмінною від початку виходу з кризи і становить 22,6 млн. осіб. Однак ...
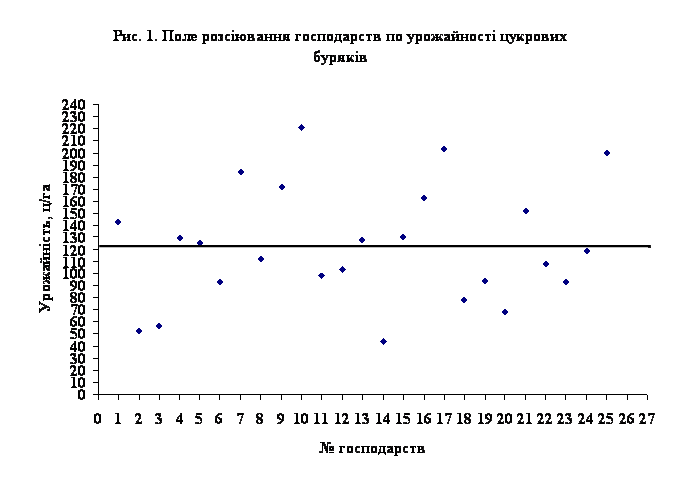
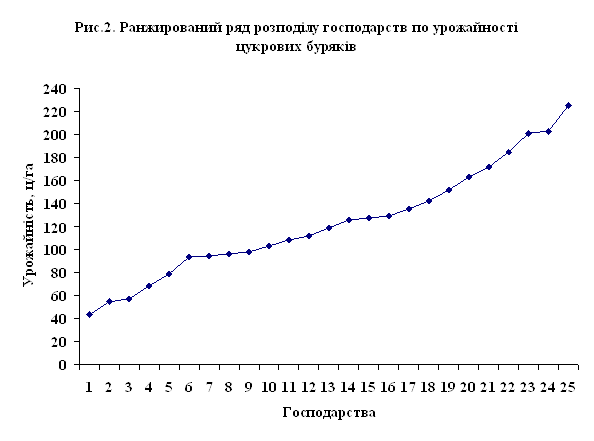
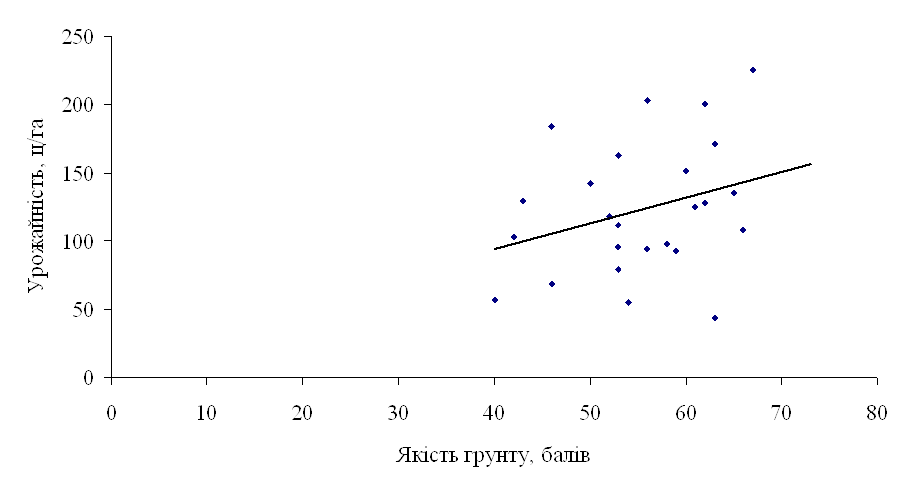
... лінію регресії (рис.4). Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту Розділ IV. Динаміка та прогнозування урожайності цукрових буряків 4.1 Перспективи розвитку урожайності цукрових буряків в господарствах Андрушівського району Рядом динаміки називається тимчасова послідовність значень статистичних показників. Ряд динаміки складається із ...
... або 10%, 172 тис. шт. або 72%, також збільшився товарообіг машин МПДН-1А та вагонів рудничних ВГ-2,1-750.000.00 на 134 тис. шт. або 34% та 134 тис. шт. 69%. 2.4 Розрахунок питомої ваги товарообігу промислової продукції підприємстві РМЗ Обчислимо відносні величини структури (питому вагу) товарообігу промислової продукції на підприємстві РМЦ. Питома вага – це співвідношення розмірів частин і ...
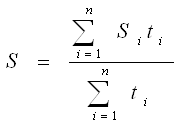
0 комментариев