Поняття ціни, її види та функції
Система статистичних показників цін та методика їх побудови
Організація статистичних спостережень за цінами
Формування бази зважування і визначення формули розрахунку
Характеристика часових рядів, структура та підходи до статистичного вивчення
Метод сезонної декомпозиції як основа статистичного вивчення часових рядів
Вилученням сезонної компоненти із початкового часового ряду одержують десезоналізований ряд
Статистичний аналіз цін виробників промислової продукції у Львівській області
Транскордонні порівняння динаміки цін виробників промислової продукції Львівщини та Польщі (Підкарпатського воєводства)
Навигация
Вилученням сезонної компоненти із початкового часового ряду одержують десезоналізований ряд
Статистичне вивчення та прогнозування динаміки цін на промислову продукцію
134760
знаков
25
таблиц
33
изображения
4. Вилученням сезонної компоненти із початкового часового ряду одержують десезоналізований ряд.
5. Аналітичне згладжування десезоналізованого ряду й отримання оцінок тренду 
.
6. Розрахунок невипадкової складової для адитивної моделі 
або мультиплікативної моделі 
.
7. Обчислення абсолютних або відносних похибок 
та перевірка адекватності моделі.
8. Розрахунок прогнозів.
Для розрахунку параметрів трендових моделей використано стандартні комп’ютерні програми.
Систематична складова (тренд) Ut характеризує основні довгострокові зміни часового ряду. Вибір тренду здійснюється, перш за все, на основі якісного економічного аналізу досліджуваного процесу. Також при виборі форми тренду попередній висновок щодо виду функції можна зробити, вивчаючи графік динамічного ряду. Окрім того, вважається, що більшість економічних процесів мають лінійну або близьку до неї тенденцію розвитку.
Таким чином, при побудові моделей часових рядів, які характеризують тенденції використано лінійну функцію:
Ut = a0 +a1 t.
Оцінку параметрів цих моделей здійснювали методом найменших квадратів, який є найбільш розповсюдженим, досить простим при обчисленнях і має досить якісні властивості оцінок.
Сезонній циклічності притаманне постійне повторюване коливання попиту та пропозиції протягом року. При оцінці сезонних коливань найчастіше розраховують індекс сезонності. Але індекси сезонності не виключають цілком вплив випадкових і другорядних факторів, тому доцільно використати методи вирівнювання динамічного ряду, зокрема метод ковзкої середньої, аналітичне вирівнювання, гармонійний аналіз або рівняння тренду з метою виявлення закономірностей сезонності, тенденцій сезонної хвилі.
Оскільки сезонна складова описує циклічні зміни, які повторюються з часом, то для цього як функцію можна використати ряд Фур’є, тобто проводити гармонійний аналіз відхилень емпіричних значень ряду від тренду.
Схематично використання гармонійного аналізу можна представити так. Спочатку з ряду виключають тренд. Після того, як з емпіричного ряду виключено столітню тенденцію, потрібно дослідити наявність циклічності. Гармонійний аналіз базується на теоремі Фур’є, суть якої полягає в тому, що будь-яку періодичну функцію, яку довільно задано в певному інтервалі, можна розкласти на ряд простих гармонійних коливань. Дану функцію можна відобразити тригонометричним рядом, який названо рядом Фур’є. Цей ряд Фур’є має вигляд [10, 15-17]:
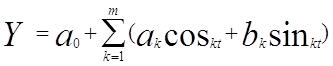
Тут t – номер гармоніки Фур’є; 0 a , k a , k b – параметри, які визначаються методом найменших квадратів; k – кількість гармонік,
K=2p / T = , де T – період коливання.
Використання методів дисперсійного аналізу свідчить, що найкращу апроксимацію можна досягти за умови включення в модель перших чотирьох гармонік.
Розрахункові значення часового ряду визначалися як сума значень систематичної складової (тренду) та випадкових складових (сезонності та випадковості)..
Точність одержаних прогнозів оцінювалась за величиною відносної похибки екстраполяції та її середнього значення
На основі одержаних моделей можна також передбачити, врахувати та зменшити наслідки прояву сезонності, зокрема такі як значні збитки, пов’язані з нерівномірністю використання обладнання, устаткування, робочої сили, сировини; з нерівномірним використанням інфраструктури, а також викликаною необхідністю створення різного роду резервів тощо. Тобто є можливість позбутися фактора невизначеності під час проведення кон’юнктурних досліджень у ході оцінювання та прогнозування майбутніх тенденцій і закономірностей, що має надзвичайно важливе практичне значення.
В теоретичному аспекті як результат даного дослідження можна взяти за основу запропоновану методику моделювання процесів на основі аналізу сезонних коливань.
2.3.Метод Хольта-Вінтерса як основа статистичного прогнозування індексів цін
Адаптивне прогнозування дає змогу автоматично змінювати константу згладжування в процесі обчислення. Інструментом прогнозування в адаптивних методах є математична модель з одним чинником «час».
Адаптивні моделі прогнозування — це моделі дисконтування даних, які здатні швидко пристосовувати свою структуру й параметри до зміни умов. Найважливіша особливість їх полягає у тому, що це саморегулювальні моделі, й у разі появи нових даних прогнози оновлюються із мінімальною затримкою без повторення спочатку всього обсягу обчислень.
Нехай ми перебуваємо в якомусь поточному стані, для якого відомий поточний рівень ряду 
й очікуване значення 
. Залежно від закладеної у модель гіпотези формування сподіваних значень розрізняють моделі адаптивних сподівань, неповного коригування, раціональних сподівань. Методи розрахунку доволі складні, тож розглянемо лише підхід до цієї проблеми. Схему такого процесу представлено на рис. 2.2.
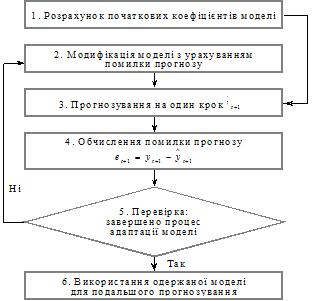
Після надходження фактичного значення обчислюється помилка, розбіжність між фактичним і прогнозованим рівнем (довготермінова функція моделі): 
.
У моделі передбачається, що зміна фактичного рівня є деякою часткою (
) від очікуваної зміни 
. Параметр 
називається коригувальним коефіцієнтом або параметром адаптації. За критерій оптимальності під час вибору параметра адаптації можна взяти мінімум середнього квадрата помилок прогнозування. Чим ближчий до одиниці, тим більше сподівання економічних суб’єктів відповідають реальній динаміці часового ряду, і навпаки, чим ближче до нуля — тим менше володіємо ситуацією, тому треба вносити корективи.
Помилка прогнозу через зворотний зв’язок надходить до моделі та враховується залежно від прийнятої системи переходу від одного стану до наступного. В результаті з’являються «компенсаційні» зміни, які дають змогу коригувати параметри моделі з метою більшого узгодження поведінки моделі з динамікою ряду. Наприклад, бажане значення 
якогось економічного показника визначається рівнянням:
(2.21)
де залишки 
є «білим шумом» і не корелюють із t. Фактичне значення на момент t ytне співпадає із бажаним значенням, але буде пристосовуватися до нього за таким правилом:
(2.22)
де 
— білий шум. Із (2.2.4) випливає, що на кожному кроці t рівень ряду yt,буде коригуватися в напрямі очікуваного значення 
на величину, пропорційну різниці між бажаним і поточним рівнями економічного показника. Співвідношення (2.2.4) можна переписати у вигляді експоненціальної середньої першого порядку:
(2.3)
з чого видно, що поточне значення величини yt є зваженим середнім бажаного рівня на даний момент часу та фактичного значення в попередньому періоді. Підставляючи значення (2.21) в (2.23), маємо модель коригування прогнозу:
(2.24)
Це співвідношення називають короткотерміновою функцією моделі.
Таким чином, адаптація здійснюється ітеративно з одержанням кожної нової фактичної точки ряду. Модель постійно «всмоктує» інформацію й розвивається з урахуванням нових тенденцій, наявних на теперішній момент. Завдяки зазначеним властивостям адаптивні методи найуспішніше використовують для оперативного прогнозування.
У практиці статистичного прогнозування базовими адаптивними моделями вважаються моделі Брауна і Хольта, які належать до схеми ковзної середньої, та модель авторегресії. Решта адаптивних методів (метод адаптивної фільтрації (МАФ), метод гармонійних ваг тощо [27]) розрізняються за способом оцінювання параметрів моделі та визначенням параметрів адаптації базових моделей.
Адаптивна модель за методом Хольта — це динамічний процес у вигляді лінійно-адитивного тренду:
(2.25)
де 
— прогнозована оцінка рівня ряду 
, яка розраховується в момент часу 
на 
кроків уперед,
— оцінка поточного (
-го) рівня часового ряду,
— оцінка поточного приросту.
Припускається, що випадкові залишки е мають нормальний закон розподілу із нульовим математичним сподіванням та дисперсією 
.
У цьому методі послаблені умови однопараметричності моделі Брауна за рахунок уведення двох параметрів згладжування — 
та 
, (
).
Коефіцієнти лінійної моделі за методом Хольта розраховують за такими співвідношеннями:
, (2.26 )
, (2.27 )
де еt — похибка прогнозу рівня , обчислена в момент часу (t-1) на один крок уперед, 
.
Коефіцієнт 
має значення, близьке до останнього рівня, і становить закономірну складову цього рівня; коефіцієнт
— визначає приріст, що склався наприкінці періоду спостережень, але характеризує також швидкість зростання показника попередніх етапах. Початкові значення параметрів моделі знаходять за методом найменших квадратів на підставі кількох перших спостережень. Оптимальні значення параметрів згладжування та визначають методом багатовимірної числової оптимізації, вони є сталими для всього періоду спостереження.
Після оцінювання параметрів та прогноз на τ моментів часу, тобто , розраховують як суму оцінки середнього поточного значення (
) та очікуваного показника зростання (
), помноженого на період випередження τ, тобто
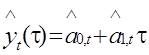. (2.28 )
За допомогою оператора L можна зрушити всю послідовність даних на один крок назад: 
. Застосування оператора 
до спостережень і коефіцієнтів моделі Хольта дає змогу представити її як модель ARIMA (0, 1, 1) у вигляді:
. (2.29 )
Формулювання адаптивних моделей у термінах лінійних параметричних моделей ARMA (авторегресії — ковзної середньої) — уможливлює також тлумачення їх як підмножини класу лінійних параметричних моделей. Отже, встановлюється відповідність між двома різними підходами до моделювання часових рядів.
Метод Хольта-Вінтерса. Цей метод, на відміну від мето-
ду Хольта, окрім лінійного тренду включає ще й сезонну компоненту.
Прогноз на τ кроків уперед для адитивної форми моделі будують за формулою:
, (2.30 )
де s — коефіцієнт сезонності;
m — період сезонного циклу (наприклад, за квартальними даними m = 4). Обчислення параметрів моделі виконують за співвідношеннями:
, (2.31 )
, (2.32 )
, (2.33)
де 
— параметри згладжування (адаптації), 
.
Мультиплікативна модель аналогічна адитивній моделі з тією лише різницею, що розраховані за лінійною моделлю прогнозові значення коригують шляхом множення їх на сезонні коефіцієнти. Прогноз на τ кроків розраховують за формулою:
, (2.34)
а параметри обчислюють за співвідношеннями:
, (2.35)
, (2.36)
. (2.37)
Для несезонних часових рядів обчислювальні формули спрощують за рахунок виключення сезонної компоненти. За відносно постійної амплітуди сезонної хвилі доцільно використовувати адитивну модель, у разі її зміни відповідно до тенденції середнього рівня — мультиплікативну. Зазначимо, що моделі змішаного типу іноді дають точніший результат, але погано тлумачаться змістовно. Практика показує, що у випадку, коли сезонні коливання процесу великі й не дуже стабільні, мультиплікативна модель дає неточні результати.
У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1].
РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ
Похожие работы
... Рівненській області протягом останнього десятиріччя носить хвилеподібний характер. Перша хвиля припадає на 19911995 роки, по Україні відбувається зростання з 12,9 до 15,4 померлих на 1000 населення, а по Рівненській області відповідно з 13,3 до 15,3. В 19961998 рр. відбувається зниження смертності: по Україні до 14,3 і на Рівненщині до 14,7, а згодом в 19992003 рр. Знову підвищення (друга “хвиля ...
... непрацездатності тощо), здійснюється за даними довідок-розрахунків та інших додаткових документів (наказів директора підприємства, лікарняних листків тощо). [2]. 3. Статистичне використання робочої сили і робочого часу в Україні 3.1 Робоча сила Загальна чисельність економічно активного населення залишається практично незмінною від початку виходу з кризи і становить 22,6 млн. осіб. Однак ...
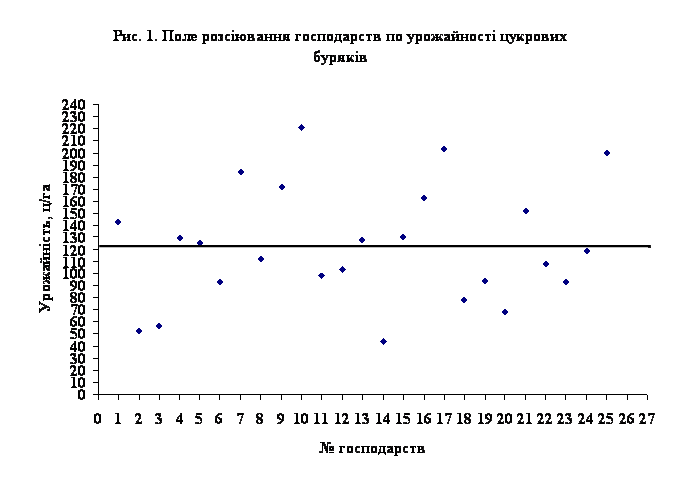
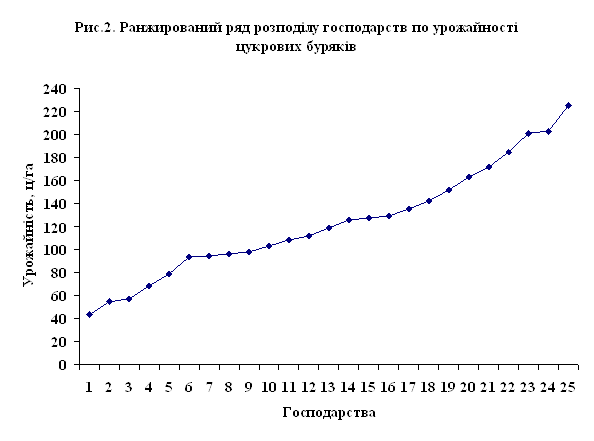
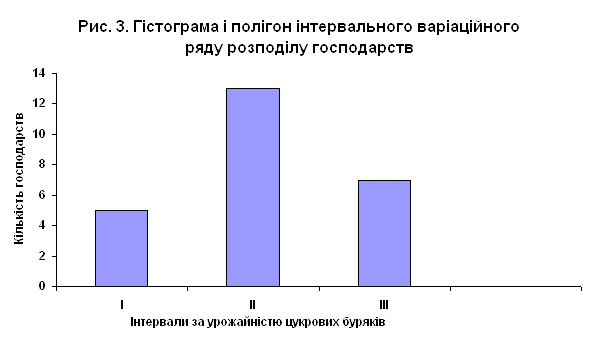
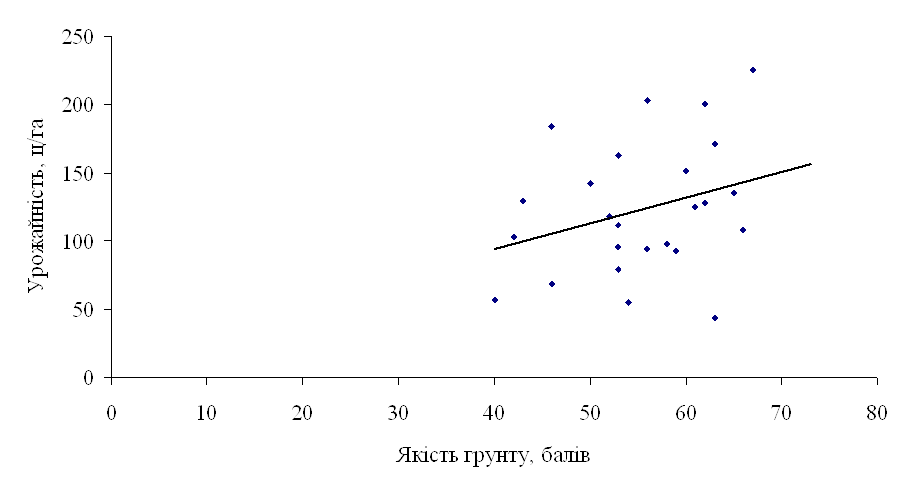
... лінію регресії (рис.4). Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту Розділ IV. Динаміка та прогнозування урожайності цукрових буряків 4.1 Перспективи розвитку урожайності цукрових буряків в господарствах Андрушівського району Рядом динаміки називається тимчасова послідовність значень статистичних показників. Ряд динаміки складається із ...
... або 10%, 172 тис. шт. або 72%, також збільшився товарообіг машин МПДН-1А та вагонів рудничних ВГ-2,1-750.000.00 на 134 тис. шт. або 34% та 134 тис. шт. 69%. 2.4 Розрахунок питомої ваги товарообігу промислової продукції підприємстві РМЗ Обчислимо відносні величини структури (питому вагу) товарообігу промислової продукції на підприємстві РМЦ. Питома вага – це співвідношення розмірів частин і ...
0 комментариев