Навигация
Многофакторный корреляционно-регрессионный анализ инвестиций
3.3. Многофакторный корреляционно-регрессионный анализ инвестиций.
Для корреляционно-регрессионного анализа необходимо из нескольких факторов произвести предварительный отбор факторов для регрессионной модели. Сделаем это по итогам расчета коэффициента корреляции. А именно возьмем те факторы, связь которых с результативным признаком будет выражена в большей степени. Начнем наш анализ с рассмотрения следующих факторов:
- Обменный курс рубля (поквартально, среднее значение за квартал) - x1 (руб./дол.)
- Доход на душу населения (поквартально, общее значение за квартал) – x2 (руб./квартал)
- Промышленное производство (поквартально, общее значение за квартал) – x3 (млрд. руб./квартал)
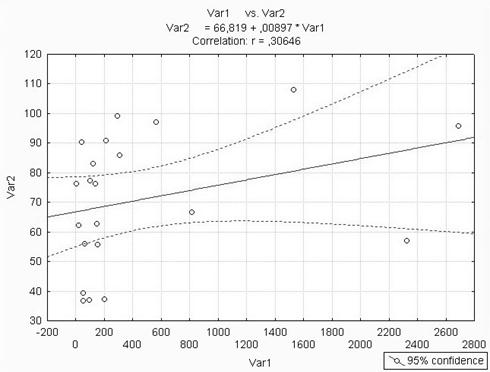
Рассчитаем коэффициент корреляции для линейной связи и для имеющихся факторов - x1, x2 и x3. Коэффициент корреляции определяется по следующей формуле:

где: ![]() и
и ![]() – дисперсии факторного и результативного признака
– дисперсии факторного и результативного признака
соответственно;
xy – среднее значение суммы произведений значений факторного и
результативного признака;
x и y – средние значения факторного и результативного признака
соответственно.
Данные, необходимые для расчётов представлены в приложении G.
Для фактора x1 после подстановки данных в формулу, получаем следующий коэффициент корреляции r1:
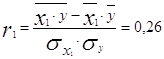
Для фактора x2 после подстановки данных в формулу, получаем следующий коэффициент корреляции r2:

Для фактора x3 после подстановки данных в формулу, получаем следующий коэффициент корреляции r3:
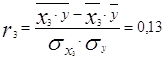
По полученным данным можно сделать вывод о том, что:
1) Связь между x1 и y прямая (так как коэффициент корреляции положительный) и слабая, так как она находится между 0,21 и 0,30. Тем не менее, будем использовать фактор в дальнейших расчётах.
2) Связь между x2 и y прямая (так как коэффициент корреляции положительный) и умеренная, так как она находится между 0,31 и 0,40. Данный фактор также будем использовать в дальнейших расчётах.
3) Связь между x3 и y отсутствует, так как коэффициент корреляции меньше 0,15. Таким образом, возникает необходимость исключить данный фактор из дальнейших исследований.
В целом мы выполнили поставленную задачу, определив два наиболее влиятельных фактора для дальнейших исследований. Это: обменный курс рубля (слабая связь) и доход на душу населения (умеренная связь).
Далее для данных факторов x1 и x2 рассчитываем показатели вариации для анализа исходных данных:
- размах колебаний - R;
- среднее линейное отклонение - d;
- дисперсию - ![]() ;
;
- среднее квадратичное отклонение - ![]() ;
;
- коэффициент вариации - V.
Данные показатели рассчитываются по следующим формулам:
![]()
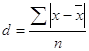
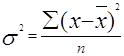
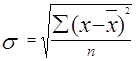
![]()
где:
хмах и хmin - соответственно максимальное и минимальное значения
фактора.
Рассчитаем данные показатели для факторов x1 и x2 . Данные для расчётов можно взять из приложения G. Для x1 :
R = 28,534 - 6,048 = 22,486 ;
d = 88,14/12 = 7,345;
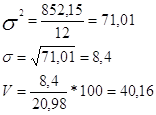
Коэффициент вариации V > 15%. Из этого можно сделать вывод, что совокупность нельзя признать однородной. Данная модель не может применяться на практике, однако в учебных целях продолжим наш анализ, используя данный фактор.
Для x2 :
R = 7748,7-2500,9 = 5247,8 ;
d = 16740,5/12=1395,04;
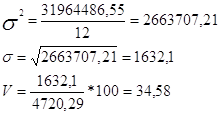
Полученный коэффициент вариации V также больше 15%, поэтому можно сделать вывод о том, что совокупность нельзя признать однородной, а следовательно использовать модель на практике. Однако в учебных целях продолжим рассмотрение влияния данного факторного признака на наш результативный признак.
Для фактора x1 (обменный курс рубля (поквартально, среднее значение за квартал), руб./дол.) проанализируем две следующие формы связи:
- Линейную (прямая форма связи);
- Параболическую;
Уравнение прямой имеет следующий вид: ŷ = a + bx1
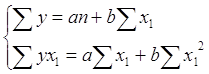 |
Для вывода данного уравнения необходимо решить следующую систему уравнений:
Уравнение параболы имеет следующий вид: ŷ = a + bx1 + cx12
Для вывода данного уравнения необходимо решить следующую систему уравнений:
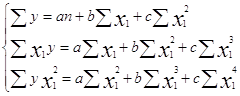
Все необходимые расчеты параметров А и B для линейной модели представлены в приложении I, а для А, В и С для параболы представлены также в приложении I.
После расчетов получаем два параметризованных уравнения:
Прямая – ŷ = 540,301 + 7,476*x1;
Парабола – ŷ = -111,026 +113,276*x1 – 3,068*(x1)2
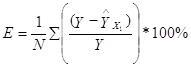 |
По нижеприведённой формуле рассчитаем ошибки аппроксимации для уравнений прямой и параболы (данные в приложении J). У какого уравнения будет наименьшая ошибка, то и оставляем для дальнейшего исследования:
Рассчитаем ошибку аппроксимации для прямой:
![]()
Рассчитаем ошибку аппроксимации для параболы:
![]()
Так как минимальная ошибка аппроксимации в уравнении параболы (7,35%), то данное уравнение мы оставляем для дальнейшего анализа. Однако эта ошибка больше 5%, то есть данную модель нельзя использовать на практике, но в учебных целях продолжим наш анализ, используя уравнение параболы.
Для уравнения проведем оценку параметров на типичность по формулам:
Данные для расчёта - в приложении G и J.
 | 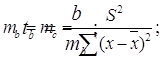 | 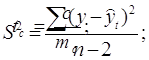 | |||
где: S2 – остаточная уточненная дисперсия;
S – среднее квадратическое отклонение от тренда;
ŷt – расчетные значения результативного признака;
ma, mb, mc – ошибки параметров;
ta, tb, tc – расчетные значения t критерия Стьюдента.
Рассчитаем значения данных величин:
S2 = 486117,16/10 = 48611,716;
![]()

mb = mc= 48611,716/852,15 = 57,046;
tb = 113,276/57,046= 1,986;
tc = 3,068/57,046 = 0,054;
Сравним полученные значения для α = 0,05 и числа степеней свободы
V = 10 (12 – 2) с теоретическим значением t-критерия Стьюдента. Для
α = 0,05 и числа степеней свободы V = 10 значение tтеор = 2,228. Расчетные значения ta , tb и tc < tтеор. Это значит, что данный параметр не типичен, что еще раз говорит нам о том, что данную модель нельзя использовать на практике. Однако в учебных целях продолжим наше исследование.
Для фактора x2 (доход на душу населения (поквартально, общее значение за квартал) (руб./квартал)) рассмотрим две формы связи:
- Линейную (прямую форму связи);
- Гиперболическую;
Уравнение прямой будет иметь вид: ŷ = a + bx2
 |
Для вывода данного уравнения необходимо решить следующую систему уравнений:
Уравнение гиперболы имеет следующий вид вид: ŷ = a + b(1/x2)
Для вывода данного уравнения необходимо решить следующую систему уравнений:
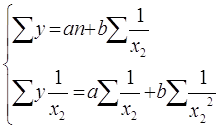
Все необходимые данные для расчётов представлены в приложении К.
После решения систем уравнений получается два параметризованных уравнения:
- ŷ = 472,3682 + 0,0476x2 - уравнение прямой;
- ŷ = 916,844 – 909008,4(1/x2) - уравнение гиперболы.
Рассчитаем ошибки аппроксимации для уравнений прямой и гиперболы. У какой модели она будет наименьшая, ту модель используем для дальнейшего исследования. Данные для расчёта ошибки аппроксимации находятся в приложении L.
Рассчитаем ошибку аппроксимации для прямой:
![]()
Для гиперболы рассчитаем ошибку аппроксимации:
![]()
Так как минимальная ошибка аппроксимации в уравнении гиперболы (9,19%), то данное уравнение мы оставляем для дальнейшего анализа. Однако эта ошибка больше 5%, то есть данную модель нельзя использовать на практике, но в учебных целях продолжим наш анализ, используя уравнение гиперболы.
Для уравнения проведем оценку параметров на типичность по формулам:
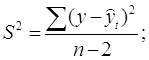 | 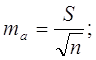 |
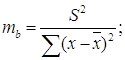 | 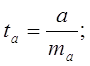 | 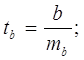 | |||
где: S2 – остаточная уточненная дисперсия;
S – среднеквадратическое отклонение от тренда;
ŷt – расчетные значения результативного признака;
ma, mb – ошибки параметров;
ta, tb – расчетные значения t критерия Стьюдента.
Подставим данные в формулы (приложение G и L) и рассчитаем значения данных величин:
S2 = 631712,98/10 = 63171,298;
![]()
![]()
ta = 916,844/72,555 = 12,64;
mb = 63171,298/2663707,21 = 0,0237;
tb = 909008,4/0,0237 = 38329626,04;
Полученные значения сравним с теоретическим значением t-критерия Стьюдента при α = 0,05 и V = 10 (12 – 2) составляет 2,228. Как видно из сопоставления ta и tb > tтеор, следовательно параметры типичны и существенны. По ним можно проводить дальнейший анализ.
Оценку существенности связи произведу на основе t-критерия Стьюдента. Он рассчитывается по следующей формуле:
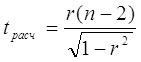
где:
r – коэффициент корреляции;
n – число уровней ряда;
После подстановки данных в формулу и произведённого расчёта получаем следующий показатель:
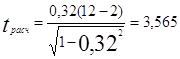
Так как tрасчётное > t теоретическое , или 3,565 > 2,228 при уровне значимости
α = 0,05 и числе степеней свободы V = 10 (12 – 2), связь x2 c y можно признать существенной и данный фактор можно использовать в дальнейшем анализе.
Для имеющихся факторов x1 и x2 составим уравнение множественной регрессии. Уравнение множественной регрессии изучает статистические закономерности между результативным признаком и несколькими факторами, влияющими на результат.
Для анализа уравнения множественной регрессии воспользуемся линейной формой связи. Составим линейное уравнение. На это есть следующие причины:
- Линейное уравнение легче подвергать анализу, интерпретации;
- В многочленах различных степеней каждый член степени, находящейся выше первой, может рассматриваться как новая переменная и таким образом уравнение переводится в линейную форму.
На основе имеющихся данных будем подвергать анализу во множественной регрессии следующие факторы:
- обменный курс рубля (поквартально, среднее значение за квартал) - x1 (руб./дол.)
- доход на душу населения (поквартально, общее значение за квартал) – x2 (руб./квартал)
Данные факторы проверим на мультиколлинеарность, для чего рассчитаем коэффициент корреляции rx1x2 ,то есть между факторами x1и x2. Он рассчитывается по формуле:

где: ![]() и
и ![]() – дисперсии факторного и результативного признака соответственно;
– дисперсии факторного и результативного признака соответственно;
x,y – среднее значение суммы произведений значений факторного и
результативного признака;
x и y – средние значения факторного и результативного признака
соответственно. Подставив имеющиеся данные (Приложение G и М) в формулу имеем следующее значение:
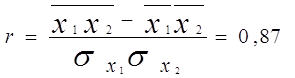
Полученный коэффициент говорит об очень высокой связи, то есть влияние одного фактора во множественной регрессии осуществляется через другой фактор, поэтому дальнейший анализ по обоим факторам вестись не может. Однако в учебных целях продолжим анализ.
Дольше проведу оценку существенности связи с помощью коэффициента множественной корреляции. Он показывает совокупное влияние факторов, включенных в модель и находится по следующей формуле по формуле:
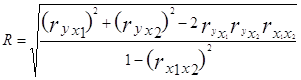
где: ryx1 – коэффициент корреляции между y и x1;
ryx2 – коэффициент корреляции между y и x2;
rx1x2 – коэффициент корреляции между x1 и x2.
Подставив имеющиеся данные в формулу, получил следующую цифру:
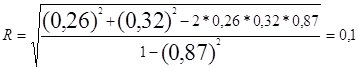
Так как величина множественного коэффициента корреляции R < 0,8, то связь признаем не существенной, но, тем не менее, в учебных целях, провожу дальнейшее исследование.
Уравнение прямой имеет следующий вид: ŷ = a + bx2 + cx3
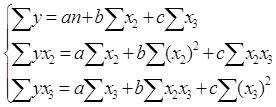 |
Для определения параметров уравнения необходимо решить систему:
Все необходимые данные, для расчёта данной системы уравнений представлены в приложениях М, К, L, J, I.
После произведённых расчётов имеем следующее уравнение прямой:
ŷ = -12,026 + 65,2763x2 – 0,186x3
Для данного уравнения найдем ошибку аппроксимации (все необходимые расчеты представлены в приложении N).
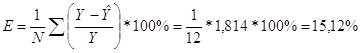
Так как ошибка аппроксимации E > 5%, то данную модель нельзя использовать на практике, но в учебных целях продолжим наш анализ.
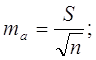 |  | 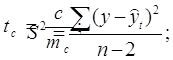 |
Проведем оценку параметров на типичность по формулам:
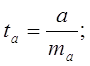 | 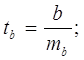 | ||
где: S2 – остаточная уточненная дисперсия;
S – среднеквадратическое отклонение от тренда;
ŷt – расчетные значения результативного признака;
ma, mb, mc – ошибки параметров;
ta, tb, tc – расчетные значения t критерия Стьюдента.
Рассчитаем значения данных величин:
S2 = 2003603/10 = 200360,3;
![]() ;
;
![]() ;
;
ta = -12,026/129,216 =-0,093;
mb = 200360,3/31964486,55 = 0,0063;
mc = 200360,3/852,15 = 235,1233;
tb = 65,276/0,0063 = 10361,269;
tc = -0,186/235,1233 = -0,0008.
Сравним полученные выше значения для α = 0,05 и числа степеней свободы V = 10 (12 – 2) с теоретическим значением t-критерия Стьюдента, который равен = 2,228, то есть tтеор = 2,228. Расчетные значения ta (-0,093) и tс (-0,0008) < tтеор, значит данные параметры не значимы и модель на практике использовать нельзя.
Вследствие полученных выше результатов можно сделать вывод о том, что данное уравнение не используется для прогнозирования. Однако в учебных целях доведем наш анализ до конца.
Далее оценим существенность совокупного коэффициента множественной корреляции на основе F-критерия Фишера по формуле:
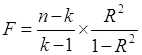
где:
n – число уровней ряда;
к – число параметров;
R – коэффициент множественной корреляции.
После расчета получаем:
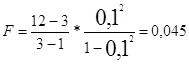
Сравним Fрасч с Fтеор для числа степеней свободы U1 = 9 и U2 = 2, видим, что 0,045 < 19,38, то есть Fрасч < Fтеор - связь признаётся не существенной, то есть корреляция между факторами x1, x2 и у не существенна.
Похожие работы
... к среднегодовой стоимости основных и нормируемых оборотных фондов. Различают два вида рентабельности: рассчитанную на основе балансовой (общей) прибыли и на основе чистой прибыли. 2. Организационно-экономическая характеристика КСП имени Дзержинского Новоайдарского района Луганской области Результаты работы сельскохозяйственных предприятий существенно зависят от условий производства. Поэтому ...
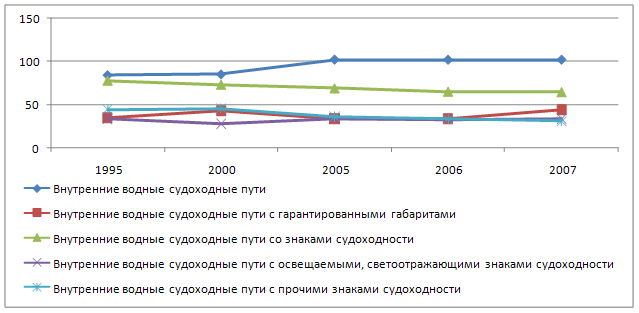
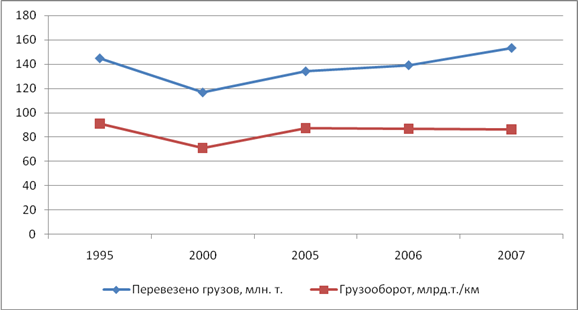
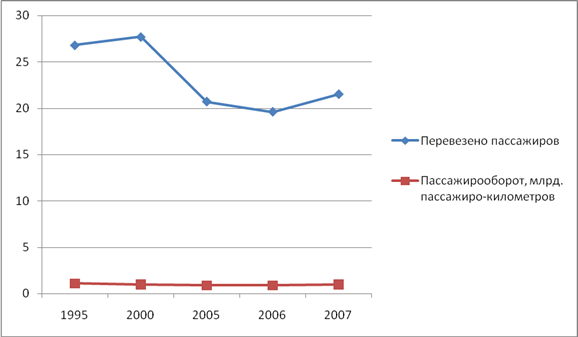
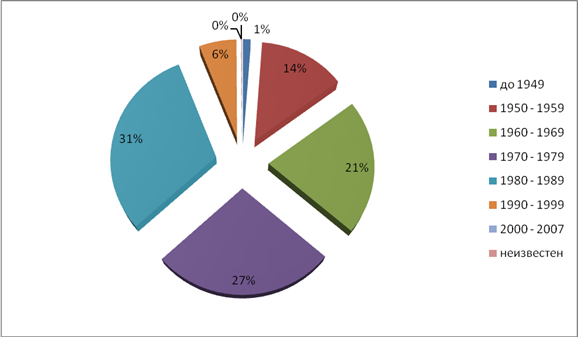
... , а в предыдущие периоды происходило снижение. Таким образом, по результатам проведенного анализа мы видим ухудшение основных показателей деятельности внутреннего водного транспорта в РФ. 2.2 Оценка структуры и динамики структуры экономико-статистических показателей внутреннего водного транспорта Далее проведем анализ структуры и динамики структуры основных показателей развития внутреннего ...
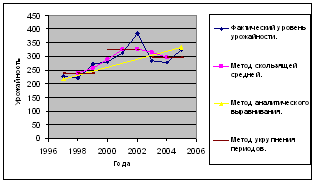
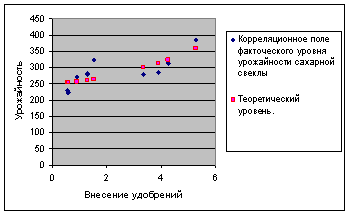
... 0,9 -0,3 Фондоемкость, руб. 0,8 1,0 1,1 +0,3 Производительность труда, тыс. руб. 303,0 310,0 359,7 +56,7 Уровень рентабельности, % +5,7 +7,8 +10 +4,3 3. Экономико-статистический анализ производства сахарной свеклы Экономико-статистический анализ заключается во всестороннем изучении состояния сельского хозяйства, с тем, чтобы сделать выводы о закономерностях его развития и ...
... не выполняется первое равенство абсолютной ликвидности баланса. Это свидетельствует о недостаточном количестве на предприятии наиболее ликвидных активов – денежных средств в наличной и безналичной формах. 3. Проведение статистического анализа при помощи MS Excel 3.1 Описательная статистика Проведем статистический анализ прибыли 15 сельскохозяйственных предприятий Славяносербского района ...
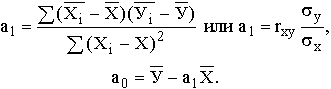
0 комментариев