Навигация
В каких границах следует ожидать размер диаметра, чтобы вероятность невыхода за эти границы была равна р=0,9934
2. в каких границах следует ожидать размер диаметра, чтобы вероятность невыхода за эти границы была равна р=0,9934.
Решение:
1. Для вычисления вероятности того, что диаметр наудачу взятой детали имеет размеры от ![]() до
до ![]() , воспользуемся формулой, по которой найдем вероятность попадания нормальной СВ Х в интервал
, воспользуемся формулой, по которой найдем вероятность попадания нормальной СВ Х в интервал ![]() :
:
![]()
где Ф(х) - функция Лапласа.
Значит вероятность равна:
![]()
По таблице значений функции Лапласа находим: ![]() ,
, ![]() .
.
Значит, ![]()
2. Рассмотрим событие ![]() , где
, где ![]() . Будем считать, что вероятность этого события равна р=0,9934:
. Будем считать, что вероятность этого события равна р=0,9934:
![]()
По условию известно, что а=8 ![]() и
и ![]() .
.
Так как ![]()
Значит, по таблице значений функции Лапласа находим, что ![]() . Следовательно,
. Следовательно, ![]() .
.
Из неравенства ![]() , получаем
, получаем
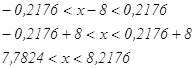
Значит, с вероятностью 0,9934 следует ожидать, что контролируемый размер детали будет заключен в границах от 7,7824 см до 8,2176 см.
Задание 6
В результате статистических наблюдений некоторой совокупности относительно количественного признака Х были получены данные, записанные в виде статистического ряда.
| 22 | 19 | 21 | 21 | 18 | 22 | 19 | 23 | 23 | 16 |
| 22 | 23 | 17 | 23 | 28 | 24 | 22 | 19 | 24 | 20 |
| 24 | 22 | 26 | 21 | 16 | 12 | 19 | 24 | 23 | 21 |
| 26 | 24 | 19 | 14 | 25 | 21 | 26 | 18 | 18 | 28 |
| 21 | 21 | 18 | 17 | 24 | 18 | 31 | 21 | 18 | 22 |
| 21 | 21 | 21 | 19 | 11 | 24 | 16 | 20 | 22 | 15 |
| 25 | 23 | 21 | 22 | 18 | 17 | 19 | 19 | 27 | 13 |
| 23 | 13 | 27 | 24 | 25 | 21 | 24 | 17 | 18 | 19 |
| 24 | 19 | 17 | 24 | 16 | 24 | 24 | 19 | 25 | 20 |
| 21 | 16 | 16 | 20 | 19 |
Требуется:
1. составить дискретный или интервальный ряд распределения частот и относительных частот СВ Х и построить полигон или гистограмму частот;
2. Найти эмпирическую функцию распределения случайной величины и построить ее график.
3. Вычислить числовые характеристики данного эмпирического распределения: среднее значение, дисперсию и среднее квадратическое отклонение.
4. выдвинуть гипотезу о виде распределения рассматриваемой СВ Х. Обосновать выбор вида распределения. Написать аналитическое выражение функции плотности для выбранного распределения, найти теоретические частоты и теоретическую интегральную функцию распределения.
5. приняв уровень значимости 0,05 или 0,01, по критерию согласия Пирсона проверить гипотезу о виде распределения;
6. для подтвердившегося нормального распределения найти вероятность попадания признака в интервал ![]()
Решение:
1. Для построения интервального ряда расположим различные значения признака в порядке возрастания значений. И посчитаем частоту каждого из значений. Получаем таблицу 2.
| xi | mx | xi | mx | xi | mx |
| 11 | 1 | 20 | 4 | 31 | 1 |
| 12 | 1 | 21 | 14 | ||
| 13 | 2 | 22 | 8 | ||
| 14 | 1 | 23 | 7 | ||
| 15 | 1 | 24 | 13 | ||
| 16 | 6 | 25 | 4 | ||
| 17 | 5 | 26 | 3 | ||
| 18 | 8 | 27 | 2 | ||
| 19 | 12 | 28 | 2 |
Таким образом, видим, что xmin=11; xmax=31. Разобьем множество значений выборки на интервалы.
Найдем длину интервала: ![]()
Длина каждого интервала будет равна: ![]()
Таким образом, получаем вариационный ряд:
| интервал | середина интервала, xi | частота, mi | |
| 11 | 15 | 13 | 6 |
| 15 | 19 | 17 | 31 |
| 19 | 23 | 21 | 33 |
| 23 | 27 | 25 | 22 |
| 27 | 31 | 29 | 3 |
| Σ | 95 | ||
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...





0 комментариев