В каких границах следует ожидать размер диаметра, чтобы вероятность невыхода за эти границы была равна р=0,9934
Строим гистограмму и полигон частостей случайной величины
Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости a=0,01
Корреляционное поле Y на X
Навигация
Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости a=0,01
Теория вероятностей
15407
знаков
11
таблиц
13
изображений
5. Проверим гипотезу о том, что данные получены из нормально распределенной генеральной совокупности с уровнем значимости a=0,01.
Составим расчетную таблицу.
| интервал | середина интервала, xi | частота, mi |
|
|
|
| pi | n'i=npi | mi-n'i | (mi-n'i)2 | (mi-n'i)2/n'i | |
| 11 | 15 | 13 | 6 | -1,40 | -0,500 | -0,419 | 0,081 | 7,676 | -1,676 | 2,808976 | 0,365943 | |
| 15 | 19 | 17 | 31 | -1,40 | -0,36 | -0,419 | -0,141 | 0,279 | 26,467 | 4,533 | 20,548089 | 0,776366 |
| 19 | 23 | 21 | 33 | -0,36 | 0,69 | -0,141 | 0,255 | 0,396 | 37,5725 | -4,5725 | 20,90775625 | 0,556464 |
| 23 | 27 | 25 | 22 | 0,69 | 1,73 | 0,255 | 0,458 | 0,203 | 19,3135 | 2,6865 | 7,21728225 | 0,373691 |
| 27 | 31 | 29 | 3 | 1,73 | 0,458 | 0,500 | 0,042 | 3,971 | -0,971 | 0,942841 | 0,237432 | |
|
| Σ |
| 95 |
|
|
|
| 1,000 | 95 |
|
| 2,309896 |
Где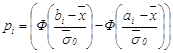 
. Таким образом 
.
По таблице критических точек распределения 
, по уровню значимости 
и числу степеней свободы 
находим критическую точку правосторонней критической области 
.
Так как 
- гипотезу о нормальном распределении генеральной совокупности принимаем.
Теперь для отыскания вероятности попадания признака Х в интервал
(20,37-5;20,37+3)=(15,37;23,37) воспользуемся формулой:
где Ф(х) - функция Лапласа.
У нас
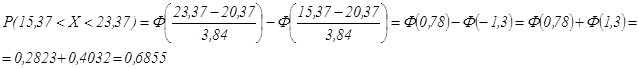
Задание 7
Приводятся результаты наблюдений (хi;yi) над двумерной СВ (Х,У). Используя эти экспериментальные данные, необходимо:
1)определить числовые характеристики выборки 
;
2)условные средние значения величин Х и Y;
3)коэффициент корреляции;
4)параметры эмпирической линейной функции регрессии Y на Х и X на Y и построить их графики;
5)При уровне значимости α=0,05 проверить адекватность линейной регрессии исходным данным.
6)написать выборочные уравнения прямых линий регрессии у на х и х на у;
7)вычислить коэффициент корреляции и проверить гипотезу о значимости коэффициента линейной корреляции при α=0,01;
|
| 5 | 9 | 13 | 17 | 21 | 25 | nу |
| 3 | 3 | 3 | |||||
| 8 | 6 | 7 | 2 | 15 | |||
| 13 | 4 | 10 | 25 |
| 39 | ||
| 18 | 8 | 7 | 4 |
| 19 | ||
| 23 | 5 | 2 | 7 | ||||
| 28 | 3 | 1 | 1 | 2 | 7 | ||
| nх | 3 | 18 | 20 | 37 | 7 | 5 | 90 |
Решение:
Для всех вычислений, составим таблицу:
|
| 5 | 9 | 13 | 17 | 21 | 25 | nх | nхx | nхx2 | |||
| 3 | 3 | 3 | 9 | 27 | ||||||||
| 8 | 6 | 7 | 2 | 15 | 120 | 960 | ||||||
| 13 | 4 | 10 | 25 | 39 | 507 | 6591 | ||||||
| 18 | 8 | 7 | 4 | 19 | 342 | 6156 | ||||||
| 23 | 5 | 2 | 7 | 161 | 3703 | |||||||
| 28 | 3 | 1 | 1 | 2 | 7 | 196 | 5488 | |||||
| ny | 3 | 18 | 20 | 37 | 7 | 5 | 90 | 1335 | 22925 | |||
| nyy | 15 | 162 | 260 | 629 | 147 | 125 | 1338 |
| ||||
| nyy2 | 75 | 1458 | 3380 | 10693 | 3087 | 3125 | 21818 |
| ||||
| XiYj mxy |
| ||||||||||
| 0 | 0 | 0 | 0 | 0 | 225 |
| |||||
| 0 | 0 | 0 | 816 | 1176 | 400 |
| |||||
| 0 | 468 | 1690 | 5525 | 0 | 0 |
| |||||
| 0 | 1296 | 1638 | 1224 | 0 | 0 |
| |||||
| 0 | 1035 | 598 | 0 | 0 | 0 |
| |||||
| 420 | 252 | 364 | 952 | 0 | 0 |
| |||||
| 18079 |
| ||||||||||
1) Найдем средние, дисперсии, исправленные дисперсии, среднеквадратические отклонения:
Найдем выборочные средние
Найдем выборочные дисперсии
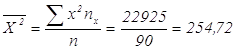
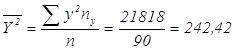
Выборочные среднеквадратические отклонения
2) Найдем условные средние значения величин Х и Y.
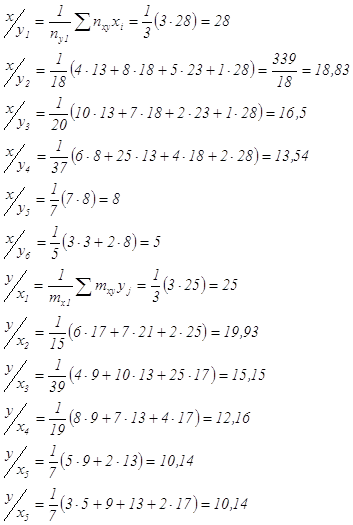
Оформим полученные данные в таблице:
| yj | 3 | 8 | 13 | 18 | 23 | 28 |
|
| 28 | 18.83 | 16.5 | 13.54 | 8 | 5 |
| хi | 5 | 9 | 13 | 17 | 21 | 25 |
|
| 25 | 19.93 | 15.15 | 12.16 | 10.14 | 10.14 |
3) Найдем коэффициент корреляции;
Найдем коэффициент корреляции:
4) Проверим значимость коэффициента корреляции на уровне a=0,01
Вычислим статистику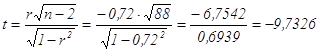 
.
По статистическим таблицам найдем квантиль распределения Стьюдента с
n-2=88 степенями свободы и заданной надежностью a=0,01 – 
. Так как 
, то значение коэффициента корреляции считаем значимым с заданным уровнем надежности.
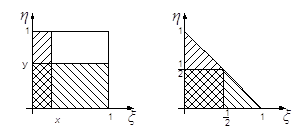
6) Построим корреляционные поля и по характеру расположения точек на нем сделать вывод о типе линии регрессионной зависимости между величинами Х и Y
Отметим точки 
и 
на декартовых системах координат, для этого воспользуемся таблицами, полученными в пункте 2).
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
0 комментариев