Навигация
День показал что нужно покупать
10 день показал что нужно покупать
Задача №3| Сумма | Дата начальная | Дата конечная | Время в днях | Время в годах | Ставка | Число начислений |
| S | TH | TK | Тдн | Тлет | i | m |
| 1500000 | 17,01,02 | 13,03,02 | 180 | 4 | 20 | 2 |
Найти:
3.1.1. Точные проценты с точным числом дней ссуды;
3.1.2. Обыкновенные проценты с точным числом дней ссуды.
3.1.3. Обыкновенные проценты с приближенным числом дней ссуды
Решение:
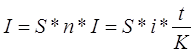
| 3,1) | сумма процентов | |||||
| S-сумма кредита | ||||||
| i-ставка за кредит | ||||||
| n - количество периодов начисления (поскольку проценты годовые, то n = t /K) | ||||||
| t - срок в днях | ||||||
| K - число дней в году | ||||||
а) вычислить точные проценты с точным числом дней ссуды
| K= | 365 |
| S= | 1500000 |
| i= | 20 |
| t= | 56 |
| сумма процентов | 46027,40 |
б) вычислить обыкновенные проценты с точным числом дней
К= | 360 |
| S= | 1500000 |
| i= | 20 |
| t= | 56 |
| сумма процентов | 46666,67 |
в) вычислить обыкновенные проценты с приближенным числом дней
| число месяца когда взял | число месяца когда отдал | разница |
| 17 | 13 | 4 |
| t= | 55 |
| K= | 360 |
| t= | 55 |
| S= | 1500000 |
| i= | 20 |
| сумма процентов | 45833,33 |
3.2) Через Тдн дней подписания договора должник уплатит S рублей. Кредит выдан под i% годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт
Решение:
![]()
Дисконт – разница между тем, что он отдал и тем, что взял – фактически – это сумму начисленных процентов.
| Первоначальная сумма= | 136 364 |
| через Тдн= | 180 |
| должник уплатит S= | 1500000 |
| процентная ставка i= | 20 |
| K= | 360 |
| дисконт = | 1 363 636 |
3.3) Через Тдн предприятие должно получить по векселю S руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i% годовых (год равен 360 дней). Определить полученную сумму и дисконт?
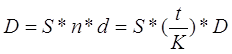
![]()
| Дисконт= | 150000 |
| t=Тдн= | 180 |
| K= | 360 |
| S= | 1500000 |
| d=i= | 20 |
| P= | 1350000 |
3.4) В кредитном договоре на сумму S руб. и сроком на Тлет, зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму?
| P= | 15694117,03 |
| n=Тлет= | 4 |
| i= | 20 |
| S= | 1500000 |
| множ. Наращивания= | 11,46 |
3.5) Ссуда, размером S руб. и предназначена сроком на Т лет. Проценты сложные, ставка i% годовых. Проценты начисляются m раз в году. Вычислить наращиваемую сумму?
![]()
| S= | 1500000 |
| n=Tлет= | 4 |
| m= | 2 |
| %i= | 20% |
| P= | 3215383,215 |
3.6) Вычислить эффективную ставку процента если банк начисляет проценты m раз в году, исходя из номинальной ставки i% годовых
![]()
| m= | 2 |
| %i= | 20% |
| Iэ= | 21,55% |
| 0,21550625 | 21,55063 |
3.7) Определить какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.
![]()
| m= | 2 |
| iэ= | 20% |
| i= | 38,2% |
| 0,38178046 | 38,17805 |
3.8) Через Тлет предприятию будет выплачена сумма S руб. Опрделить ее современную стоимость при условии, что применяется сложная ставка i% годовых?
![]()
| S= | 1500000 |
| n=Tлет= | 4 |
| %i= | 20% |
| P= | 602816,36 |
3.9) Через Тлет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i% годовых. Определить дисконт?
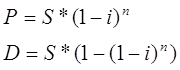
S= | 1500000 |
| n=Tлет= | 4 |
| %i= | 20% |
| современная сумма= | 614400,00 |
| Дисконт= | 885600,00 |
3.10) В течении Тлет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного периода?
![]()
| S= | 1500000 |
| n=Tлет= | 4 |
| %i= | 20% |
| m= | 2 |
| R= | 24 194 601 |
Похожие работы
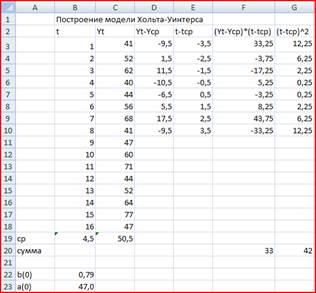
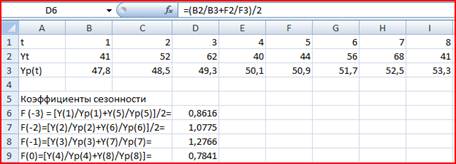
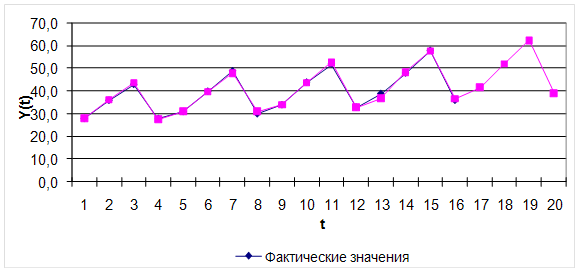
... Квартал 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Вариант 9 41 52 62 40 44 56 68 41 47 60 71 44 52 64 77 47 Решение: 1. Построение адаптивной мультипликативной модели Хольта-Уинтерса: Исходные данные: Таблица 1. t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Y(t) 41 52 62 40 44 56 68 41 47 60 71 44 52 64 77 47 Для оценки начальных ...
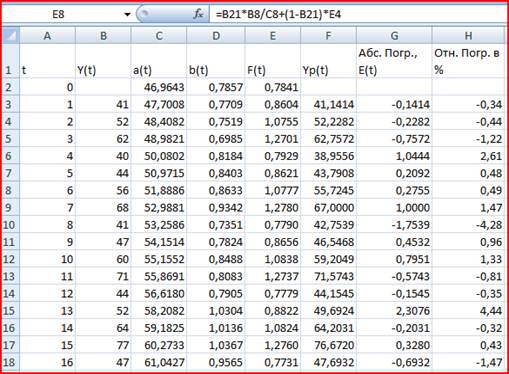
о, что для расчета а(1) и b(1) необходимо оценить значения этих коэффициентов для предыдущего период времени (т.е. для t=1-1=0). Значения а(0) и b(0) имеют смысл этих же коэффициентов для четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 1. Для оценки начальных значений а(0) и b(0) применим линейную модель к первым 8 значениям Y(t) из табл. 1. Линейная ...
... модели строится прогноз на один шаг вперед, причем его отклонение от фактических уровней ряда расценивается как ошибка прогнозирования, которая учитывается в соответствии со схемой корректировки модели. Далее по модели со скорректированными параметрами рассчитывается прогнозная оценка на следующий момент времени и т.д. Т.о. модель постоянно учитывает новую информацию и к концу периода обучения ...
... 2. Сопоставление фактических и расчетных значений по линейной модели t Y (t) Yp (t) 1 43 49,42 2 54 50,26 3 64 51,11 4 41 51,95 5 45 52,80 6 58 53,64 7 71 54,49 8 43 55,33 Коэффициент сезонности есть отношение фактического значения экономического показателя к значению, рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности I ...

0 комментариев