Навигация
Визначення проблем банку. Напрямок майбутніх досліджень
1.4 Визначення проблем банку. Напрямок майбутніх досліджень
Важливе місце в економіці відведена банкам, які регулюють грошовий оборот країни, акумулюють грошові ресурси і перерозподіляють їх. В процесі своєї активної діяльності банки стикаються з різного роду ризиками. Неефективне управляння ризиками в банківський діяльності може привести к банкрутству, а в силу його положення в економіці, і к цілому ряду банкрутств, зв’язаних з ним виробництв, банків та фізичних осіб.
Основним видом діяльності банка є кредитна, яка включає в середньому 50% доходності усіх активів, і як правило, висока доходність супроводжується підвищеним ризиком.
Приоритетні напрямки розвитку АКБ „Правекс-Банк”:
Споживче кредитування, кредитна картка „Росрочка”;
Пластикові картки – ЗК, часні, кредитні(універсальні, кредит під депозит, кредит під зарплату);
Рознічні послуги (обмін валют, „Правекс-Телеграф”, „обмін ветхої валюти”);
Продаж банківських металів, продаж іноземних монет;
Залогове кредитування;
Риночні послуги страхування( обов’язкове страхування граждансько-провової відповідальності власників транспортних средств)
З збільшенням об’ємів кредитування стає актуальними і задачі управляння кредитним ризиком банку. В зв’язку з цим розробка методів оцінки та механізму регулювання кредитного портфельного ризику забезпечує укріплення фінансового положення банку.
Недостатній рівень розвитку теоретичних та методологічних питань портфельного аналізу ризиків кредитних операцій в системі аналізу банківської діяльності обусловлює вибір теми роботи і свідчать о її актуальності.
Метою даної роботи є розробка економічно обоснованого механізму оцінки і регулюванні кредитним портфельним ризиком з метою задоволення інтересів банку, пов’язаних з мінімізацією ризику кредитного портфелю банка та підвищення доходності портфеля. Об’єктом даної роботи є кредитна діяльність банка, а також кредитний ризик, як основна частина кожної банківської операції. Відповідно до сучасних наукових підходів ця проблема може бути вирішена за допомогою математичних методів.
2. ЗАСТОСУВАННЯ ЕКОНОМІКО-МАТЕМАТИЧНИХ МЕТОДІВ
2.1 Методологічні підходи і проблеми щодо здійснення трансакцій
Якщо йдеться про оптимізацію траси платежів, то починати потрібно з транспортної задачі лінійного програмування, за допомогою якої загалом і здійснюється вибір найкращого шляху, в нашому випадку – фінансових платежів, при заданих умовах і обмеженнях.
2.1.1 Постановка транспортної задачі
Транспортна задача лінійного програмування формулюється так. Маємо m пунктів відправлення або банківських рахунків А1, А2,..,Аm, у яких знаходяться фінансові запаси відповідно а1, а2,..,аm припустімо, євро. Крім того, є n пунктів призначення – банків кореспондентів В1, В2,...,Вn, в яких існують кореспондентські рахунки для отримання b1, b2,...,bnгрошових одиниць. Передбачається, що сума всіх переказів дорівнює сумі на таких рахунках, тобто
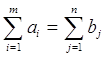 . (2.1)
. (2.1)
Позначимо сij вартість переказу суми від кожного пункту відправлення, тобто нашого банку Аi до кожного пункту призначення Вj. Матриця вартостей С має вигляд
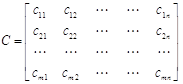 . (2.2)
. (2.2)
Потрібно скласти такий план переказів, при якому всі заявки були б виконані й загальна вартість усіх переказів була мінімальною. Таким чином, у якості критерію обрана вартість перевезення вантажу. Критеріями в транспортній задачі можуть бути такі показники: відстань, час, потужність та ін. Транспортна задача, в якій виконується умова, називається закритою. Задача, у якій ця умова не виконується, називається відкритою.
Ми будемо розглядати саме такий випадок, бо 95% усіх крупних банківських переказів здійснюються строго з одного рахунку на інший.
Математичне формулювання транспортної задачі може бути подано у такому вигляді: нехай xij – об’єм переказу, що відправляється з i-го пункту відправлення Аi в j-й пункт призначення Вj (![]() ), xij³ 0. Змінні xij повинні задовольняти нерівностям (2.3. – 2.9.).
), xij³ 0. Змінні xij повинні задовольняти нерівностям (2.3. – 2.9.).
Будь-яку сукупність значень xij ( ![]() ) називають планом переказів. План, що задовольняє умовам (2.3) - (2.9), називають припустимим. Ранг системи (2.3) - (2.8) дорівнює r = m + n - 1, тоді в ній (m + n - 1) базисних та (m-1)(n-1) вільних змінних. Тому план, у якому відмінно від нуля не більш m + n - 1 змінних, а інші рівні нулю, називають опорним.
) називають планом переказів. План, що задовольняє умовам (2.3) - (2.9), називають припустимим. Ранг системи (2.3) - (2.8) дорівнює r = m + n - 1, тоді в ній (m + n - 1) базисних та (m-1)(n-1) вільних змінних. Тому план, у якому відмінно від нуля не більш m + n - 1 змінних, а інші рівні нулю, називають опорним.
Оптимальний план - це такий план, що серед усіх припустимих має найменшу вартість перевезень. Пошук оптимального плану виконується за допомогою транспортної таблиці 2.1.
Вартість переказу ![]() поміщають у правому верхньому куті клітин таблиці. Клітини таблиці, у яких будемо записувати відмінні від нуля перевезення
поміщають у правому верхньому куті клітин таблиці. Клітини таблиці, у яких будемо записувати відмінні від нуля перевезення ![]() , називаються базисними. Таких клітин не більш ніж m+n-1. Порожні клітини називаються вільними, їх не менше (m-1)(n-1).
, називаються базисними. Таких клітин не більш ніж m+n-1. Порожні клітини називаються вільними, їх не менше (m-1)(n-1).
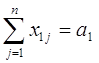 (2.3)
(2.3)
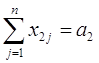 (2.4)
(2.4)
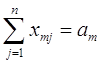 (2.5)
(2.5)
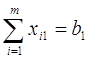 (2.6)
(2.6)
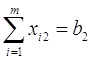 (2.7)
(2.7)
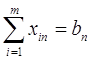 (2.8)
(2.8)
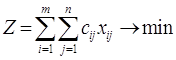 . (2.9)
. (2.9)
Таблиця 2.1 – Транспортна таблиця
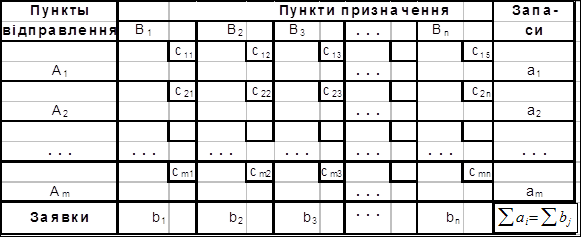
Усі подальші дії по вирішенню транспортної задачі будуть зводиться до перетворення транспортної табл. 2.1, тобто до двох етапів:
а) відшукування першого розв'язання методом „північно-західного кута”;
б) пошуку оптимального розв'язання задачі за допомогою методу потенціалів.
Проте перед нами стоїть завдання залучити до математичної моделі такі обмеження, які неможливо задати в рамках транспортної задача, тому доцільним є використання іншого методу оптимізації – методу Ньютона.
0 комментариев