Застосування теорії Марковіца для формування банківських активів з точки зору оптимізації прибутку

2.2 Застосування теорії Марковіца для формування банківських активів з точки зору оптимізації прибутку

В наш час банківський ринок пропонує все більше і більше різноманітних видів кредитних пакетів. Завдяки засобам телекомунікацій, видача кредитів стала міжнародним явищем. Кожен тип кредиту має свою доходність, яка з часом коливається, тому вибір тих типів кредитів, які варто включити у власні активи, складає певну проблему.

Ця проблема вирішується за допомогою найбільш відомої моделі портфелю цінних паперів Марковіца, для якої може бути знайдено оптимальне рішення за допомогою методів лінійного програмування для:

-           Максимуму доходів при заданому значенні ризику

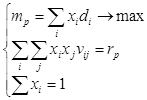, (2.21)

-           Мінімуму ризику при заданому значенні доходності

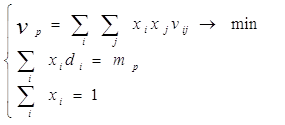, (2.22)

де x_i– частка капіталу i-го виду, d_i- середня прибутковість i-го виду у відсотках в розрахунку на одну грошову одиницю, m_p – задана середня прибутковість, v_ij – ковариація доходностей i – го та j – го видів, v_р– ковариація, якою вимірюється ризик, rp – задана середня коваріація.

Ця модель широко застосовується зараз і для розрахунку ефективності інвестиційних проектів. Але це використання провадиться без критичного аналізу можливої межі застосування моделі виду (2.21)-(2.22).

В зв’язку з вищесказаним, виникають наступні задачі:

·          виявлення можливості використання матриці коефіцієнтів кореляції 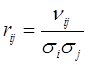, (де – середнє квадратичне відхилення доходності) замість матриці коваріації. Коефіцієнт кореляції є безрозмірним і завжди коливається в межах [±1], що робить його значно зручнішим для аналізу ситуації та визначення допустимого рівня ризику, аніж коваріація. Особливо це стосується моделі (2.2.1), де потрібно задавати певний, наперед визначений рівень ризику;

·          проведення аналізу по типу матриці коваріації – для якого типу це рішення можливе чи існує?

·          і останнє, чи не можна спростити моделі (2.21)-(2.22) і звести їх у єдину модель виду

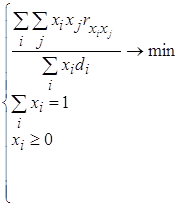, (2.23)

щоб не задумуватися над проблемою визначення допустимого рівня ризику для кожного портфелю. В (2.23) якості цільової функції вибрано відношення, в якому середній ризик поділено на середню доходність портфелю. Очевидно, що така цільова функція має прагнути мінімуму. Назвемо таку модель “ризиково-доходною”

Рішення поставлених задач виконувалося із застосуванням функцій СЛУЧМЕЖДУ, “Ковариация”, “Корелляция” та “Поиск решения” електронних таблиць Excel.

На підставі експериментів можна зробити наступні висновки щодо оптимальної моделі портфелю цінних паперів Марковіца:

·          Використання матриці кореляцій дає тотожні результати з використанням матриці коваріацій.

·          Найбільш ефективним є портфель, який складається зі слабокорельованих кредитів

·          “Ризиково-доходна”.модель виду може бути застосована для випадку, коли складно визначитися з допустимими рівнями ризику чи доходності за моделями виду

·          Результати оптимальних розрахунків за моделлю варто приймати для випадків, коли модифікований ризик не перевищує 1.

2.3 Поняття оптимального балансу. Критерій оптимальності. Побудова оптимального балансу на підставі фінансових коефіцієнтів

Нехай існують деякі статті балансу підприємства, куди входять і статті звіту про збитки та прибутки по ф.2, СБі (1≤ і ≤ N, де N – кількість таких статей балансу), які пов’язані одна з одною кореспондентськими відносинами вигляду

СБі = Fl(СБj) ( 1≤ і, j ≤ N, i≠ j, 1≤ l ≤ K ), (2.24)

де K – кількість кореспондентських зв’язків для даного балансу, Fl – функція кореспондентських (для балансу) або розрахункових зв’язків (для ф.2). Нехай також, існує множина фінансових коефіцієнтів, які виводяться зі статей балансу шляхом утворення з них певних комплексів вигляду

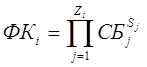, (2.25)

де 1≤ і ≤ М, М – кількість фінансових коефіцієнтів, Zi – кількість статей балансу, які входять до i – го коефіцієнту, Sj – дорівнює “1” або “–1”. На підставі досліджень відомо, що для кожного з цих коефіцієнтів існує певна межа їх значень, більше або менше якої баланс стає неефективним, тобто

,(2.26)

де ОБі – значення цих обмежень для і-го коефіцієнта. Y=0, якщо обмеження вимагають, щоб коефіцієнт був менший за них: Y=1, якщо більший.

Нехай в процесі диверсифікації капталу були запропоновані декілька інвестиційних проектів, реалізація яких має призвести до зміни окремих статей балансу у вигляді

СБні=СБі + ІПі, (2.27)

де СБні нове значення статті балансу після запровадження чергової пропозиції інвестиційного проекту ІПі. Тут мається на увазі, що в модель підставляються одразу всі можливі варіанти інвестиційних проектів.

Якщо ІПі не пов’язане з іншими ІПі , то його значення треба обмежувати як