Два отрезка называются равными, если они имеют одинаковую длину

4.         Два отрезка называются равными, если они имеют одинаковую длину.

5.         Треугольники равны, если у них соответствующие стороны и соответствующие стороны углы равны.

Рассмотрим методику изучения основных свойств.

1)         Основные свойства принадлежности.

1,а) Какова бы ни была прямая, существуют точки, принадлежащие прямой.

1,б) Через любые две точки можно провести прямую, и только одну.

Наглядное введение аксиом сопровождается логическим анализом их формулировок, необходимый для выяснения точного математического смысла каждой аксиомы. Анализ поправляется вопросами:

О каких геометрических фигурах говорится в основном свойстве 1,а)? Что именно говорится о прямых и точках? Сколько утверждений сформулировано в основном свойстве 1,а)? Сформулируйте их по отдельности. Какими другими словами “какова бы ни была прямая”? (“Для любой прямой” и “для каждой прямой”)

Закрепление практических навыков построения прямых и точек и усвоение соответствующей математической терминологии могут быть осуществлены с помощью математического диктанта:

1.         Постройте прямую а. Отметьте точки А и В, принадлежащие прямой а. Постройте С и Д, не принадлежащие прямой а.

2.         Постройте две пересекающиеся прямые c и d. Обозначьте буквой А точку пересечения этих прямых. Постройте точку В, принадлежащую прямой с, но не принадлежащую прямой d. Отметьте точку С, принадлежащую прямой d, но не принадлежащую прямой с.

2)         Основные свойства расположения.

2,а) Из трех точек на прямой одна, и только одна, лежит между двумя другими.

2,б) Прямая разбивает плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекается с прямой. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекается с прямой.

Методическая схема введения аксиом:

1)         ввести аксиому на наглядной основе;

2)         сформулировать аксиому;

3)         выполнить логический нализ формулировки аксиом;

4)         провести математический диктант.

3)         Основные свойства измерения отрезков и углов.

3,а) Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длины частей, на которые он разбивается любой своей точкой.

3,б) Каждый угол имеет определённую длину, большую нуля. Развёрнутый угол равен . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

4)         Основные свойства откладывания отрезков и углов.

4,а) На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.

4,б) От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, и только один.

4,в) Каковы бы ни были треугольник и полупрямая, существует треугольник, равный данному, у которого первая вершина лежит в начале полупрямой, вторая – на полупрямой, а третья – в заданной полуплоскости относительно полупрямой и её продолжения.

Конкретно-индуктивным методом следует пользоваться лишь при изучении трудных для понимания аксиом. Рассмотрим один из вариантов введения аксиомы 4,в).

Начертим: , полупрямую ; отметим полуплоскость относительно .(полупрямой и её продолжения)

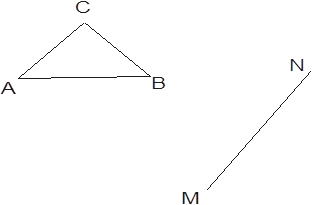
Вопрос: Можно ли построить , равный , который бы распологался следующим образом:

а) вершина  совмещалась бы с началом  полупрямой ;

б) вершина  лежала бы на полупрямой ;

в) вершина  лежала бы в заданной полуплоскости относительно полупрямой  и её продолжения?

 будем “строить” с помощью картонной модели . Построение направляем вопросами:

Что дано?(, полупрямая , полуплоскость); Что требуется построить? Каким четырём условиям должен удовлетворять ? Покажите, как можно построить такой  с помощью нашей модели. После построения делаем вывод.

5) Основное свойство параллельных прямых.

Через точку не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Использованная методическая форма приведения аксиом в учебнике Погорелова впервые была дана в учебнике Киселёва, а именно:

Аксиомы формулируются, но без внешнего подчеркивания формально-логического аспекта(они не нумеруются, не сообщаются названия групп). Формально-логический аспект не подчеркивается и в первых доказательствах. Непосредственные ссылки на аксиомы в этих доказательствах не делаются(они подразумеваются и при необходимости в устном изложении на уроке могут быть сделаны). Такому приёму свойственны неформальный стиль изложения и активное обращение к наглядности в первых доказательствах. Ссылки в доказатьльствах появляются после изучения признаков равенства треугольников. Подобная “маскировка” аксиом позволяет на первый план выдвинуть наглядно-геометрическую(содержательную) сторону доказательств, которые при этом тесно связываются с возможными интуитивными рассуждениями учащихся.

В учебнике Погорелова, в отличии от приведенного изложения по Киселёву, предпринята попытка формализации начала курса(чёткое выделение аксиом, ссылок в первых доказательствах)

2. Методика введения понятий и теорем в курсе геометрии

Ряд математических понятий является неопределенным. В учебнике Погорелова к ним отнесены: точка, прямая, точка принадлежащая прямой; “точка В лежит между точками А и С”; “полуплоскость”, “длина отрезка”, “мера угла”, “отложить отрезок(угол) заданной меры”. Свойства неопределяемых понятий описываются аксиомами. Все остальные понятия – определяемые.

Отметим особенности некоторых определений:

1)отрезок определяется таким образом, что концы ему не принадлежат; в связи с этим нельзя использовать обозначение с помощью квадратных скобок; 2) полупрямая определяется т.о., что начальная точка ей не принадлежит; 3) угол определяется так, что вершина угла не принадлежит ему; 4) вершины треугольника (но определённого) принадлежат ему:

“Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - сторонами”.

“Углом называется фигура, которая состоит из точки - вершины угла – и двух различных полупрямых, исходящих из этой точки - стороны угла”.

Одним из центральных понятий для всего курса геометрии является понятие равных треугольников. В учебнике Киселёва равенство треугольников определяется с помощью положения. В пособии Погорелова А.В. сразу вводится общие понятия равенства фигур (с помощью перемещения). Определение равенства треугольников, по учебнику Погорелова (первые издания) для школьной практики новые, т.к.

“Треугольники  и  называются равными, если у них .” Как видно из этого определения, речь идет о равенстве не просто каких-либо двух треугольников, а треугольников, между которыми установлено соответствие: , по этой причине, например, равенство = может выполняться, но для “тех же” треугольников равенство: = может оказаться несправедливым. ”

В действующем пособии Погорелова А.В. используется следующее определение равенства треугольников:

“Треугольники называются равными, если у них соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон”.

3. Методическая схема изучения признаков равенства треугольников

Систематический курс геометрии начнем изучать в 7 классе со знакомства с основными свойствами простейших геометрических фигур, которые сформулированы в виде аксиом.

№ 47, стр.23

АС и ВС пересекаются, т.е. точка В лежит в одной полуплоскости, а точка А – в другой (?)

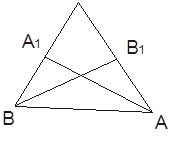Точка В₁ (АС) и лежит между точками А и С

Точка А₁ (ВС) и лежит между точками В и С

Рассмотрим прямую (АА₁), тогда точки А и С принадлежат разным полуплоскостям, т. к. отрезки АС и ВС пересекаются. Поэтому точки В и В₁ (т.к. В₁ лежит между С и А) лежат в разных полуплоскостях и, следовательно, АА₁ ВВ₁

При решении используется понятие полуплоскости и аксиома IV (см. страница 8)

После изучения §1 учащимся даются понятия: аксиомы, теоремы, приводятся простейшие формы доказательств. (прочитать пункт 13 «аксиомы», страница 19) № 22 § 2, страница 32

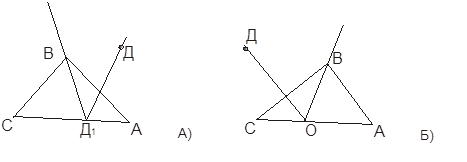Воспользуемся т. 1.1. (стр.17), согласно которой, из того что пересечена одна из сторон ∆ АВС (СА), прямая пересечет еще одну из оставшихся двух.

Рассмотрим ДОА. Если ДОА < АОВ, то луч ОД лежит между лучами АО и ОВ и, следовательно, пересекает отрезок АВ.

Если ДОА > ВОА, то луч ОД пересечет отрезок ВС (это связано

Следующими условиями: ВОА <  ДОА и луч ОД лежит между лучами ОС и ОВ.

Методика изучения признаков равенства треугольников.

Изложение вопросов о равенстве треугольников во многом зависит от выбора определения равных треугольников. В учебнике Погорелова А.В. приводится гильбертовское определение равенства треугольников, которое требует выполнения шести равенств: трех для соответственных сторон треугольников и трех для соответственных углов этих треугольников. (смотри определение равенства на стр. 14)

Рассмотрим еще один вариант изложения темы равные треугольники:

1.         Для равенства двух треугольников потребуем (по определению) равентсов трех соответствующих сторон этих треугольников;

2.         В качестве аксиомы примем следующие утверждения: «Если две стороны и угол, заключенный между ними одного треугольника соответственно равны двум сторонам и углу заключенному между ними, другого треугольника, то такие треугольники равны».

Такой подход позволяет не доказывать третий признак равенства треугольников (это предусмотренно в 1.) и I признаках равенства треугольниках (это аксиома), что приводит к сокращению теоретического материала и упрощению логической структуры темы «Равенство треугольников», позволяет кратчайшим путем ввести один из основных методов традиционно-синтетической геометрии – метод равных треугольников.

Методика изучения первого признака равенства треугольников. Методическая схема по Погорелову А.В.:

1.         Построить два треугольника, у которых равны две пары соответствующих сторон и углы, заключенные между ними;

2.         На основании полученного рисунка сформулируйте теорему записать ее условие и заключение;

3.         Сообщить идею доказательства;

4.         Сообщить план доказательства;

5.         Провести доказательство с четким выделением его шагов;

6.         Осуществить закрепление его доказательства;

7.         Рассмотреть с учащимися задачи на примере признака.

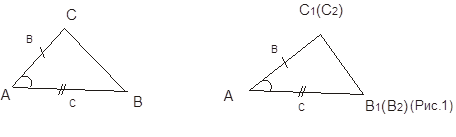Итак, пусть по сторонам В, С и углу А с помощью транспортира и линейки построено два треугольника: ∆ АВС и ∆ А₁В₁С₁

Что можно сказать о ∆ АВС и ∆ А₁В₁С₁ ?

После о том, что эти треугольники равны, формулируем теорему. Выясняем: что дано в этой теореме, а что надо доказать. Рядом с рисунком 1 краткую запись теоремы:

Дано: АВ =А₁В₁; АС=А₁С₁; А = А₁

Доказать: ∆ АВС = ∆ А₁В₁С₁

Сообщаем ученикам идею доказательства: рассмотреть третий ∆ А₁В₂С₂, который: 1. равен ∆ АВС и расположен таким образом, что 2. его вершина В₂ лежит на полупрямой А₁В₁; 3. вершина С₂ находится в той же полуплоскости относительно прямой А₁В₁, в которой лежит вершина С₁.

Теорема будет доказана, если установлено, что ∆ А₁В₂С₂ совпадает с ∆ А₁В₁С_1.

Составляем план доказательства:

1.         Рассмотрим ∆ А₁В₂С₂, о котором говорилось выше;

2.         Докажем, что вершина В₂ совпадает с вершиной В₁;

3.         Докажем, что луч А₁С₂ совпадает с лучом А₁С₁;

4.         Докажем, что вершина С₂ совпадает с вершиной С₁;

5.         Сделаем заключение о равенстве ∆ АВС и ∆ А₁В₁С_1.

Приводим краткую запись доказательства на доске (оно выполняется учителем по ходу изложения, записывать доказательство в тетрадях не нужно),

1) ∆ А₁В₂С₂ = ∆ АВС аксиома IV₃

2) т.к. А₁В₁ = А₁В₂, то В₂ совпадает с В₁ аксиома IV₁

3) т.к. В₁А₁С₁ = В₂А₁С₂, то лучи А₁С₂ и А₁С₁ совпадают

 аксиома IV₂

4) т.к. А₁С₁ = А₁С₂, то точки С₂ и С₁ совпадают аксиома IV₁

5) ∆ А₁В₂С₂ и ∆ А₁В₁С₁ совпадают п.п. 2,4

6) ∆ АВС = ∆ А₁В₁С₁  п.п. 5,1

Вопросы для закрепления

1.         Как был выбран ∆ А₁В₂С₂?

2.         Почему вершина В₂ совпадает с вершиной В₁ ?

3.         Зачем нужно доказывать совпадения лучей А₁С₂ и А₁С₁ ?

4.         Почему вершина С₂ совпадает с вершиной С₁ ?

5.         Почему делается вывод о равенстве ∆ АВС и ∆ А₁В₁С₁

Рассмотрим еще одну методическую схему изучения этого признака: