Рассмотреть решение ряда подготовительных задач;

1.         рассмотреть решение ряда подготовительных задач;

2.         доказать первый признак рав-ва треугольников.

Подготовительные задачи:

1)         отрезки А₁В₁ и А₁В₂ равны отрезку АВ и отложены на полупрямой А₁В_1. Что ещё можно сказать о расположении отрезков А₁В₁ и А₁В₂ ?

2)         Углы В₁А₁С₁ и В₁А₁С₂ равны углу А. Что можно сказать о расположении углов В₁А₁С₁ и В₁А₁С₂ ? Что можно сказать о расположении лучей А₁С₁ и А₁С₂, если они находятся в одной полуплоскости относительно прямой А₁В₁?

3)         Треугольники А₁В₁С₁ и А₁В₂С₂ равны, вершина В₂ лежит на полупрямой А₁В₁, вершина С₂ лежит в одной полуплоскости (относительно прямой А₁В₁) с вершиной С₁. Докажите, что эти треугольники совпадают, т.1. вершинаВ₂ совпадают с вершиной В₁, вершина С₂ – с вершиной С₁.

Рассмотренная первой методическая схема доказательства основана на применении репродуктивного метода обучения и он наиболее эффективен при изучении третьего признака равенства треугольников, наиболее сложного.

Схема решения задач па данной теме:

1)         ученики читают задачу один – два раза, выполняют рисунок, записывают условие и требования задачи. Рассказать о требованиях к построению чертежей при решении задач по планеметрии.

2)         Учитель направляет разбор задачи вопросами: “Что дано в задаче?”, “Что говорится о таком – то треугольнике?”, “Что ещё дано?”, “Что требуется выполнить в задаче?”, “С чего начнем выполнение рисунка?”, “Что ещё надо нарисовать?” и т. д.

3)         Далее приступаем к поиску решения задачи:

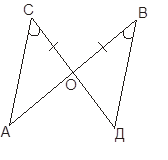Рассмотрим некоторые задачи. №5, §3, стр.45

Дано:

Доказать:

Доказательство:

У данных треугольников есть по одной равной паре соответствующих сторон и одному равному углу прилежащему к этой стороне. Для док-ва рав-ва треугольников по II признаку следует найти ещё пару равных углов  - как вертикальные  по II признаку рав-ва треугольников.

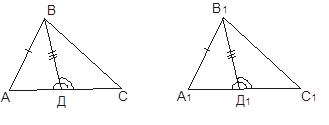
№32, §3, стр.47 Дано: А, В, С, Д лежат на одной прямой;

Доказать:

Доказательство:

1) ;

2)  - по I признаку равенства треугольников;

3) ;

4) - по I признаку равенства треугольников;

№39, §3, стр.48

Дано:

Доказать:

Доказательство:

1)  (по условию); (по условию);  - по III признаку равенства треугольников;

2) ;

3) - по I признаку равенства треугольников;

4)  и  - по III признаку равенства треугольников;

Ч.т.д.

Заключение

Традиционно-синтетические аспекты занимают ведущее положение в геометрии, служат основой изложения остального материала, способствуют формированию пространственного представления и воображения учащихся (недаром некоторые разделы традиционно-синтетической геометрии(параллельность, перпендекулярность прямых и плоскостей, жесткость треугольника) называют “строительной геометрией”).

Придавая темам: параллельные и перпендикулярные прямые, признаки равенства треугольников, свойства равнобедренного и равностороннего треугольников, окружность, описанная около треугольника (вписанная в треугольник), задача на построение; четырёхугольники, правильные многоугольники, излагаем традиционно, максимальные образовательные цели, можно увидеть в них начала систематического курса геометрии.

В качестве вспомогательного математического метода к традиционно-синтетическому рассматривается координатно-векторный метод. Подготовка к вспомогательному методу выражается в раннем введении системы координат в ознакомлении учащихся с примерами решения задач координатным или векторно-координатным методом, в использовании формул расстояния между точками, если отказаться от координатно-векторного метода. Одновременное введение традиционно-синтетического и координатного методов в начале курса может быть обеспечено применением аксиоматически смешанного типа, причем неизбежно избыточной. Аксиоматику, в этом случае, следует рассматривать как инструмент рационализации логико-математической системы учебника.

Литература

1. К.О. Ананченко «Общая методика преподавания математики в школе», Мн., «Унiверсiтэцкае»,1997г.

2.Н.М.Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.

3.Г.Фройденталь «Математика как педагогическая задача»,М., «Просвещение», 1998г.

4.Н.Н. «Математическая лаборатория», М., «Просвещение», 1997г.

5.Ю.М.Колягин «Методика преподавания математики в средней школе», М., «Просвещение», 1999г.

6.А.А.Столяр «Логические проблемы преподавания математики», Мн., «Высшая школа», 2000г.