Організація позакласної роботи з математики

Зміст

Вступ

Розділ 1. Теоретичні основи дослідження

1.1 Психолого-педагогічні передумови організації позакласної роботи з математики

1.2 Види позакласних занять з математики

1.3 Стан досліджуваної проблеми в теорії і практиці навчання математики

Розділ 2. Методика організації позакласної роботи з математики в початкових класах

2.1 Особливості методики позакласної роботи з математики в початкових класах

2.2 Розробка і обґрунтування системи позакласних занять у формі годин цікавої математики

2.2 Організація експериментального дослідження та його результати

Висновки

Список використаної літератури

Додатки

Додаток 1

Додаток 2

Додаток 3

Додаток 4

Додаток 5

Вступ

Формування в учнів навичок самостійної діяльності, творчого потенціалу і здатності використовувати знання на практиці є важливим завданням сучасної української національної школи. У розвитку названих якостей особистості молодшого школяра велике значення має позакласна робота, зокрема позакласна робота з математики.

Дуже часто цей вид навчання й виховання проводиться в старших класах. Чомусь вважається, що молодші учні до неї ще не доросли. Та таке твердження є безпідставним. Адже саме в цьому віці діти найглибше й з найбільшою цікавістю пізнають світ. Вони, як показує неодноразовий досвід педагогів, з величезним задоволенням займаються математикою в позаурочний час. В такий спосіб діти не лише краще пізнають навколишній світ, а й розвивають мислення, вчаться аналізувати, порівнювати і зіставляти, узагальнювати, конкретизувати, абстрагувати від часткового, робити умовиводи. Звісно, вчитель на уроці не може охопити розвиток цих вмінь у всіх дітей, він не встигає також і виховувати всіх учнів в правильному напрямку на класних заняттях. А коли дитина, за своїм власним бажанням, відвідуватиме математичні позакласні заходи, то вона й на уроках буде більш зацікавлено ставитись до навчального матеріалу, вона краще розумітиме й засвоюватиме його. Відповідно й покращаться її результати навчання з інших предметів загалом та математики зокрема.

Та, нажаль, вивчення досвіду роботи вчителів показує, що в реальному навчальному процесі позакласна робота з математики у початкових класах нерідко використовується епізодично, безсистемно, з недостатнім врахуванням вікових особливостей.

Проаналізувавши методичну літературу з позакласної роботи, ми зробили висновок, що її досить для того, аби проводити позакласні заняття систематично, з врахуванням вікових особливостей учнів і методично правильно. Та позакласна робота з математики у початкових класах не повністю ведеться не через те, що немає методичних вказівок й зразків її проведення, а через небажання вчителів робити це (з різних, вагомих на це причин). Сумно, але така робота не сприяє всебічному розвитку молодої особистості.

Саме випадковий характер позакласної роботи з математики або й повна її відсутність у навчанні молодших школярів зумовили вибір теми дипломного дослідження: "Організація позакласної роботи з математики в початкових класах".

Об’єкт дослідження - процес навчання математики учнів початкової школи.

Предмет дослідження - методична система проведення годин цікавої математики у молодших школярів.

В основу дослідження була покладена гіпотеза:

Вплив годин цікавої математики на розумовий і математичний розвиток учнів та на засвоєння математичних знань буде вагомим за рахунок використання цікавого теоретичного матеріалу та нестандартних завдань у позаурочний час.

Мета дослідження - розробити і науково обґрунтувати систему годин цікавої математики та експериментально перевірити умови ефективного впливу їх на загальний та математичний розвиток молодших школярів, покращення результатів навчання.

Для реалізації мети і перевірки гіпотези дослідження необхідно було розв’язати такі завдання:

Вивчити стан досліджуваної проблеми в педагогічній теорії і практиці.

Сформулювати вимоги до системи годин цікавої математики.

Розробити систему годин цікавої математики з молодшими школярами.

Перевірити ефективність запропонованої системи.

Для розв’язання поставлених завдань було використано комплекс методів дослідження: теоретичний аналіз психолого-педагогічної і методико-математичної літератури з проблеми дослідження; вивчення й узагальнення педагогічного досвіду; цілеспрямовані спостереження, анкетування; констатуючий та формуючий експеримент.

Апробація та впровадження результатів дослідження здійснювались у ході дослідно-експериментальної роботи в 3-Г та 3-А класах Тернопільської ЗОШ №23.

Структура та обсяг дипломної. Робота складається із вступу, двох розділів, висновків, списку використаних джерел, які містять 25 позицій, 2 малюнків, 2 таблиці та 5 додатків. Загальний обсяг дипломної роботи - 79 сторінок.

Розділ 1. Теоретичні основи дослідження 1.1 Психолого-педагогічні передумови організації позакласної роботи з математики

Зацікавити учнів математикою, показати її могутність і красу, примусити полюбити її - завдання кожного вчителя початкових класів. Досвідчені вчителі створюють на кожному уроці позитивний емоційний фон, настрій, який полегшує сприймання будь-якого матеріалу. Уміння бачити цікаве й дивуватися приносить дітям радість, породжує творчі поривання, розвиває уяву, що особливо важливо на уроках математики. Таке вміння потрібно виховувати і розвивати в учнів систематично як на уроках, так і в позакласній роботі з математики.

Позакласна робота з математики є складовою частиною всього навчального процесу, природним продовженням роботи на уроці. Позакласна робота має характер математичних розваг, ігор, змагань. Тут широко використовують вправи і завдання у цікавій формі. Однак, стимулюючи цікавість, треба пам’ятати, що вона цінна лише тоді, коли сприяє розумінню математичної суті питання, уточненню і поглибленню знань з математики.

Потреба у позакласній роботі з математики виникла у зв’язку з такою методичною проблемою математичної освіти молодших школярів як взаємозв’язок математичного розвитку і формування логічних прийомів розумових процесів. Розглянемо її докладніше.

Цій проблемі приділяли увагу З.А. Михайлова, Л.А. Венгер, А.А. Столяр, А.З. Зак. В методиці під формуванням логічного мислення дитини розуміють розвиток логічних операцій розумової діяльності, а також вміння розуміти, прослідковувати причинно-наслідкові зв’язки явищ, будувати на їх основі найпростіші висновки. В літературі логічні прийоми розумової діяльності - порівняння, узагальнення, аналіз, синтез, класифікація, аналогія, систематизація, абстрагування - називають також логічними прийомами мислення. Їх формування важливе для дитини як з загально-розвиваючої точки зору, так і для розвитку безпосередньо процесу мислення.

Практично всі досліди психологів, тема яких - аналіз способів та умов розвитку мислення дитини, свідчать: методичне керівництво цим процесом не лише можливе, але й високоефективне. Іншими словами, спеціальна робота, ціль якої - формування логічних прийомів мислення, значно підвищує результативність процесу навчання, незалежно від початкового рівня розвитку дитини. Ця робота передбачає організацію розвиваючого навчання, яке на уроках математики повинно забезпечувати математичний розвиток школяра. У багатьох дослідах психологів та педагогів проблема організації розвиваючого навчання дітей будь-якого рівня розвитку пов’язується із спеціальними заняттями. Академік В.В. Давидов в цьому зв’язку наголошував: розвиток дитини в великій мірі залежить від тієї діяльності, яку вона виконує в процесі навчання.

Розглянемо докладніше погляди психологів на це питання.

Один із видатних дослідників розвитку дитячого мислення швейцарець психолог Ж. Піаже стверджував, що формальний інтелект виникає незалежно від шкільного навчання. Здатність оперувати з мисленими замінниками предметів приходить до дитини у свій час, незалежно від того, вчимо ми її чи ні. Вона проходить у своєму розвитку строго визначені стадії від доопераційних структур, через стадію формальних операцій до формального інтелекту. Порядок стадій змінити не можна, це закон розвитку мислення. Другий висновок концепції Паже полягає в тому, що розвиток мислення не залежить не тільки від навчання, а й від конкретно-історичних умов взагалі.

У дослідженнях з перевірки отриманих Піаже висновків взяло участь багато психологів. У результаті цієї роботи було висвітлено дві сторони мислення: розсудок і розум, конкретне і абстрактне, емпіричне і теоретичне мислення. Розсудок має справу з предметом у спокої, а розум - з явищем, що діалектично розвивається. Для розсудку виділення загального - вінець мислення, для розуму - його початок. Розсудок відбиває лише зовнішній бік речей, а розум пізнає їхню внутрішню сутність. Емпіричне мислення, основою якого є розсудок, має на меті класифікацію предметів і явищ. Воно виробляється в процесі порівняння предметів і уявлень про них, що дозволяє виявити в них спільні властивості. Емпіричне мислення спирається на спостереження, відбиває в уяві зовнішні властивості предметів. З емпіричним мисленням пов’язане формування таких логічних умінь як порівняння і узагальнення.

Теоретичне мислення розв’язує задачу відтворення сутності досліджуваного предмету і виникає в результаті аналізу ролі і функції деякого особливого відношення всередині цілісної системи. Теоретичне мислення, що виникає на основі мисленого перетворення предметів, відбиває зв’язки. Воно пов’язане з формуванням таких логічних умінь, як абстрагування і узагальнення.

Багато психологів та педагогів не погоджувались з висновками Піаже. Адже ще Л.С. Виготський говорив про провідну роль навчання в розвитку. Над цією ідеєю працювали П.Я. Гальперін, В.В. Давидов, Д.Б. Ельконін, Л.В. Занков, Г.С. Костюк, Н.О. Менчинська, Л. Обухова та ін. Внаслідок їхніх експериментів було видно, що зміни умов навчання привели до змін в особливостях розумової діяльності дітей. Зокрема, відбулося "розхитування" прийнятого положення, що на молодший шкільний вік припадає друга стадія розвитку мислення - стадія конкретних мислитель них операцій (тобто теоретичне мислення для більшості молодших школярів недоступне). Можливості розвитку теоретичного мислення в молодшому шкільному віці досліджувалися в експерименті, проведеному в 60-х роках під керівництвом В.В. Давидова та Д.Б. Ельконіна. Молодших школярів навчали виділяти узагальнений спосіб дій до формування конкретних знань і умінь. Це привело до зміни якості мислення дітей, діти стали спроможними до теоретичних узагальнень. Приступаючи до розв’язування навчальної задачі, учні аналізували ситуацію, вели пошук загального підходу, істотного відношення. Розвивалася здатність психіки розглядати процес розв’язування задачі з боку, тобто аналізувати власні дії. Учні навчилися планувати власні дії "в умі" до реального їх здійснення. "Феномен Піаже" почали трактувати як такий, що стосується лише емпіричного мислення.

Так, силами багатьох науковців формувалася протягом століття концепція розвивального навчання. Ця концепція була покликана шукати вже в молодшому шкільному віці шляхи розвитку повноцінного мислення, здатного ефективно розв’язувати різноманітні життєві задачі в умовах бурхливого науково-технічного розвитку суспільства. Одним із таких шляхів є позакласна робота з математики.

Але для визначення найбільш ефективних форм цієї роботи важливо більш докладно розглянути особливості розумового розвитку учнів початкових класів. Естонський психолог І.Е. Унт в основу відмінностей між дітьми кладе комплексну властивість - рівень розумового розвитку. Ця властивість охоплює три аспекти:

1) здатність до навчання;

2) набуті знання, навички і вміння;

3) вміння розумової праці.

Здатність до навчання визначається швидкістю засвоєння, гнучкістю процесу мислення та зв’язком конкретних і абстрактних компонентів у мисленні. Істотним показником швидкості засвоєння є не стільки швидкість запам’ятовування, скільки темп узагальнень.

Другим аспектом рівня розумового розвитку учня є наявні у нього на даний момент знання, навички і вміння. Здатність до навчання являє собою потенційні можливості. А знання є змістовною базою для реалізації здібностей. Рівень знань визначається як програмовими так і позапрограмовими знаннями. У будь-якому класі учні відрізняються один від одного саме рівнем знань.

Третім аспектом рівня розумового розвитку є вміння розумової праці. Ці вміння найбільш наочно проявляються в самостійній роботі учнів з навчальним матеріалом: при сприйнятті і обробці нового матеріалу, при виділенні з нього суттєвого, при пов’язуванні нового матеріалу з попереднім, при узагальненні і повторенні, при застосуванні нового матеріалу. При вивченні математики вміння розумової праці мають особливе значення.

Звичайно, тільки окремим дітям притаманні всі ці аспекти вмінь розумової праці. У більшості ж дітей при виконанні певного завдання свідомість спрямовується в основному на усвідомлення сутності завдання. У процесі його розв’язування в кращому випадку контролюється якість проміжних результатів. Власні ж розумові дії при цьому мало усвідомлюються. Свідомість учня, який володіє повноцінним вмінням учитися має двосторонню спрямованість: то на задачу, то на самого себе - на те, як власна психіка (увага, пам'ять, уява, мислення) справляється з цією задачею.

Психолог З.І. Калмикова рівень розумового розвитку і вміння розумової праці розглядає як одне комплексне поняття під назвою "научуваність". Під научуваністю вона розуміє складну динамічну систему інтелектуальних властивостей особистості, якостей розуму, що перебувають у стадії формування, від яких залежить продуктивність навчально-пізнавальної діяльності (при наявності вихідного рівня знань, позитивної мотивації та ін). Серед компонентів научуваності З.І. Калмикова виділяє глибину, гнучкість, стійкість, свідомість і самостійність мислення.

Глибина мислення проявляється у ступені істотності ознак, які людина може абстрагувати при розв’язанні проблем, і в рівні їх узагальнення.

Гнучкість розуму передбачає подолання бар’єру минулого досвіду, вміння відійти від звичних ходів думки, оригінальність розв’язань, їх своєрідність.

Стійкість розуму визначає ту сторону мислительної діяльності, яка дозволяє людині при розв’язуванні проблем утримувати в голові всю сукупність виділених істотних ознак, діяти у відповідності до них, не піддаючись на провокаційний вплив зовнішніх, випадкових ознак.

Свідомість мислительної діяльності означає можливість зробити цю діяльність предметом мислення самого суб’єкта. У близькому значенні вживається термін "рефлексія".

Самостійність мислення проявляється при оперуванні новими знаннями і полягає у вміннях з’ясувати цілі, проблеми, висунути гіпотезу, самостійно розв’язати ці проблеми.

Ми розглянули основні аспекти рівня розумового розвитку - комплексної властивості, яка лежить в основі відмінностей між дітьми стосовно їхньої навчальної діяльності.

Серед спільних особливостей дітей молодшого шкільного віку можна назвати схильність наслідувати, діяти за зразком, а також велику зацікавленість навчальною діяльністю на перших порах навчання в школі, яка може швидко згаснути при неправильній організації навчально-пізнавальної діяльності.

Отже, велике значення у математичному розвитку молодших школярів має пізнавальний інтерес.

Досліджуючи пізнавальний інтерес у дітей молодшого шкільного віку, В.Е. Щепінська умовно виділила чотири рівні його розвитку і свідомого відношення до предмету та оволодіння ним.

Перший рівень - в учня відсутній інтерес до всякої пізнавальної діяльності, йому притаманний вузький розумовий світогляд, навчається лише через бажання уникнути неприємностей, не бажає застосовувати вольові зусилля для подолання труднощів навчальної діяльності, результатом чого є відсутність самостійності у такого учня.

Другий рівень - учень проявляє інтерес до цікавої сторони навчального матеріалу, але ще без бажання проникнути в сутність вивчаючого явища, має вузький розумовий світогляд як результат несформованості пізнавального інтересу, мотиви навчання лежать поза навчальною діяльністю - він навчається для батьків, а не для себе і тому проявляє слабкі вольові зусилля для вивчення математики, самостійність його потребує стимулу й контролю з боку вчителя. Проте вивчивши передовий педагогічний досвід та психолого-педагогічну літературу, В.Е. Щепінська визначила, що у цих учнів повністю можна сформувати свідоме відношення до вивчення математики і інших предметів на більш високих рівнях.

Третій рівень - учень проявляє вже безпосередній інтерес до предмета, проте ще без вміння проникнути в сутність явища, його розумовий світогляд розширюється за рахунок інтересу, що виник, мотиви навчання хоч і лежать поза навчальною діяльністю, проте досягнути більш високого ступеня розвитку - це почуття відповідальності перед колективом, усвідомлення потрібності знань з предмета. Учень прикладає певні вольові зусилля для подолання труднощів в вивченні матеріалу, проте все ж таки його самостійність проявляється лише при наявності інтересу лише до матеріалу, який вивчається на уроці.

Четвертий рівень - в учня появився інтерес до сутності явища, тобто пізнавальний інтерес. Його світогляд розширився до нормального для даного віку рівня, в основі мотивів навчання лежить інтерес до самого предмета. Учень прикладає вольові зусилля для оволодіння матеріалом, методами вивчення предмету, виявляючи при цьому прагнення до повної самостійності як на уроках, так і на позакласних заняттях.

Самі лише уроки з математики не завжди дають простір для розвитку пізнавального інтересу. В зв’язку з цим великого значення набуває позакласна робота.

Отже, можна сказати, що найважливішими особливостями, які лежать в основі індивідуальних відмінностей учнів, є такі: загальні розумові здібності; програмові та позапрограмові знання, навички і уміння; вміння розумової праці; пізнавальні інтереси. Розглянемо у контексті нашої проблеми особливості психічних процесів молодших школярів.

Щодо пам'яті, то у молодших школярів мимовільна пам'ять розвинута краще, ніж довільна, наочно-образна пам'ять переважає словесно-логічну. Як показали дослідження Л.В. Занкова, розвитку логічної пам'яті сприяє виконання учнями таких завдань, у яких треба виділяти і розуміти головне. Одним із стимулів розвитку логічної пам'яті та логічного мислення є позакласна робота з математики.

У молодшому шкільному віці мимовільна уява переважає довільну; недостатньо розвинута репродуктивна і творча уява. Це дає свій відбиток і на розвиток мислення - в цьому віці і конкретне, і тим більше абстрактне мислення перебувають на початковій стадії розвитку. Щодо темпів розумового розвитку в молодшому шкільному віці, то вони мають ту особливість, що найбільше зрушення в розвитку дитини відбувається на перших періодах навчання, а далі у багатьох дітей темпи розумового росту дещо сповільнюються. У нашій експериментальній роботі, аналізуючи зрушення, які відбудуться у розумовому розвитку молодших школярів внаслідок проведення позакласної роботи з математики, ми будемо вивчати всі три аспекти розумового розвитку учнів. Адже позакласна робота з математики у початкових класах у значній мірі і виховує здатність до навчання, і визначає рівень знань, і формує й закріплює навички та вміння, і виховує вміння розумової праці у школярів, і розвиває інтерес до математики.

Отже, з проведеного аналізу психолого-педагогічних особливостей молодших школярів можна зробити такий висновок. Поряд з уроками кожен вчитель повинен використовувати позакласну роботу з математики як для сильних, так і для слабких та середніх учнів. Адже вона сприяє глибокому і міцному оволодінню матеріалом, підвищенню математичної культури, виробленню навичок самостійної роботи, розвиває мислення, здатність здійснювати розумові операції, закріплює і не дає втратити дитині інтерес до вивчення математики, розвиває творчі здібності дитини. Тому позакласна робота з математики у початкових класах є невід’ємною складовою навчально-виховного процесу і повинна займати вагоме місце у педагогічній роботі кожного вчителя початкових класів.

1.2 Види позакласних занять з математики

Позакласна робота сприяє поглибленню знань, яких набувають учні на уроках, прищепленню навичок застосовувати ці знання на практиці, вихованню моральних якостей: волі, наполегливості, критичного ставлення до виконаної роботи, а також розвиває інтерес до вивчення предмету.

Форми організації позакласної роботи і методи проведення її відрізняються від форм і методів проведення навчальних занять у школі. Час, кількість і види позакласних занять визначаються їх характером, метою і віком учнів.

Є такі форми проведення позакласної роботи з математики в початкових класах:

Олімпіада.

Математичний гурток.

Математичний ранок.

Хвилини цікавої математики.

Години цікавої математики.

Випуск математичних газет.

Математичні екскурсії.

Створення математичного куточка.

Олімпіада, як один з видів математичних змагань, має широку популярність у нашій країні. Математична олімпіада у початковій школі - засіб виховання сумлінного ставлення дітей до навчання; одна з форм позакласної роботи, яка створює умови для вияву спортивного азарту, посилює зв’язки сім’ї та школи. Цей вид позакласної роботи цікавий для дітей тим, що тут вони можуть випробувати свої знання, позмагатися з іншими учнями з того чи іншого предмету, і, звичайно, отримати оцінку своїх знань.

Математичні олімпіади молодших школярів мають пропедевтичний характер. Основними рівнями математичних олімпіад учнів початкової школи є класні та шкільні. Міжшкільні й районні олімпіади проводяться за умов належної підготовки працівників районних відділів народної освіти чи методичних кабінетів.

Наступною формою є математичний гурток. Цей вид позакласної роботи у початкових класах допомагає розширенню світогляду учнів у різних областях елементарної математики. Гурткова робота сприяє розвитку у дітей математичного мислення, лаконічності мови, вмілому використанню символіки, правильному застосуванню математичної термінології, умінню робити доступні висновки й узагальнення, обґрунтовувати свої думки та ін. Робота гуртка впливає на підвищення інтересу до математики не тільки гуртківців, але й решти учнів класу. На заняттях гуртка учні можуть реалізувати свої побажання щодо змісту матеріалу, що їх цікавить, форми організації своєї роботи, що і притягує дітей до відвідування цього позакласного навчання.

Ще однією формою позакласної роботи є математичний ранок. Це свято, основу якого складають командні і парні змагання на математичному матеріалі даного класу. Новий і позапрограмовий матеріал має бути, але у невеликому обсязі і в цікавій формі. Математичний ранок потребує ґрунтовного підходу. Ще під час уроків учитель має опрацювати основні форми змагань та ігор, які використовуватимуться на цьому святі. Потрібні репетиції у позаурочний час.

Хвилини цікавої математики - це досить дієвий та ефективний засіб масового охоплення учнів позакласною роботою та розвитку в них інтересу до предмета. Вони проводяться епізодично і є складовою частиною різних видів дозвілля - у групі продовженого дня, під час екскурсій тощо. Їх тривалість 10-20 хвилин. Завдання, що пропонуються у "хвилинах", повинні відрізнятися від тих, що розглядаються на уроках. У переважній більшості вони розв’язуються усно, цікаві за формою і доступні всім.

До групових позакласних занять, метою яких є підвищення інтересу дітей до математики, відносяться години цікавої математики. Молодші школярі знаходяться у такому віці, коли їх цікавість до того чи іншого навчального предмета ще не визначилась, а лише формується. Тому до проведення годин цікавої математики корисно залучати всіх учнів класу. Завдяки цій формі позакласної роботи виховується пізнавальний інтерес у дітей, заохочення до глибшого і конкретнішого вивчення того чи іншого предмету. Години цікавої математики від математичного гуртка відрізняються тим, що гурток створюється за принципом добровільності, з врахуванням дитячих нахилів, можливостей та інтересів, а години цікавої математики проводяться з усіма учнями класу. Члени гуртка, на відміну від учнів, що беруть участь у годинах цікавої математики, періодично влаштовують виставки, на яких демонструють наочні посібники, математичні газети, збірники задач, які складені членами гуртка. І, зрештою, години цікавої математики починають проводити з 1-ого класу, а заняття гуртка лише з 2-ого.

Займаються діти і таким видом позакласної роботи, як випуск математичних газет. Їх корисно випускати в усіх класах початкової школи. У першому класі газету доцільно випускати у 2-му півріччі, коли діти вже освоїлись у школі, вміють читати. На перших порах газету випускає сам учитель або старшокласники під його керівництвом. У 2-4 класах до цієї роботи треба поступово залучати учнів. Математичні газети корисні не лише для учнів, що їх випускають, але й для учнів, які їх читають. Адже з газет можна дізнатися багато цікавої інформації, що не розглядається на уроках. Цей вид позакласної роботи також викликає інтерес до предмету, зацікавлює й притягує учнів до його вивчення.

Однією з цікавих і важливих форм позакласної роботи є математичні екскурсії.

На екскурсіях учні дістають початкові відомості з геометрії, розвивають окомір, а також набувають навичок практично застосовувати математичні знання.

Під час екскурсії можна зібрати числові дані для складання задач на місцевому матеріалі, різних таблиць, діаграм, які потім використовуватимуться на уроках і заняттях математичного гуртка. Отже, цей вид позакласної роботи не лише цікавий дітям, але й корисний для самого вчителя. Адже легше проводити уроки, використовуючи матеріал, який діти самі ж зібрали під час екскурсії.

Математичний куточок у початковій школі можна створити у кожному класі. До його організації слід залучити дітей. Вони повинні виготовити під керівництвом учителя всі наочні посібники. Для цього слід використати гурткові заняття, підготовку до проведення загальношкільних заходів, математичні екскурсії тощо. Цей вид позакласної роботи корисний тим, що діти в будь-який момент можуть звернутися до цього куточка за допомогою. Тут вони можуть знайти і підказку, і цікаве завдання, і захоплюючі відомості.

Так, цікаві задачі, які самостійно склали учні на зібраному під час екскурсії матеріалі, вони виконують на креслярському або іншому цупкому папері і зазначають клас, дату виконання роботи і прізвище виконавців і зберігають у математичному куточку. Там також зберігають цікаві історичні задачі, що відповідають вікові і рівню знань учнів. У куточку повинні бути прилади для креслення діаграм, планів та виготовлення наочного приладдя, а також зразки одиниць мір - одиниці довжини (1 см, 1 дм, 1 м), одиниці площі (1 кв. см, 1 кв. м), одиниці об’єму (1 куб. см, 1 куб. дм, 1 л, 1,5 л), одиниці ваги (1 кг, 500 г, 200г, 100 г, 10 г, 5 г, 2 г, 1г). Тут можуть бути виставки зошитів з математики, альбом вирізок з газет з цифровими даними для складання задач, збірки самостійно складених задач, математичні газети. Також висить тут кольорово оформлена таблиця із завданнями для розв’язування задач, прикладів і різних вправ. Це дає можливість учням між позакласними заняттями діставати нові завдання і виконувати їх. Назва таблиці повинна бути привабливою, наприклад: "Міркуй, розв’язуй, відгадуй!". Таблиця містить список учнів, завдань за тиждень і конверт для відповідей. Через певний час учитель перевіряє розв’язання задач, оцінює роботу балами і результати записує до таблиці. Помилки аналізуються або на позакласному занятті, або після уроків. Містить куточок і таку рубрику, як "Чи знаєте ви?", що може включати такі відомості:

… Найбільшими гризунами, які живуть у нашій країні, є бобри. Довжина їх тіла досягає 1 метра, а маса - 30 кілограмів.

… Висота жирафа досягає 5-6 метрів.

… Тривалість життя вовка - 15 років, кролика - 12, зайця - 7 років.

Отже, існує багато видів позакласної роботи з математики в початкових класах. Кожен із них відіграє важливу роль у всій позакласній роботі, містить в собі певні навчальні й виховні моменти. Тому вчителі повинні враховувати всі форми цієї дуже важливої роботи під час навчання, виховання й всебічного, гармонійного розвитку дітей.

1.3 Стан досліджуваної проблеми в теорії і практиці навчання математики

Проблема організації позакласної роботи і її роль в математичному розвитку школярів вже досить довгий час розв’язується науковцями, психологами, педагогами й самими вчителями початкових класів.

Насамперед дослідників цікавить те, як впливає позакласна робота з математики у початкових класах на розумовий розвиток дітей, розвиток їх пізнавального інтересу, всебічний розвиток та формування особистості загалом.

У широкому спектрі досліджувану проблему вивчали М.В. Богданович, Є.П. Морокішко, В.І. Чепелєв, Н.Д. Моцик, Л.С. Іванова, Б. Друзь, Л.М. Дудко, В.П. Руднєв та ін.

Роль математичних олімпіад у позакласній роботі з математики в початковій школі вивчали О.В. Усенко, Я.В. Корнішевський, М.В. Богданович, О. Царінна, Д.В. Клименченко, О. Дюдіна, Л.Ф. Пікуль та ін.

Роль та види математичних гуртків розглядали О.І. Мінхаірова, Е.Т. Розумовська, Т. Вітанов, З.І. Мойсеєва, В.І. Єфімова, Е.А. Дишинський.

Проведення й значення математичних ранків вивчали М.В. Богданович, Т. Хайруліна, В. Шпакова та ін. Щодо проведення математичних екскурсій можна назвати таких науковців як Н.І. Багрій, З.М. Литовченко, Є.П. Морокішко та ін.

Указані дослідження висвітлені, на даний час, в різних методичних посібниках та журналах. Вчителі використовують їх у своїй роботі. Розроблено багато методичних рекомендацій для проведення позакласної роботи з математики. Існує багато посібників з запропонованими завданнями й теоретичним матеріалом для цієї роботи у школі. Проте, цілісної системи позакласних заходів з математики для початкових класів на сьогодні не існує. Все залежить від вибору вчителя.

Щодо використання позакласної роботи з математики вчителями початкових класів на практиці, можна сказати, що вона ведеться, на жаль, не завжди так, як би повинна. Вчителі завжди розуміли значення позакласної роботи для розвитку дитини. Вони завжди придумували і використовували нестандартні, позапрограмові завдання і форми роботи з дітьми. Майстерність класоводів зростала із запровадженням нової освіти для вчителів початкових класів, а також із створенням сітки інститутів удосконалення учителів.

Ми можемо спостерігати розроблені й обґрунтовані ті чи інші види позакласної роботи з математики в початкових класах.

Так, М.В. Богданович та О. Царінна запропонували розробку олімпіад для 2, 3, 4 класів (додаток 2). Вони пропонують систему задач для класної олімпіади, яка визначається 6 задачами для кожного класу, всього 18. Між задачами для різних класів, які йдуть за одним і тим же номером, є деяка подібність.

Перша задача у кожному класі присвячена принципам письмової нумерації натуральних чисел у десятковій системі числення.

Другі задачі пов’язанні з поняттям арифметичних дій, алгоритмами їх виконання чи правилами порядку виконання.

Треті задачі - це майже звичайні (програмові) для даного класу задачі, але вони містять деяку обставину, яка утрудняє процес розв’язування.

Четверті задачі - програмові для даного класу, зокрема, так звані типові задачі. Особливість їх виявляється в дещо ускладненій сюжетній ситуації.

П’яті задачі - майже всі не програмові для даного класу. Здебільшого це типові задачі, але дібрані за принципом випереджуючого навчання.

Шості - геометричного змісту. Це задачі на поділ і складання многокутників; задачі, пов’язані з периметром чи площею прямокутника.

Резервна задача 2 класу - це так звана логічна задача, яка розв’язується способом послідовного вилучення; у 3 класі резервними є задачі „на переливання" чи „зважування"; у 4 класі - задачі з комбінаторики (на обчислення числа комбінацій, розміщення, перестановок).

За сюжетом задачі наближені до діяльності самих учнів та їхніх інтересів, до реальних подій навколишнього життя. Є цікаві задачі, задачі з казковим чи історичним сюжетом, задачі з ігровими ситуаціями.

Саме такими, на думку дослідників, повинні бути класні олімпіади для досягнення поставленої мети.

Автори, провівши математичну олімпіаду у 1 класі, підтверджують доцільність такої форми роботи. Олімпіади подобаються, зацікавлюють і дітей, і батьків. Вчителю допомагають намітити, які завдання варто опрацювати на уроці додатково, і якими новими, оригінальними методами можна розв’язати задачу чи приклад. Цей вид математичних змагань сприяє розвитку не лише математичних здібностей, а й самостійності, впевненості, старанності учнів. Його варто починати практикувати з 1-ого класу, стверджують М.В. Богданович та О. Царінна.

Д.В. Клименченко у своєму досвіді запевняє, що твердження деяких науковців про те, що різноманітні види позакласної роботи потрібно проводити лише в старших класах, є безпідставним. Він з своїх досліджень наводить приклад, що діти 7-9-річного віку охоче займаються математикою в позаурочний час. Зупиняється він на математичній олімпіаді. Також свою версію математичних олімпіад в початковій школі запропонувала Олена Дюдіна. Вона свою систему завдань пропонує для 2-ого класу. Спершу діти проходять три відбіркових тури на класному рівні змагань. Переможці беруть участь у шкільній олімпіаді, що теж пропонується Оленою Дюдіною. А далі їх чекає міська олімпіада, рівень складності завдань якої набагато вищий за шкільну. Її зміст добирається таким чином, що, з одного боку, не виходить за рамки програми, а з другого - дає можливість учням спробувати свої сили у нестандартних завданнях підвищеної складності. Завдання для міської олімпіади пропонуються з посібника „Цікаві задачі логічного характеру”, складеного доцентом КДПУ ім.В. Винниченка Т.О. Фадєєвою. Ці завдання розділені на певні групи: задачі, пов’язані з віком та родинними стосунками; задачі, що мають логічну та обчислювальну частину; задачі, основою яких є нумерація багатоцифрових чисел; задачі на арифметичні дії та зв’язок між ними. Найдоцільніші з цих задач також пропонуються дослідницею.

Цікавим є досвід Л.Ф. Пікуль, що пропонує перед математичною олімпіадою перевірку готовності дітей до неї (Додаток 3). Так, її олімпіада проводиться на зимових канікулах, в гарно оформленому приміщенні. Тобто для дітей - це не лише змагання в розв’язуванні завдань, а й свято, де є ведуча - Королева Математики, що спершу пропонує їм розв’язати 3 завдання, мовляв, перевірити їхню готовність до олімпіади. А далі проводить звичайну олімпіаду.

Також ми маємо змогу ознайомитися із досвідом зарубіжних науковців. Так, нам пропонує свої заняття математичного гуртка Т. Вітанов з Болгарії. Ним та іншими дослідниками створений посібник „На допомогу керівнику математичного гуртка в 4-му класі середньої школи". Ця книжка складається з трьох розділів: арифметики, геометричного світу та математичної мозаїки.

Розділ „Арифметика", в свою чергу, складається з 6-ти параграфів: „Використання властивостей арифметичних операцій та розвиток навичок усної лічби"; „Виникнення чисел"; „Системи числення й різноманітні записи чисел"; „Задачі з дробами, проценти і діаграми"; „Текстові задачі"; „Подільність чисел"; „Рівність в цілих числах".

В розділі „Геометричний світ” лише дві теми: „Симетрія фігур та орнаменти”; „Прямокутний паралелепіпед, його об’єм та площа поверхні".

„Математична мозаїка" складається з 5-ти основних параграфів. Основні теми такі: „Логічні задачі”; „Елементи теорії графів”; „Принцип Діріхле"; „Числові ребуси”. Вибір тем в посібнику не є випадковим - він відповідає шкільній гуртковій програмі.

Михайло Богданович, Тетяна Хайруліна та Валентина Шпакова пропонують нам один із розроблених ними сценаріїв математичного ранку, що є невід’ємною частиною позакласної роботи в початкових класах (Додаток 4).

Дуже цікавим є досвід проведення математичних екскурсій Н.І. Багрія та З.М. Литовченко (Додаток 5), а також запропонований нам М.А. Циварєвою метод проектів в позакласній роботі з математики. Вона помічає, що в сучасній педагогічній літературі рекомендується використовувати проективну діяльність переважно у навчанні підлітків. Це обумовлено, перш за все тим, що при розробці проекту від учнів потрібна велика самостійність, вміння працювати з різними джерелами інформації, здібність до навчання й взаємодії, які в учнів початкових класів ще не сформовані. Але в той же час під керівництвом вчителя в процесі позакласної роботи молодші школярі поступово зможуть оволодіти необхідними якостями та вміннями, запевняє М.А. Циварьова. І тому пропонує нам можливості використання методу проектів при вивченні теми „Час та його вимірювання”.

Існує багато посібників які містять як зразки різних видів позакласної роботи з математики для початкових класів, так і методичні рекомендації щодо їх проведення. Так, можна назвати методичний посібник „Позакласна робота з математики у початкових класах”, складений Н.Д. Моциком та Л.С. Івановою, а також посібник „Позакласна робота з арифметики”, розроблений та складений Є.П. Морокішко та В.І. Чепелєвим. Також видані посібники з матеріалом для проведення позакласної роботи. Наприклад, посібник „Цікава математика” О.П. Корчевської та „Математична мозаїка" Б. Друзя.

Це є великим здобутком для вчителів початкових класів. Адже їм пропонується і методика проведення, і зразки різноманітних видів позакласної роботи. І хоч немає цілісної системи позакласних заходів, та вчитель повинен сам складати план своєї позакласної роботи. Адже це досить індивідуальна й зовсім не універсальна робота. Підбір позакласних заходів залежить від інтересів й рівня сформованості розумового розвитку дітей, від знань, умінь та навичок, які потрібно сформувати в учнів. Проте не всі вчителі використовують позакласну роботу у навчанні й вихованні. Більшість відговорюються тим, що діти й так завантаженні навчальним матеріалом, що їм вистачає й цього. Але в результаті отримують лише величезне небажання зі сторони учнів до навчання й відсутність будь-якого пізнавального інтересу і, як результат, - низький рівень навчання. Адже саме завдяки різним формам позакласної роботи можна досягти зацікавленості дітей тим чи іншим предметом, розвинути бажання займатися дослідженням позапрограмового матеріалу, насамперед, викликати пізнавальний інтерес у дитини і в підсумку отримати позитивні результати навчання учнів.

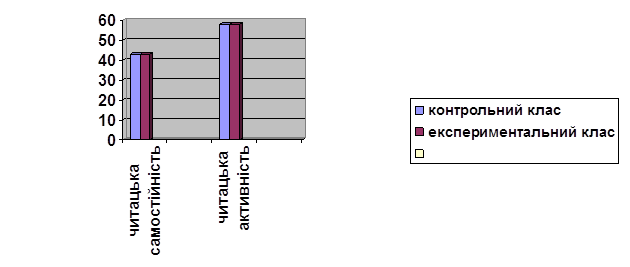
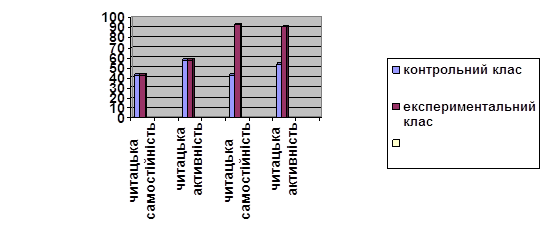
Що стосується роботи тернопільських вчителів, я провела анкетування у Тернопільській загальноосвітній школі №23, де проходила практику. Завдяки цьому анкетуванню я мала на меті з’ясувати стан проведення позакласної роботи з математики. Мене цікавили такі питання: чи використовують вчителі позакласну роботу з математики у своїй діяльності; які форми позакласної роботи з математики переважають у їх діяльності; у якому класі розпочинають позакласну роботу з математики; як часто використовують позакласну роботу; чи проводили самі дослідження ефективності цієї роботи; які способи та методи позакласної роботи найдоцільніші й найефективніші; з якими учнями переважно проводять позакласну роботу з математики; на розвиток якої якості потрібно робити акцент під час проведення позакласної роботи з математики; чи оцінюють учнів під час позакласної роботи.

Анкетуванням було охоплено 15 вчителів. Результати анкетування показали, що фактично всі вчителі початкових класів в тій чи іншій мірі проводять позакласну роботу з математики. Проте, я помітила, що цілеспрямовано, з проведенням підготовки, самостійною роботою учнів у позакласний час, з використанням змістовних, планових, масових видів позакласної роботи у повсякденній практиці працює досить незначна кількість учителів. Основна маса орієнтується на програму, а позакласну роботу використовує епізодично і безсистемно. Спостерігаючи за роботою вчителів та спілкуючись з ними безпосередньо, я виявила, що стаж і педагогічний досвід не є основною причиною відмінностей між учителями. Я дізналась, що багато з них ігнорують позакласну роботу через брак часу, через велику кількість слабких учнів у класі, через небажання дітей, через низьку заробітну плату.

Отже, проведений аналіз засвідчує, що позакласна робота з математики у початкових класах не повністю ведеться не через те, що немає методичних вказівок й зразків її проведення, а через те, що деякі вчителі не мають бажання її проводити з певних причин. Про це дуже сумно дізнаватися, адже робота такого вчителя вже не має потрібної ефективності, не зацікавлює дітей, а навпаки відбиває в них бажання вчитися. Звісно, таке навчання не призведе до повного всебічного розвитку молодої особистості.

Я вважаю, що кожен вчитель, який хоче справді навчити й виховати дітей, повинен віддаватись своїй роботі на 100%. Тобто, використовувати всі можливі форми і види роботи, у тому числі і позакласну роботу. Але, на жаль, проконтролювати проведення позакласної роботи неможливо, адже це лише справа вчителя та дітей.

Розділ 2. Методика організації позакласної роботи з математики в початкових класах 2.1 Особливості методики позакласної роботи з математики в початкових класах

Основні завдання позакласної роботи такі: поглиблювати і розширювати знання та практичні навички учнів; розвивати логічне мислення, кмітливість, математичну пильність, виявляти найбільш обдарованих і здібних дітей, сприяти їхньому дальшому розвитку, виховувати інтерес до математики; залучати дітей до цікавих занять; виховувати наполегливість, любов до праці, організованість і колективізм.

Учитель повинен детально продумувати організацію позакласної роботи з тим, щоб вона забезпечувала активність, ініціативу і самостійність учнів. Він може використовувати такі види позакласної роботи з математики як:

математичні олімпіади;

математичний гурток;

математичний ранок;

хвилини цікавої математики;

години цікавої математики;

математичні екскурсії;

випуск математичної газети;

створення математичного куточка.

Організація і проведення позакласної роботи з математики в початкових класах мають свої особливості:

розпочинаємо позакласну роботу з математики з хвилинок цікавої математики у ІІ півріччі 1-ого класу;

основними формами роботи на позакласних заняттях з математики є ігрова та практична діяльність учнів - використання дидактичних ігор; створення проблемних ситуацій, розв’язування задач-віршів, задачок - казочок; відгадування загадок, ребусів тощо;

наочність на заняттях повинна бути яскравою, привабливою, цікавою для дітей.

Позакласну роботу будують за принципом добровільності. Тут учням не виставляють оцінок, однак обґрунтованість суджень, кмітливість, швидкість обчислень, використання раціональних способів розв’язування треба заохочувати. Для позакласної роботи добирається доступний матеріал підвищеної складності або такий, що доповнює вивчення основного курсу математики, але з урахуванням наступності з класною роботою.

Своєрідно проводиться облік участі учнів у цій роботі і результатів її виконання. Певним звітом з позакласної роботи є олімпіади, математичні вечори, конкурси, спеціальні газети, альбоми та ін.

Учителю належить керівна роль у проведенні позакласної роботи, але це керівництво тут має певну специфіку. Учитель допомагає учням планувати позакласні заняття, підбирати необхідний матеріал і посібники, проводити окремі заходи, даючи їм можливість проявити власну ініціативу на всіх етапах підготовки і проведення занять.

Позакласні заняття дають широкий простір для самостійної роботи учнів, розвитку їх ініціативи, самодіяльності, виявлення творчих здібностей. Вони також допомагають у розвитку уваги і спостережливості, що є важливою умовою успішного навчання.

Розпочинають цю роботу вже з першого класу з проведення хвилинок цікавої математики. На цих заняттях учні граються в різноманітні ігри, які вже з перших днів перебування в школі вчать їх бути уважними і спостережливими, вимагають від них уваги і вміння спостерігати зміни в навколишньому середовищі.

Вже у другому класі добрим засобом для розвитку уваги дітей є усна лічба, яку бажано практикувати на кожному позакласному занятті. Вона також виховує у дітей почуття відповідальності за виконану працю. Особливо цьому сприяють позакласні заняття, на яких проводяться змагання за точні результати лічби. Наприклад, у класі проводять математичну естафету. Підсумовуючи результати роботи, легко побачити, хто неуважно лічив і яку допустив помилку. Між учнями виникає творче змагання за кращі результати лічби, вони здійснюють при цьому самоконтроль, вчаться перевіряти себе, свою роботу і знаходити в ній помилки та виправляти їх. А ці навички дуже корисні, і їх треба прищеплювати дитині.

Вже у третьому класі використовують розв’язування цікавих задач, задач-жартів і головоломок, що сприяє розвитку логічного мислення, кмітливості, мови учнів.

Також на позакласних заняттях формується уявлення у дітей про геометричні фігури. Дітей навчають будувати прямі кути, прямокутники, квадрати, вимірювати недоступні висоти, відстані, площі тощо. Для виконання практичних робіт потрібні прилади: екер, віхи, транспортир, польовий циркуль та ін. Усі ці прилади можна виготовити з учнями після уроків у шкільній майстерні, під час занять математичного гуртка, або індивідуальної позакласної роботи учнів.

Розглянемо методичні особливості організації та проведення окремих видів позакласної роботи з математики в початкових класах.

Хвилини цікавої математики.

Вся позакласна робота розпочинається з проведення хвилин цікавої математики. Вони проводяться з метою розвитку в учнів вже першого класу інтересу до предмету математики.

Компонувати матеріал для хвилин цікавої математики можна по-різному. Один раз запропонувати ребуси, другий головоломки, третій - задачі-жарти. Але, як показує практика, доцільно комбінувати різні види завдань. Ці завдання можуть бути присвячені певній темі, наприклад, закріпленню геометричного матеріалу, таблиць множення, розв’язуванню віршованих задач на дві дії тощо.

Години цікавої математики.

Щодо годин цікавої математики, то кожне заняття вчитель планує відповідно до вимог щодо підвищення інтересу дітей до математики та з урахуванням знань, умінь і навичок, які мають учні на час проведення цієї роботи. Проведення групових занять з цікавої математики бажано розпочинати з другого семестру першого класу. Тривалість таких занять може бути у першому класі - 15-20 хвилин, у другому - 20-25 хвилин, у третьому-четвертому класах - 30-35 хвилин.

Години цікавої математики у першому класі проводяться епізодично, а в других-четвертих їх бажано проводити систематично один-два рази на місяць.

Матеріал до занять підбирається різноманітний, але всі завдання мають бути цікавими як за змістом, так і формою їх проведення. Години цікавої математики можуть бути тематичними - всі завдання на занятті присвячені одній темі програми: "Таблиці додавання і віднімання у межах 10", "Прості задачі", "Таблиця множення" та інші. Проте найчастіше проводяться комбіновані заняття, до яких включається цікавий матеріал з різних тем програми.

Кожна година цікавої математики може складатися з трьох частин: вступної, основної і заключної. У вступній частині діти повинні відразу відчути незвичність заняття, його відмінність від уроку. Пропонуємо учням ребуси, задачі у віршах або розпочинаємо заняття від імені казкових героїв, які пропонують дітям цікаві завдання. В основну частину включаємо завдання, які вимагають більш напруженої розумової діяльності учнів. Це завдання з логічним навантаженням, різноманітні задачі підвищеної складності, задачі-загадки, задачі-жарти. До заключної частини включаємо математичні чи логічні ігри, загадки. Корисно закінчувати заняття на найцікавішому етапі, коли діти захоплені грою, це буде для них "зарядом цікавості" на наступне заняття.

Математичний гурток.

Для глибшої роботи з дітьми з предмету, починаючи з 2-3 класу, організовують математичні гуртки.

Гурток створюється за принципом добровільності. При наборі дітей до гуртка треба враховувати їхні нахили, можливості та інтереси. Не обов’язково, щоб членами гуртка були лише здібні і підготовлені учні. Треба прагнути викликати зацікавленість до гурткової роботи і з боку середніх та слабких учнів. Стимулом до організації математичного гуртка може стати спеціально проведена коротка бесіда вчителя про те, чим діти будуть займатись у цьому гуртку. Таку бесіду можна провести на уроці у зв’язку з вивченням тієї чи іншої теми, при розв’язуванні задач та ін.

У залежності від умов гурток можна створити або загальношкільний для учнів паралельних класів, або окремий для учнів одного класу.

Заняття математичного гуртка доцільно проводити не частіше 1-2 разів у місяць, оскільки кожне заняття вимагає детальної підготовки як з боку вчителя, так і учнів.

Методи проведення занять гуртка більш різноманітні, ніж інших занять. Це зокрема: короткі повідомлення членів гуртка чи вчителя з історії розвитку математики; вправи на розв’язування цікавих задач, ребусів, загадок, задач підвищеної складності; розв’язування логічних вправ; виготовлення наочних посібників; випуск газет; дидактичні ігри та ін.

Всі матеріали - результати роботи гуртка - повинні зберігатися у класі.

Члени гуртка періодично влаштовують виставки, на яких демонструють наочні посібники, математичні газети, збірники задач, які складені членами гуртка за числовими даними, що взяті з життя, матеріали цікавих повідомлень, екскурсій і т.д.

Підбиваючи підсумки роботи математичного гуртка, вчитель можне додати ще кілька математичних ігор, які можна використати як у позакласній роботі з учнями І-ІІ класів, так і на уроках. Разом з тим, вона є джерелом знань учнів на ранніх стадіях математичної освіти. Вибирати ігри треба відповідно до віку дітей, змісту матеріалу уроку і рівня знань учнів.

Математичні газети.

Математичні газети випускаються з метою зацікавити позакласною роботою й інших учнів, продемонструвати усім результати роботи тих, хто займається у математичних гуртках та інших формах цієї роботи.

У зв’язку з тим, що в класі можуть випускатись газети з різних предметів, математична газета може оформлятись двічі-тричі на півріччя.

Математична газета у 1-2 класах повинна стати дійовим помічником учителя у прищепленні дітям інтересу і любові до математики, у вихованні кмітливості, логічного мислення. Вона повинна бути агітатором математичного гуртка, висвітлювати матеріали і результати математичних конкурсів, вікторин. У ній варто розміщувати цікаві задачі-головоломки, задачі-жарти, логічні вправи у формі запитань, загадок, задач у віршах.

Оформлення математичної газети відіграє важливу роль. Яскраво ілюстрована, гарно написана газета притягує увагу дітей. Неабияке значення має назва газети. В її виборі діти повинні взяти активну участь. Це може бути "Чомучка", "Плюсик", "Математична веселка", "Юний математик" та ін.

Математичний куточок.

Математичний куточок створюється з метою заохочення дітей до збору цікавих матеріалів, складання своїх завдань для однокласників.

Від математичної газети він відрізняється тим, що висить у класі весь час і не створюється кожен раз наново, а містить окремі відділення, вміст яких весь час змінюється, поповняється самими дітьми.

Отже, в організації математичного куточка також беруть участь самі діти. Збирання числового матеріалу для його заповнення треба організувати так, щоб діти самостійно брали із життя, газет і журналів або при вивчені інших дисциплін цікаві для них числові дані. З метою заохочування учнів до цього слід відмічати тих, хто найчастіше поповнює куточок новими числовими даними. Можна використовувати матеріал математичного куточка на уроках, вказуючи при цьому, хто його надав.

Математичні екскурсії.

Досить рідкісною та не менш ефективною формою позакласної роботи є математичні екскурсії. Вони використовуються для застосування учнями своїх знань на практиці, отимання нових знань, збору інформації й використання її пізніше на заняттях, в оформленні математичних газет та поповненні математичного куточка.

Кожній екскурсії повинна передувати старанна підготовча робота. Учителю слід спочатку визначити мету екскурсії і, виходячи з цього, обрати для неї об’єкт. Потім він повинен оглянути місцевість або об’єкт, на який передбачено повести учнів, скласти план екскурсії. Якщо метою екскурсії є проведення вимірювальних робіт на місцевості, то вчителю слід спочатк виконати всі роботи самому з допомогою трьох-п’яти активістів математичного гуртка.

Після цього треба провести бесіду з учнями, щоб з’ясувати мету екскурсії та завдання гуртківців у підготовці до неї (виготовлення необхідних приладів тощо). Якщо, наприклад, метою екскурсії є вимірювання відстані на око, кроками, мірним шнуром і рулеткою, то треба під час бесіди запропонувати виготовити мірний шнур, віхи. Крім того, кожний учасник екскурсії повинен знати довжину власного кроку. Вчитель дає дітям поради, як саме її визначити. Слід також за годинником визначити, яку відстань проходить учень за певний час. Ці дані можна використати при вимірювані кроками великих відстаней.

Якщо діти ніколи не вправлялися у вимірюванні відстаней на око, то бажано спочатку на занятті математичного гуртка провести окомірне вимірювання невеликих розмірів (довжина і ширина зошита, довжина класної дошки, парти, довжина і ширина класу та ін).

Слід розробити форму запису даних, одержаних під час екскурсій, ознайомити з нею учнів і запропонувати їм заздалегідь підготувати цю форму.

Кожна екскурсія повинна закінчуватись заключною бесідою, в якій підсумовують роботу, відзначають кращих учнів, що успішно виконали завдання. Матеріал екскурсії після відповідного оформлення вміщують у математичному куточку. Теми екскурсій можуть бути і такі: "Ціна, кількість, вартість." - екскурсія в магазин, "Відстань" - екскурсія по дорозі, коли діти, щоб краще уявляти міри довжини, проходять самі метр, кілометр, "Швидкість" - де діти, за допомогою вчителя визначають свою швидкість та ін.

Математичні олімпіади.

Цей вид позакласної роботи проводиться з метою заохочення учнів до предмету шляхом змагання, які так цікавлять дітей молодших класів, перевірити їх знання, порівнюючи з іншими.

Істотною особливістю математичних олімпіад молодших школярів і необхідною умовою їх ефективності є масовість. Кожному учню повинна бути надана можливість взяти у ній участь. Реальним заходом забезпечення масовості є організація і проведення класних олімпіад.

Другою особливістю і другою необхідною умовою ефективності олімпіад молодших школярів є опосередкована та безпосередня участь батьків у їх підготовці. Реально цього можна досягти, якщо протягом певного часу учням у порядку підготовки пропонувати розв’язувати вдома деяку кількість "нестандартних " задач. Зрозуміло, що процес опрацювання нестандартних задач буде включати консультації і допомогу батьків чи старших братів і сестер.

Третьою особливістю і важливою умовою здійснення математичних олімпіад молодших школярів є повне забезпечення вчителя "задачним матеріалом" як до змісту завдань самої роботи олімпіади, так і до завдань підготовчої роботи.

Четвертою особливістю і необхідною вимогою є проведення олімпіади в умовах заохочувального режиму. Кожен учасник має виступити успішно, тобто розв’язати хоча б одну задачу. Більшість учнів має впоратися з двома-трьома задачами. Переможцями треба вважати третину школярів, яка має кращі результати у розв’язанні задач олімпіади. Виконання усіх завдань не є вимогою для переможців. Усім учасникам олімпіади оголошується подяка і даруються листівки з відповідними записами.

П’ятою особливістю можна вважати поступовість у нарощуванні турів олімпіад. У 2 і у 1 класі проводяться тільки класні олімпіади. У 3 проводяться класні і шкільні, а у 4 - класні, шкільні і міжшкільні (районні).

Всі класні олімпіади бажано провести 5-15 квітня, шкільні - 16-25 квітня. Якщо олімпіада буде продовжуватись і на міжміському рівні, то її можна провести 5-15 травня.

Підготовка до класних олімпіад здійснюється шляхом епізодичного розв’язування нестандартних задач учнями на уроках математики та вдома. Основний період підготовки - березень (три основні навчальні тижні третьої чверті). Підготовкою до шкільних олімпіад є аналіз результатів класних олімпіад та розв’язування відповідних задач. Отже, березень та квітень можна буде назвати місяцями "посиленої математики".

Класні олімпіади проводяться на одному з уроків математики або у позаурочний час, тобто на п’ятому уроці (після відпочинку учнів 15-20 хвилин). Класні олімпіади проводяться за двома варіантами. Задачі олімпіади мають бути заздалегідь записані на класних дошках. Найкраще, якщо їх надрукувати на комп’ютері чи зробити ксерокопії для кожного школяра.

Розв’язання задач учні записують на окремих сторінках учнівського зошита, дозволяється користуватися чернетками. Час виконання роботи - 40-50 хвилин. Задачі можна виконувати у будь-якому порядку. Хто впорається з усіма завданнями, може подумати і над резервними, записати їх розв’язання.

Учасниками шкільних олімпіад є третина учнів класних олімпіад - їх переможці. Завдання шкільної олімпіади пропонується в одному варіанті, але її учасники мають сидіти за окремими партами чи столами. Якщо у школі є багато паралельних класів, то учасників шкільної олімпіади варто розподілити на дві чи три групи. Але олімпіаду провести в один день.

Досвід проведення математичної олімпіади у 1 класі підтвердив доцільність такої форми роботи. Олімпіади подобаються, зацікавлюють і дітей, і батьків. Вчителю допомагають намітити, які завдання варто опрацювати на уроці додатково, і якими новими, оригінальними (часто запропонованими учнями) методами можна розв’язати задачу чи приклад. Цей вид математичних змагань сприяє розвитку не тільки математичних здібностей, а й самостійності, впевненості, старанності учнів. Його варто починати практикувати з першого класу. Проведення математичної олімпіади є підсумком вивченого матеріалу, набутих знань, умінь і навичок.

Математичний ранок.

Досить цікавим є такий вид позакласної роботи з математики як математичний ранок.

Проводиться з метою заохочення дітей до предмету, демонстрації умінь та навичок дітей, отриманих на уроках та інших позакласних заходах для батьків дітей, учителів та учнів інших класів.

Ранок може відбуватися в класі або в шкільному залі. Приміщення святково прикрашається. Проводиться ранок у двох паралельних класах, або один клас ділиться на дві групи.

Зміст і форми математичних ранків бувають різні, але треба домагатися, щоб кожен учень був не тільки глядачем свята, а й активним його учасником. Найчастіше при проведенні математичних ранків організовують змагання кількох команд, ставлять інсценівки із залученням казкових героїв, розв’язують задачі казкового характеру, задачі-жарти і т.д.

Необхідно визначити премії переможців. Це можуть бути кольорові листівки, грамоти тощо. Але бажано, щоб кожен учень отримав сувенір, наприклад, книжку з цікавими задачами і вправами з математики для даного класу.

Зміст позакласних заходів потрібно добирати так, щоб дати можливість учням вивчати в більш ранньому віці елементи сучасної науки в доступній та цікавій для них формі. Як правило, їх проводять систематично, за заздалегідь продуманим планом. Але це не виключає епізодичного проведення, особливо в 1 і 2 класах, окремих заходів: математичних ігор, годин цікавої математики та ін.

2.2 Розробка і обґрунтування системи позакласних занять у формі годин цікавої математики

Позакласна робота з математики у початкових класах проводиться для того, щоб зацікавити дітей до вивчення цього предмету вже з перших років навчання. Однією з форм цієї роботи є години цікавої математики, на доцільність використання яких і спрямоване наше дослідження та експеримент.

Ми розробили систему годин цікавої математики для 3-ого класу. За нашою системою вони проводяться систематично - один раз на місяць, в перший тиждень місяця.

Кожна година цікавої математики несе в собі цікаву інформацію, яка не входить в навчальний матеріал; містить цікаві задачі й загадки, які потребують від дітей швидкого мислення, добре розвинутої логіки. Дітям подобається щось нестандартне, тому їм цікаво на таких заняттях. А часто знання, які вони отримують на таких позакласних заняттях, стають у пригоді їм в повсякденному житті, що теж тішить учнів. Отже, години цікавої математики займають досить значну роль у зацікавленні дітей до вивчення цієї потрібної в житті науки.

Розглянемо розроблену нами систему годин цікавої математики. Кожне заняття містить теоретичну частину - цікавий матеріал, що або стосується окремої теми, або просто підібраний з пізнавальною метою для дітей і стосується математики. Також в заняття входить практична частина, що містить цікаві завдання, підібрані як до теоретичного матеріалу, так і просто для загального розвитку дітей.

Заняття 1.

(5 вересня)

"Про знаки арифметичних дій, рівності та нерівності."

З‘явилися вони, ці знаки, у такому вигляді, як ми їх знаємо, з поширенням у Європі арабського написання чисел. Звичайно, не всі зразу.

Першими народилися знаки додавання "+" і віднімання "-". Їх наприкінці XV століття застосував лейпцігський професор Ян Відман у творі "Швидка і красива лічба для всього купецтва".

Але ж люди вміли віднімати і додавати раніше! Як же позначали ці дії на письмі? У різних народів по-різному. Єгиптяни, наприклад, коли хотіли додати два числа, схематично малювали дві людські ноги, що "рухалися" вперед, а при відніманні ступні цих ніг скеровували в зворотному напрямку. У стародавніх греків додавання позначали вертикальною рискою, а віднімання - значком, схожим на кому. У Європі дію додавання ще позначали літерою "р" або "Р" (початкова літера латинського слова "плюс" - більше), а віднімання "m" або "М" (від латинського "мінус" - менше). Однак ці позначення не прижилися.

Знак множення "X" - навскісний хрест - знаходимо у праці англійського математика Уїльяма Оутреда "Математичний ключ" (1631-й рік). Згодом, у 1698 році, видатний німецький математик Готфрід-Вільгельм Лейбніц дію множення запропонував передавати крапкою (×), а трохи раніше, у 1684 році, впровадив дві крапки (:) для позначення ділення. Щоправда, ці знаки дістали загальне визнання і набули поширення лише у XVIII столітті завдяки підручникам німецького математика Крістіана Вольфа.

Знак рівності "=" ввів англійський учений Роберт Рекорд ще в XVI столітті. На його думку, ніщо не може передати рівність так, як два однакових паралельних відрізки. До нього в математиці користувалися іншими знаками рівності. Так, старогрецький математик Діофант відношення рівності позначав літерою "і" (початкова у слові "ізос" - рівний). Індійські і арабські математики, а також більшість європейських найчастіше, аж до XVII століття, вживали для цього повністю або скорочено слово "рівний".

Знаки " < " і " > " для позначення відношень нерівності систематично почав застосовувати англійський математик Томас Гаррієт. Його книжка, де він вживає ці знаки, побачила світ у 1631 році.

Дужки круглі знаходимо у математичних творах першої половини XV століття. До їхньої появи ставили риски над виразом, якого вони стосувалися, або ж під ним, що було дуже незручно під час друкування.

Знак ділення й дробу - горизонтальна риска - вперше зустрічається у італійського математика Леонардо Пізанського, який, мабуть, запозичив його з арабських рукописів. Для зручності в друкуванні англієць Август де Морган замінив горизонтальну риску навскісною.

Алфавіт сучасної математичної мови складається:

з грецьких, латинських та німецьких готичних букв; літер кирилиці;

з арабських та римських цифр;

з граматичних знаків;

з математичних знаків;

з деяких інших знаків.

Ось такі цікаві історії про наші математичні знаки. А зараз ми ще спробуємо трішки поміркувати.

Я читаю вам завдання, а ви старайтесь чимшвидше дати на нього відповідь.

1) До двоцифрового числа приписали зліва цифру 2. Як змінилося число? (Збільшилося на 200).

2) Сказати найменше трицифрове число, у якого всі цифри різні. (102)

3) Назвіть всі трицифрові числа, після зменшення яких у два рази утворюється знову трицифрове число, але з однаковими цифрами. (222, 444, 666, 888)

А тепер задачі на кмітливість:

1. Син мого батька, а не брат мені. Хто це? (Я сам)

2. Скільки у сім’ї дітей, якщо у кожного брата сестер і братів порівну, а в кожної сестри братів удвічі більше, ніж сестер? (7 дітей: 4 брати, 3 сестри).

3. Складіть з паличок або сірників таку фігуру і заберіть 4 палички так, щоб залишилось 3 квадрати.

Заняття 2.

(10 жовтня. До теми "Доба. Година. Хвилина. Секунда. Визначення часу за годинником.")

"Перший годинник".

Ми звикли до годинника. Навіть не віриться, що колись люди не знали його. А такий час був. Наші далекі предки розпізнавали тільки ніч, ранок, день і вечір. Потім час вимірювали за довжиною тіні. Подовжилась тінь людини на три ступні - незабаром вечір. Ти маєш прийти в гості "у чотири ступні" - чекай, бо ще рано. Проте цей спосіб був незручний: ступні ж у людей неоднакові, до того ж взимку тінь довшає швидше, ніж улітку. Треба було шукати іншого способу. І його, нарешті, було знайдено. На рівному, відкритому для сонця майданчику вкопали палицю, обвели колом і стали уважно спостерігати за рухом її тіні. Це був перший сонячний годинник. З часом його удосконалили.

Годиннику було дано назву гномон (від грецького "стовпчик"). У стародавньому Вавілоні на вершині найбільшої піраміди поставили глиняний стовп. Рівний майданчик під ним розкреслили на однакові сегменти. Коли тінь від сонця наближалася до однієї з ліній, жрець проголошував: "Волею бога минула ще одна голина від сходу сонця!"

За переказами, перший механічний годинник з’явився 996 року в давньому німецькому місті Магдебурзі. До нашого часу зберігся годинник на башті Вестмінстерського абатства в Лондоні. Ще у XIII столітті він показував час жителям цього міста.

На початку XVI століття нюрнберзький винахідник Петер Генлейн змайстрував кишенькового годинника, який називали "нюрнберзьке яйце". Через півстоліття годинник отримав хвилинну стрілку, а ще через двісті років - секундну.

Російські вмільці майстрували механізми не гірше від зарубіжних колег. Талановитий винахідник і механік Іван Петрович Кулібін, який жив у кінці XVIII століття, створив справжнє чудо техніки: його годинник показував і відбивав цілі години, половини і чверті.

Золоті руки були у Кулібіна, але, як і багатьом російським винахідникам, йому випала нелегка доля. Зараз його творіння виставлене в Ермітажі.

Опівночі, в кожну оселю Росії, долинає бій Кремлівських курантів. Шість століть вони ведуть рахунок часу.

Ось яка історія виникнення годинника. А зараз цікаві завдання.

1. Котра зараз година, якщо частина доби, яка залишилася, у 2 рази менша від тієї, що минула? (16-та година)

2. Стінний годинник відбиває цілі години і ще одним ударом кожні півгодини. Скільки ударів на добу робить цей годинник?

3. Сергійко думав, що прийшов на зустріч на 15 хв раніше від її початку, але його годинник відставав на 10 хв, а початок зустрічі затримався на 20 хв. Скільки часу чекав Сергійко початку зустрічі?

А зараз ми пограємо у дуже цікаву математичну гру. Називається вона "Ой" або "Не зіб’юсь".

Правила гри: зараз ми всі станемо в коло і будемо називати всі числа по порядку так, як стоїмо. Але є одна умова. Ми не повинні називати числа 2 і числа, куди входить цифра 2, а замість нього кажемо "Ой". Хто зіб’ється, той виходить з гри.

Заняття 3.

(14 листопада)

"Коротка мандрівка в історію чисел і цифр"

Кількасот років тому з цифрами мало справу небагато людей: вчені, збирачі податків, купці тощо. Нині ж цифри постійно нагадують нам про себе. Відрізки часу, температура повітря, номер будинку і квартири, номер школи тощо - все позначається цифрами.

Цифри - це символи чисел, знаки, за допомогою яких числа передають на письмі. Перше народилися числа, а вже потім - цифри. Спочатку люди навчилися лічити, "винайшли" число, а тоді знайшли спосіб записувати результати лічби.

Як же виникла лічба? З давніх-давен люди дошукувалися відповіді на це запитання. І в різних народів відповідь була однакова. Стародавні греки, наприклад, вважали, що людей навчив лічити Прометей. Той самий, що за легендою викрав у богів вогонь і віддав його людям. Взагалі більшість народів появу числа пов’язувала з "діяннями" богів або ж міфічних героїв. Щоправда, інколи цю заслугу приписували людям, які насправді жили колись. Автори староруських рукописів, наприклад, вважали, що лічбу винайшов Піфагор - старогрецький математик, який жив у VI столітті до нашої ери. Піфагор був великим математиком, але ж люди вміли лічити задовго до VI століття! І не просто вміли лічити, але й мали вчених, які писали математичні книги. Найдавніша математична книга дійшла до нас з другого тисячоліття до нашої ери. І цілком можливо, що книжки, написані ще раніше, до нас просто не дійшли…

Доведено, що був час, коли люди обходились без чисел. Наприклад, мешканці австралійських джунглів, бажаючи обмінятися продуктами, чинили так. Люди одного племені клали на землю в’язки їстівного коріння, а другого - навпроти кожної такої в’язки ставили кошик з рибою. Встановивши відповідність рівночисельних множин, провадили обмін.

Можна назвати винахідника, який сконструював ту чи іншу машину, можна назвати вченого, який відкрив той чи інший закон природи, але ніхто не може назвати того, хто поклав початок лічбі. Уміння лічити прийшло до людей з життєвим досвідом. Саме життя спонукало людину до цього.

Не можна назвати імені й того, хто навчив людей записувати результати лічби. Але ми можемо напевне сказати, що сталося це тоді, коли люди вже вміли писати.

Спочатку кількість передавали за допомогою малюнка. Приміром, щоб показати число 1, малювали 1 палець, 2 - два пальці, 10 - з’єднані руки, 100 - згорнуту вимірну мотузку, 1000 - квітку лотоса. Взагалі квітка лотоса була символом великого числа. Цей спосіб запису чисел застосовували в стародавніх країнах - Єгипті і Китаї. Греки ще в V столітті до нашої ери назвали такі знаки ієрогліфами - "священним різьбленням".

З розвитком писемності, зокрема буквеного письма, числа почали записувати словами. Спочатку записували повністю, потім скорочено, використовуючи лише першу літеру числівника. Стародавні математики прийшли до висновку: це не дуже зручно, і от у V столітті до нашої ери зароджується нова, алфавітна система нумерації: першими дев’ятьма літерами позначали одиниці (від 1 до 9), наступні дев’ять літер використовувалися для позначення десятків (від 10 до 90), а ті, що йшли за ними, дев’ять літер - для позначення сотень (від 100 до 900).

Проте у щойно згаданих систем нумерації - ієрогліфічній та алфавітній - був один досить суттєвий недолік: ієрогліфічні знаки й літери не мали чітко визначеного місця - позиції. Такий запис дуже ускладнював обчислення. Щоправда, ще у стародавньому Вавілоні, де користувалися своєрідним письмом - клинописом і де числа позначали тими ж значками-клинцями, вже намагалися закріпити за одиницями, десятками, сотнями певне місце. До цього вавілонян змушувала обмежена можливість їхнього письма. Клинці є клинці, багато їх не вигадаєш! От і додумалися закріпити за певними розрядами чисел певне місце. Значно пізніше, з другого століття нової ери, цю спробу самостійно почали розвивати в Греції, а незабаром позиційний запис чисел удосконалюють в Індії. Саме індійська система лягла в основу нашої нинішньої системи числення.

Систему числення, основану на позначенні всіх натуральних чисел десятьма знаками - цифрами, вперше описав і застосував у IX столітті талановитий син узбецького народу Магомет син Муси із Хорезму в рукописі "Арифметика індорум".

У Європі нова система нумерації стала відома на початку XIII століття завдяки італійському вченому Леонардо Пізанському, який описав її в 1202 році у своїй праці "Книга обчислень". Але утвердилася ця система в Західній Європі значно пізніше - у XV-XVI століттях.

На Русі про арабсько-індійську систему знали ще в XIII столітті. Так, на одному знайденому дзвоні, виготовленому у ті часи, знаходимо цю нову нумерацію. На початку XVII століття цими цифрами вже нумерують сторінки російських книг, їх карбують на золотих монетах. А в середині століття ними користуються в рукописних працях. В 1703 році в "Арифметиці" Леонтія Магницького, тій самій, з якої черпав свої перші знання з математики великий російський учений Михайло Ломоносов, усе арифметичне вчення викладене на основі позиційної системи числення, і тільки сторінки підручника позначені слов'янською нумерацією.

Наша мандрівка продовжиться на наступному занятті. А зараз розгадаємо декілька веселих віршованих загадок:

Три білки і сім зайчаток

Мов зграйка хлоп’ят і дівчаток.

Всі стали в кружок,

Пустилися у танок.

Підбігли ще до них

Шість мишок лісових.

Які ж прудкі звірята!

Лічімо їх, хлоп’ята.

Встала вранці мишка-мати

Дітям зерна роздавати.