Задача трудового обучения – развитие творческого мышления

2.3. Задача трудового обучения – развитие творческого мышления.

Одна из задач уроков трудового обуче­ния — развитие у детей младшего школь­ного возраста творческого мышления и во­ображения. В методической литературе приводятся некоторые виды творческих заданий, предлагаемых на уроках труда. Они могут быть связаны, например, с из­менением конструкции изделия, а именно: формы, размеров, количества, способов соединения комплектующих деталей; с за­меной материалов и с различным оформ­лением изделия.

В настоящей статье мы хотим рассмо­треть задания творческого характера на этапе работы с чертежами и графически­ми картами, а также предложить в по­мощь учителю возможные способы раз­метки к некоторым изделиям.

Обратимся к самому распространенно­му на уроках труда виду работы с бумагой и картоном — аппликации из геометричес­ких фигур. Эти работы выполняются уча­щимися начальной школы в разных классах в зависимости от дидактических целей и сложности конструкции изображения.

При изготовлении аппликаций из гео­метрических фигур у детей совершенству­ются навыки разметки, приемы работы с ножницами и клеем; решаются задачи сен­сорного развития учащихся, так как, рас­членяя сложные фигуры на простые и, на­оборот, составляя из простых фигур более сложные, школьники закрепляют и углуб­ляют свои знания о геометрических фигу­рах, учатся различать их по форме, величи­не, цвету, пространственному расположе­нию. Кроме того, эти уроки дают возмож­ность знакомить младших школьников с различными техническими объектами (ма­шинами, орудиями труда), их применением в народном хозяйстве, устройством, прин­ципом действия, а также с технической терминологией. Занятия с элементами пло­скостного конструирования способствуют в дальнейшем изготовлению объемных мо­делей технических устройств. Та­ким образом, эти занятия открывают воз­можность для развития творческого конст­рукторского мышления.

Изображения в данном случае носят силуэтный характер. Однако аппликации можно сделать и цветными, если органи­зовать работу в парах, т.е. обменяться ка­кой-либо деталью (деталями) другого цве­та с соседом по парте. Возможен и дру­гой вариант — перевернуть деталь нео­крашенной стороной (рис. 2).

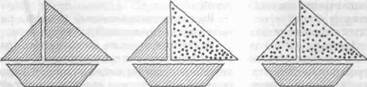
Парусник (рис. 1а) — одна из первых аппликаций из геометрических фигур, ко­торую можно изготовить с первоклассни­ками, Необходимо организовать деятель­ность учащихся на уроке таким образом, чтобы она развивала воображение детей. В данном случае у них должен возникнуть образ парусника на основе предложенного графического изображения его деталей.

Для первоклассников эту работу лучше организовать в игровой форме. Учитель может создать ситуацию с любимым геро­ем какой-либо сказки или мультфильма. Например: у Айболита, который в Африке лечит обезьян, кончились лекарства, и ему нужно помочь — отвезти новые.

— Кто помнит, как добирался Айбо­лит до Африки? (Плыл на корабле.)

— Значит, и нам предстоит плыть. Ка­кие средства передвижения по воде вы знаете? (Плот, лодка, корабль, катер, вод­ный велосипед и др.)

— У вас на столах лежат квадраты цветной бумаги, из которых нужно будет построить то, на чем мы поплывем.

— Посмотрите на доску. Какая фигу­ра здесь изображена? (Квадрат.)

— На какие фигуры разделен квадрат? (На два треугольника и четырехугольник.) Это детали будущего изделия.

— Сколько всего геометрических фи­гур в квадрате, т.е. в заготовке изделия? (Три.) Есть ли одинаковые? Какие? (Тре­угольники.) Чем они отличаются друг от друга? (Размером.)

— На части какого плавающего сред­ства похожи эти геометрические фигу­ры? Посмотрите на четырехугольник. Что он вам напоминает? (Лодочку.)

— На что похожи треугольники? (На паруса.)

Далее следует выставить готовый об­разец аппликации или техникой мокрых деталей собрать на доске изображение парусника (смочить в воде заранее заго­товленные детали из бумаги и приклеить на доску.)

— Покажите на аппликации и назови­те части парусника. (Корпус, большой па­рус и маленький парус.) Какую форму они имеют?

— Покажите на рисунке большой па­рус. Маленький парус. Корпус.

Таким образом, анализ чертежа и со­отнесение геометрических форм с частя­ми реальных технических объектов поз­волили создать образ парусника.

В любой работе учителю важно выде­лить то главное, что поможет детям вос­создать необходимый образ. В данной ра­боте таким ключевым моментом является вопрос о том, на что похож четырехуголь­ник. При этом существенным может ока­заться даже пространственное располо­жение чертежа, отражающее более или менее естественное положение фигуры в пространстве (четырехугольника) и помо­гающее увидеть в этой фигуре образ бу­дущего объекта (лодочку).

К тому же оба варианта разметки ква­драта могут быть использованы на уроке как задание на развитие воссоздающего воображения. Например: какая лодочка — на берегу, а какая — в море? Почему?

Заготовка деталей аппликации начина­ется с разметки. Разметка — исходная, ос­новная операция при изготовлении любо­го изделия. От того, насколько точно и правильно она выполнена, зависит качест­во работы. При этом нужно отметить, что разметка — одна из сложнейших опера­ций как для учащихся, в силу их возраст­ных особенностей, так и для учителя, по­скольку в литературе, где предлагаются конкретные практические работы, дается только чертеж и в лучшем случае указы­вается порядок изготовления изделия. А то, каким способом выполнять разметку по данному чертежу, — решать учителю.

Очень важно знать все способы раз­метки и владеть ими, чтобы выбрать наи­более рациональный, приемлемый, до­ступный.

Рассмотрим возможные способы раз­метки деталей аппликации парусника.

Во-первых, можно использовать раз­метку сгибанием с последующим разреза­нием заготовки по линиям сгиба. В I клас­се, особенно в первом полугодии, дети еще не умеют пользоваться чертежными инст­рументами и не владеют необходимым ма­тематическим материалом. Поэтому раз­метка сгибанием, где вычерчивание линий заменяется линиями сгибов, часто исполь­зуется уже в начале учебного года (рис. 2).

Однако нужно помнить, что данный прием несколько снизит качество аппли­кации, так как резать по сгибу неудобно, ровный разрез получить трудно.

Во-вторых, для разметки можно ис­пользовать и линейный шаблон (полоску картона нужной ширины). Шаблоном мо­жет служить также обычная линейка. В этом случае несколько изменятся пропор­ции деталей (корпус лодочки уменьшится, т.е. будет уже, а маленький парус соответ­ственно увеличится), но для данной апп­ликации это несущественно.

В-третьих, разметку можно выполнить и с помощью линейки. Однако для уча­щихся I класса это будет самый сложный вариант. Разметка диагонали сама по себе не вызовет у детей затруднений, так какне требует разметки точек — достаточно только провести по линейке линию из уг­ла в угол. Сложнее разметить вторую ли­нию, так как нужно найти и отметить точ­ками середину сторон квадрата, а затем по линейке соединить найденные точки. Важ­но учитывать размер заготовки, чтобы при делении стороны квадрата пополам полу­чилось целое количество сантиметров.

Далее рассмотрим задание творческо­го характера на примере изготовления аппликации ракеты. В этом случае зада­ние требует от детей деятельности на восстановление недостающих линий чер­тежа. На начало работы учащимся пред­лагается образец изделия и неполная схе­ма деления квадрата .

Анализ данного образца и построение чертежа к нему можно организовать сле­дующим образом.

— Ребята, для того чтобы вы смогли собрать такую ракету (показ образца), я сделала на доске чертеж ее деталей. Но злая колдунья Ундина решила вам поме­шать и испортила его: стерла несколько линий. Перед нами встала задача восста­новить их.

Посмотрите на аппликацию. Из ка­ких геометрических фигур построен кор­пус ракеты? (Из квадрата и прямоуголь­ника.) Покажите их.

— Какую форму имеет нос ракеты? (Форму треугольника.) Ступени? (Тоже треугольники.) Чем они отличаются друг от друга? (Размером.) Сколько всего треуголь­ников использовано в аппликации? (Три.)

— Посмотрите на рисунок, Какую форму имеет заготовка, из кото­рой будем собирать ракету? (Форму ква­драта.)

— На какие фигуры разделен квад­рат? (На прямоугольники.) Сколько их? (Два.) Сколько прямоугольников нужно для изготовления ракеты? (Один.)

— Значит, из второго прямоугольника мы можем получить недостающие детали. Какие? (Нос, ступени и верхнюю часть корпуса ракеты.) Какую геометрическуюорму они имеют? (Форму квадрата и треугольников.)

— Как получить квадрат (? (Прямоугольник разделить пополам.) Сколько квадратов получилось? (Два.) Сколько нам нужно? (Один.)

— Какой формы детали нам нужно еще заготовить? (Треугольники.) Сколь­ко? (Три.) Какие? (Один большой и два маленьких.)

— Как из второго квадрата разметить треугольники? (Разделить по диагонали.) Сколько треугольников получили? (Два.)

— Какую часть ракеты можем офор­мить? (Нос.) Что осталось разметить? (Ступени.) Покажите, как вы это сделае­те Целесообразно, чтобы всю работу по разметке линий чертежа дети выполняли на доске сами.

Работа по разметке деталей ракеты немного сложнее парусника, так как ква­драт нужно разделить на большее коли­чество деталей, но способы разметки ана­логичны. Разметка сгибанием.

Порядок разметки и раскроя деталей указан в графической инструкционной карте (рис. 7).