Навигация
Проверочная работа
6. Проверочная работа.
Вариант №1
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
Вариант №2
1) ![]() ;
;
2) ![]() ;
;
![]() .
.
Критерии оценивания:
«5» - верно выполнены все задания;
«4» - верно выполнены любые два задания;
«3» - верно выполнено любое одно задание.
Занятие №5 Тема: «Использование понятия области изменения функции при решении уравнений».
Цели:
а) изучить теоретический материал по теме «Использование понятия области изменения функции при решении уравнений»;
б) познакомить с основными способами определения множества значений функции.
Ход занятия:
1. Проверка домашнего задания. На доске записывается ответ к каждому заданию. Если у большинства учащихся есть затруднения в решении, то задание разбирается на доске. Если задание вызвало затруднение у небольшой группы учащихся, то к каждому из них «приставляется» ученик, выполнивший задание, с целью объяснить решение.
2. Лекция по теме «Использование понятия области изменения функции при решении уравнений».
Утверждение 1. Пусть дано уравнение ![]() , причем функции
, причем функции ![]() как правило разнородные. Если множества значений этих функций имеют общую точку (или небольшое конечное число общих точек)
как правило разнородные. Если множества значений этих функций имеют общую точку (или небольшое конечное число общих точек) ![]() ;
; ![]() , то уравнение равносильно системе
, то уравнение равносильно системе ![]() .
.
В системе можно решить только одно уравнение, а второе проверить подстановкой получившихся корней.
Утверждение 2. Если области изменения функций, входящих в уравнение (неравенство), не имеют общих точек, то уравнение (неравенство) решений не имеет.
Существует несколько способов определения множества значений функций. Рассмотрим их на примерах.
Пример 1. Найти область изменения функции ![]() .
.
Для решения задачи построим схему графика с помощью производной:
1) область определения функции y промежуток ![]() ;
;
2) с помощью производной найдем экстремумы. В точке ![]() функция принимает свое максимальное значение;
функция принимает свое максимальное значение;
3) найдем значения функции в точке максимума и на концах отрезка области определения: ![]() ;
; ![]() ;
; ![]() .
.
4) таким образом, получаем ![]() .
.
Пример 2. Найти область изменения функции ![]() .
.
Преобразуем функцию к виду ![]() .
.
Область изменения этой функции находится непосредственно: ![]() .
.
Для нахождения множества значений некоторых тригонометрических функций удобно пользоваться следующим фактом.
Утверждение 3. Функция вида ![]() изменяется на отрезке
изменяется на отрезке ![]()
Пример 3. Найти область изменения функции ![]() .
.
Введем замену ![]() и рассмотрим функцию
и рассмотрим функцию ![]() ,
, ![]() . Ее область изменения с помощью производной найти гораздо проще.
. Ее область изменения с помощью производной найти гораздо проще. ![]() .
.
Рассмотрим на примере, как при решении уравнений знание области изменения функций, в него входящих, упрощает поиски корней.
Пример 3. Решить уравнение ![]()
Рассмотрим функции, стоящие в левой и правой частях уравнения, ![]() . Найдем их множество значений
. Найдем их множество значений ![]() . Воспользуемся утверждением 1: так как множества значений имеет общую точку 2, от уравнения можно перейти к системе
. Воспользуемся утверждением 1: так как множества значений имеет общую точку 2, от уравнения можно перейти к системе 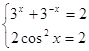 . Решением системы, а, значит, и исходного уравнения является
. Решением системы, а, значит, и исходного уравнения является ![]() .
.
Утверждение 4. Пусть дано неравенство ![]() . Если множества значений этих функций имеют общую точку
. Если множества значений этих функций имеют общую точку![]() ;
; ![]() , то неравенство равносильно системе
, то неравенство равносильно системе ![]() .
.
Пример 4. Решить неравенство ![]() .
.
ОДЗ неравенства есть все действительные x, кроме -1. Разобьем ОДЗ на три промежутка ![]() и рассмотрим неравенство на каждом из этих промежутков. На первом и третьем промежутках неравенство выполняется для любого x:
и рассмотрим неравенство на каждом из этих промежутков. На первом и третьем промежутках неравенство выполняется для любого x: ![]() (
(![]() );
); ![]() (
(![]() );
); ![]() (
(![]() ). Следовательно, оба промежутка являются решением неравенства. На втором промежутке
). Следовательно, оба промежутка являются решением неравенства. На втором промежутке ![]() , то есть неравенство решений не имеет. Исходя из этого получаем решением неравенства
, то есть неравенство решений не имеет. Исходя из этого получаем решением неравенства ![]() .
.![]()
3. Постановка домашнего задания.
1) Выучить теоретический материал.
2) Найти множество значений функций:
а)![]() ; б)
; б) ![]() .
.
3) Решить уравнение ![]() .
.
Занятие №6 Тема: «Использование понятия области изменения функции при решении уравнений».
Цель: закрепить знания по теме «Использование понятия области изменения функции при решении уравнений».
Ход занятия:
Похожие работы
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...
... образом: «Показательно-степенные уравнения и неравенства». Целями настоящей работы являются: 1. Проанализировать литературу по данной теме. 2. Дать полный анализ решения показательно-степенных уравнений и неравенств. 3. Привести достаточное число примеров по данной теме разнообразных типов. 4. Проверить на урочных, факультативных и кружковых занятиях ...

0 комментариев