Навигация
Проверка домашнего задания. До начала занятия один из учеников записывает домашнее задание на доске учитель и другие ученики проверяют решение
1. Проверка домашнего задания. До начала занятия один из учеников записывает домашнее задание на доске учитель и другие ученики проверяют решение.
2. Решение задач. На доске написан список задач. Учащиеся по одному решают у доски. Учитель напоминает, что данные уравнения и неравенства решаются с использованием множества значений функций, в них входящих.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
3. Подведение итогов занятия.
Учитель выставляет баллы за занятие: 1 балл за решение домашнего задания, по одному баллу за решение задач у доски
4. Постановка домашнего задания
Решить уравнения и неравенство:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Занятие №7 Тема: «Использование неотрицательности функций, входящих в уравнение или неравенство».
Цели: познакомить учащихся с приемом решения уравнений и неравенств, состоящих из неотрицательных функций.
Ход занятия:
1. Проверка домашнего задания. На доске записывается ответ к каждому заданию. Уравнение, вызвавшее трудности, разбирается учеником, выполнившим его.
2. Изучение нового материала.
Утверждение 1. Пусть имеется уравнение ![]() . Если множество значений каждой из функций
. Если множество значений каждой из функций ![]() принадлежит промежутку
принадлежит промежутку ![]() , то уравнение равносильно системе
, то уравнение равносильно системе 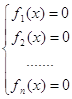 .
.
‑Назовите функции, которые принимают неотрицательные значения на всей области определения (![]() ).
).
Пример1. Решить уравнение ![]() .
.
Преобразуем уравнение ![]() . Наше уравнение будет равносильно системе
. Наше уравнение будет равносильно системе 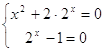 , которая не имеет решений. Значит и исходное уравнение решений не имеет.
, которая не имеет решений. Значит и исходное уравнение решений не имеет.
Аналогичное утверждение можно сформулировать и для неравенств.
Утверждение 2. Пусть имеется неравенство ![]() . Если множество значений каждой из функций
. Если множество значений каждой из функций ![]() принадлежит промежутку
принадлежит промежутку ![]() , то неравенство равносильно системе
, то неравенство равносильно системе 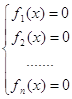 .
.
Пример 2. Решить неравенство ![]() .
.
Так как для любого x справедливы неравенства ![]() , то неравенство равносильно системе
, то неравенство равносильно системе 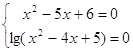 , решением которой является
, решением которой является ![]() . Значит, неравенство имеет единственное решение
. Значит, неравенство имеет единственное решение ![]() .
.
Утверждение 3. Пусть имеется неравенство ![]() . Если множество значений каждой из функций
. Если множество значений каждой из функций ![]() принадлежит промежутку
принадлежит промежутку ![]() , то решениями неравенства являются все x из ОДЗ, за исключением тех x, которые являются решениями системы
, то решениями неравенства являются все x из ОДЗ, за исключением тех x, которые являются решениями системы 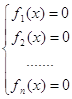 .
.
Пример 3. Решить неравенство ![]()
ОДЗ неравенства ![]() . Для нахождения решения неравенства нужно исключит из его ОДЗ все решения системы
. Для нахождения решения неравенства нужно исключит из его ОДЗ все решения системы ![]() . Решениями неравенства являются все x из множества
. Решениями неравенства являются все x из множества ![]() .
.
3. Решение задач. На доске написаны два варианта заданий. Учащиеся в течение 13-15 минут решают каждый свой вариант, затем в паре обмениваются тетрадями и проверяют решение соседа по парте и ставят баллы (по одному за каждое верное решение уравнения или неравенства). Учитель выписывает ответы на доске.
Вариант 1.
1) ![]() ;
;
2) ![]() ;
;
3) 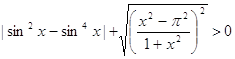 .
.
Вариант 2.
1) ![]() ;
;
2) ![]() ;
;
3) 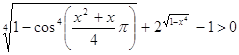 .
.
4. Подведение итогов занятия. Учитель выставляет баллы полученные учениками. 1 балл ставится ученику, объяснявшему домашнее задание.
5. Постановка домашнего задания
Решите уравнения и неравенство:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Занятие №8 Тема: «Использование свойств четности или нечетности и периодичности функций».
Цель: знакомство с новым приемом решения уравнений и неравенств – использование свойств четности, нечетности и периодичности функций.
Ход занятия:
Похожие работы
... -иллюстративного и репродуктивного метолов, а экономический профиль ориентирован на формирование прикладного стиля мышления. 2. Методика проведения элективных курсов по математике в профильной школе 2.1 Цели организации элективных курсов по математике Принципиальным положением организации школьного математического образования в настоящее время является дифференциация обучения ...
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...
... образом: «Показательно-степенные уравнения и неравенства». Целями настоящей работы являются: 1. Проанализировать литературу по данной теме. 2. Дать полный анализ решения показательно-степенных уравнений и неравенств. 3. Привести достаточное число примеров по данной теме разнообразных типов. 4. Проверить на урочных, факультативных и кружковых занятиях ...

0 комментариев