Навигация
Индивидуальная систематизация
1. Индивидуальная систематизация.
При индивидуальном контроле каждый ученик получает свое задание, которое он должен выполнить без посторонней помощи. Такая форма систематизации целесообразна в случае, если требуется выяснить индивидуальные знания, способности и возможности отдельных учащихся.
Такая форма систематизации всегда планируется: учитель намечает, когда, кого, с какой целью спросить и какие для этого использовать средства.
2. Групповая систематизация.
При проведении такой систематизации знаний класс временно делится на несколько групп (от 2 до 10 учащихся) и каждой группе дается проверочное задание. В зависимости от цели систематизации группам предлагают одинаковые или разные задания.[23, с. 13]]
Групповую форму систематизации применяют:
а) При повторении с целью обобщения и систематизации учебного материала.
б) При выделении приемов и методов решения задач
в) При выявлении наиболее рационального решения задач или доказательства теорем.
Иногда групповую систематизацию проводят в виде уплотненного опроса.
3. Фронтальная систематизация.
При фронтальном контроле задания предлагаются всему классу. В процессе этого систематизации изучается правильность восприятия и понимания учебного материала, вскрываются слабые стороны в знаниях учащихся, обнаруживаются недочеты, пробелы, ошибки в работах и ответах учащихся. Это позволяет учителю вовремя наметить меры по их преодолению и устранению.
Взаимная систематизация
Роль взаимного систематизации качества и эффективности учебной деятельности школьников трудно переоценить.
Он содействует выработке таких качеств личности, как честность и справедливость, коллективизм. Взаимная систематизация помогает также учителю осуществлять форму знаний учащихся. В массовой школе сравнительно часто используется взаимная форма организационной готовности к уроку (констатирующая взаимосистематизация выполнения домашнего задания) и частичная, эпизодическая взаимоформа знаний учащихся (рецензирование ответов на уроке, рецензирование письменных работ). Систематическая же взаимная форма знаний, умений, навыков применяется весьма редко. Остановимся на методике проведения этой формы.[5, с. 26]]
Каждый ученик получает карточку с вопросом, ответ на который он должен знать хорошо; на обороте карточки записаны фамилии нескольких учащихся и даты, когда они будут опрошены по этому вопросу. В каждый из указанных дней владелец карточки задает свой вопрос одному из учеников, в то же время он и сам должен ответить на вопрос, помещенный в карточке этого ученика. За день до формы учащиеся предупреждают друг друга, на какие вопросы им придется отвечать. Взаимоформа проводится обычно в последние три минуты каждого урока. За правильный ответ против фамилии (на обороте карточки) ученик ставит знак плюс, за неверный ответ или отказ отвечать – минус. Учитель периодически просматривает карточки взаимоформы. В тех случаях, когда оказывалось много минусов, проводилась дополнительная взаимоформа этих учеников во внеурочное время. В конце четверти проводится систематизационый опрос всех учащихся, который позволяет выяснить не только общий уровень их знаний, но и насколько справедливо и строго каждый из них спрашивал своих одноклассников.
Взаимоформа знаний значительно активизирует деятельность учащихся, повышает интерес к знаниям и даже нравится им. В ходе взаимного систематизации раскрываются индивидуальные особенности детей, их взаимоотношения с товарищами.
Самосистематизация
На хорошем уроке всегда есть своя сверхзадача, которая сводится к формированию этих навыков и меняется в зависимости от темы урока. В одном случае она состоит в обучении приемам анализа, умению видеть закономерности, ставить вопросы, делать выводы.
В другом - в формировании критического отношения учащихся к результатам своей работы, требовательности к себе. Постоянного внимания учителя требует и проблема воспитания у учащихся веры в свои способности. Известно, что многие ученики боятся приступать к решению задач, алгоритм решения которых им неизвестен. Иногда проявляется страх перед трудностями, неумение преодолевать их самостоятельно. Выход здесь только один – прививать учащимся умения и навыки самосистематизации. Это важно с воспитательной, психолого-педагогической точки зрения. Ведь при этом ученики фактически участвуют в управлении своей собственной учебной деятельностью. Это порождает у них удовлетворенность своими занятиями, своей работой, позволяет им поверить в себя, в свои познавательные способности, открывает простор для творческой инициативы и самостоятельности. Укажем приемы формирования критического отношения учеников к результатам своей работы. Учащимся предлагается рассмотреть решения ряда примеров и оценить их. Обычно эти решения содержат типичные ошибки, которые надо обнаружить. Иногда требуется выяснить, верен ли ответ к заданию. Навыки самосистематизации можно развивать и на занимательных задачах, основанных на обычной житейской смекалке. Их полезно рассматривать как в младших, так и в старших классах. Эти задачи привлекают внимание всех учащихся, даже тех, которые не имеют особых успехов в математике[23, с. 56].
Трудно удержать интерес учащихся к предмету, если преследуется единственная цель: научить школьников выполнять действия по данному образцу. Поэтому наряду с изучением алгоритмов возникает необходимость учить осознанному, творческому их применению. Приведем один распространенный прием такого обучения. Сразу после того, как учащиеся освоили все этапы алгоритма, им предлагается задача, которая решается по изученному алгоритму, но не самым рациональным способом. Более красивое решение получается, если не следовать алгоритму, а просто проанализировать условие задачи и сделать верные выводы.
На уроках геометрии иногда полезно “досочинить” задачу. Обычно для этого выбирают задачу из учебника на доказательство. Выписывают ее условие, а то, что надо доказать, придумывают сами.
Отметим еще несколько приемов работы учителя в формировании потребности в самоконтроле при обучении математике[11, с. 43].
1. Давать определение иногда имеет смысл не в окончательном виде. Более
содержательные беседы с классом получаются тогда, когда ученики предлагают свой вариант определения, который затем уточняется.
2. Почти все упражнения, которые предлагаются ученикам, сформулированы
позитивно (доказать, найти). Появились также упражнения и другого типа (верно ли, проверить), но их очень мало. И совсем нет упражнений на опровержение утверждений, в то время как они чрезвычайно полезны.
Упражнения такого типа легко получить из задач позитивных, особенно на доказательство.
3. Если ученик дал письменное решение задачи (на доске или в тетради) с
ошибкой, то в иных случаях не надо торопиться с выставлением оценки. Если есть возможность дать ему время на нахождение собственной ошибки, то ее нужно использовать. Если ошибка будет найдена, то оценку снижать не стоит.
4. Класс работает самостоятельно. Выборочно просматривая некоторые
решения, учитель видит разнообразные ошибки, наиболее поучительные из них стоит показать всем учащимся класса.
5. На уроке предложена задача и сразу ответ к ней. У кого-то получился
другой ответ. Не стоит спешить с помощью – окажем ее только тогда, когда самостоятельные попытки найти ошибку ни к чему не привели.
6. Весьма рискованный, но заслуживающий внимания прием.
Учитель берется с ходу решать достаточно сложную задачу, причем на доске. Если ее и удается решить, то вряд ли наилучшим способом. Ученики еще раз убеждаются, что первый вариант решения не всегда является наилучшим.
В результате проведения описанной работы у учащихся начинает формироваться потребность в самоконтроле.
Обычным способом организации самосистематизации в процессе обучения математике является указание ответа (известного заранее или сообщаемого учениками друг другу). Некоторым учащимся в случае трудоемких заданий вполне достаточно свериться с окончательным результатом. Другим требуется дать промежуточные ответы. Это помогает им самостоятельно выполнять учебные задания даже в тот момент, когда у них еще не выработаны прочные навыки.
Среди учебных заданий, стимулирующих самосистематизация в работе учащихся, определенное место занимают задания с программированным систематизацией. Такие задания позволяют увеличить интенсивность самостоятельной учебной работы учащихся, удобны для организации фронтальной работы и коллективного обсуждения полученных индивидуальных результатов.
Последовательно работая над привитием умений, связанных с систематизацией и самосистематизацией в математической деятельности учащихся, можно добиться заметных результатов. При этом растет общая математическая культура школьников, их работы и ответы становятся более грамотными.
Похожие работы
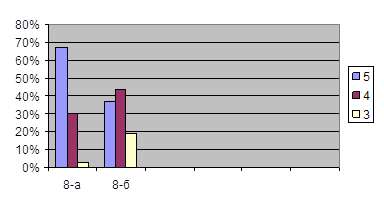
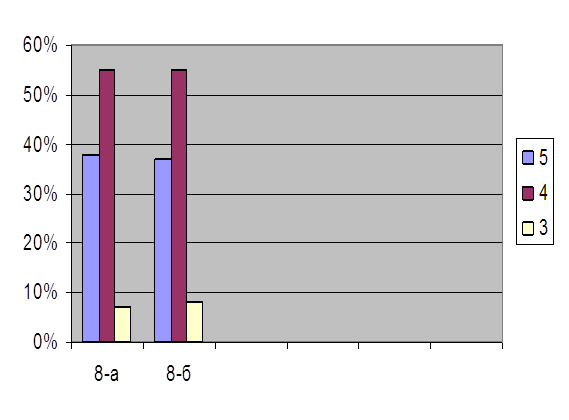
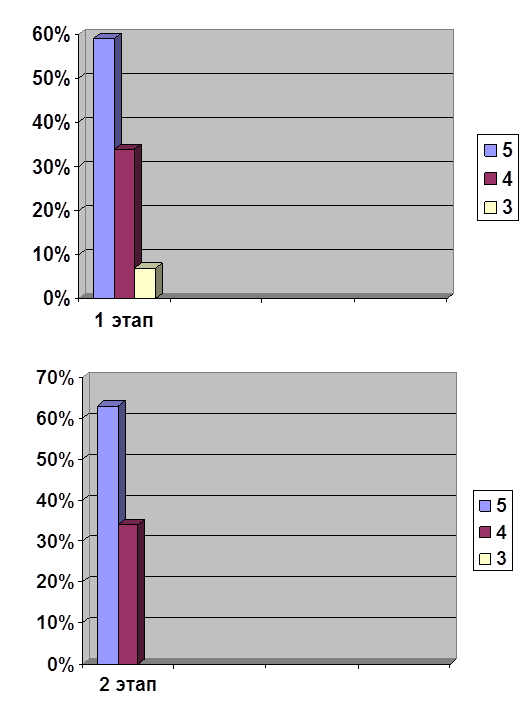
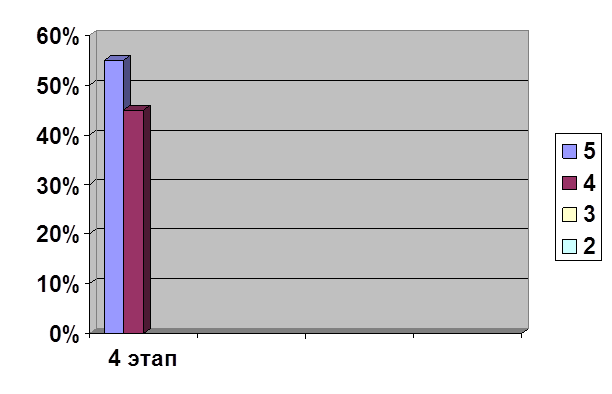
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
... Однако и в подростковом, и в старшем школьном возрасте имеются еще значительные резервы их совершенствования”.(22,С.108) ГЛАВА 3. Экспериментальная работа по формированию самоконтроля в процессе обучения математике по системе Эльконина- Давыдова. Наша работа посвящена изучению одного из структурных элементов учебной деятельности- изучению самоконтроля младших школьников. Перед началом проведения ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...

0 комментариев