Результаты эксперимента

2.3. Результаты эксперимента

Цель: Изучить уровень систематизации и обобщения полученных знаний на завершающем этапе эксперимента.

Для выявления влияния эксперимента, проведенного с детьми экспериментальной группы, мы провели эксперимент с учащимися систематизационной и экспериментальной групп. При этом использовались те же методики, что и в констатирующем эксперименте.

Таблица 1

Данные экспериментального изучения уровня систематизации и обобщения полученных знаний

Контрольная группа		Экспериментальная группа
Учащийся, №	Количество правильных ответов	Учащийся, №	Количество правильных ответов
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	7 5 5 5 3 3 3 5 3 5 3 3 3 3 3	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	8 6 5 6 7 4 5 4 5 3 3 3 4 3 3

По данным таблицы мы получили следующие результаты:

·          учащихся с высоким уровнем в контрольной группе 1 человек, в экспериментальной группе – 2 человека;

·          количество учащихся со средним уровнем в контрольной группе 5 человек, в экспериментальной – 8 человек;

·          учащихся с низким уровнем в контрольной группе 9 человек, в экспериментальной – 5 человек.

Контрольная группа:

F / N * 100%,

1/15*100% = 6,7%

5/15*100% = 33,3%

9/15*100% = 60%

Экспериментальная группа:

F / N * 100%,

2/15*100% = 13,3%

8/15*100% = 53,3%

5/15*100% = 33,4%

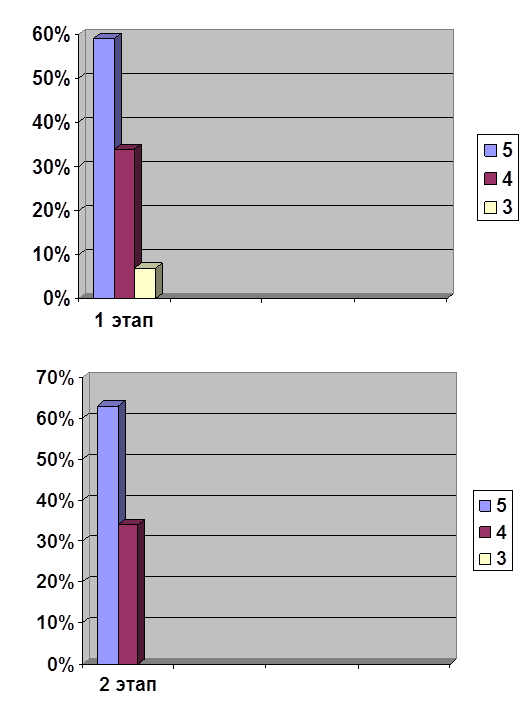
Результаты опроса представлены на рисунке 1.

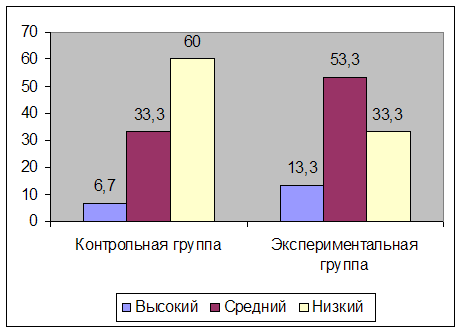Рис. 1. Выявление уровня систематизации и обобщения полученных знаний на стадии контрольного эксперимента по теме

 

«Алгебраические уравнения», 9 класс.

Из полученных данных мы видим, что высокий уровень составил в контрольной группе 6,7%, в экспериментальной – 13,3%. Средний уровень в контрольной группе – 33,3%, в экспериментальной – 53,3%, низкий уровень в контрольной группе 60%, в экспериментальной – 33,3%.

Таким образом, подводя итоги опроса, мы можем сделать вывод о том, что, говоря о систематизации и обобщении полученных математических знаний можно констатировать, что данный опрос показал, у учащихся 9 классов повысился уровень знаний по сравнению с итогами констатирующего эксперимента. Но, если сравнивать уровень знаний в контрольной и экспериментальной группах, то мы можем утверждать, что в экспериментальной группе уровень намного выше. Это было достигнуто благодаря использованию в нашем исследовании специализированных интегрированных уроков.

Таблица 2

Данные экспериментального изучения уровня сформированности знаний в контрольном эксперименте.

Контрольная группа		Экспериментальная группа
Учащийся, №	Количество правильных ответов	Учащийся, №	Количество правильных ответов
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	6 4 3 4 4 7 5 2 3 4 2 2 3 1 2	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	7 6 5 7 5 3 5 8 5 3 3 3 5 4 4

По данным таблицы мы получили следующие результаты:

·          учащихся с высоким уровнем в контрольной группе 1 человек, в экспериментальной группе – 3 человека;

·          количество учащихся со средним уровнем в контрольной группе 6 человек, в экспериментальной – 8 человек;

·          учащихся с низким уровнем в контрольной группе 8 человек, в экспериментальной – 4 человека.

Контрольная группа:

F / N * 100%,

1/15*100% = 6,7%

6/15*100% = 40%

8/15*100% = 53,3%

Экспериментальная группа:

F / N * 100%,

3/15*100% = 20%

8/15*100% = 53,3%

4/15*100% = 26,7%

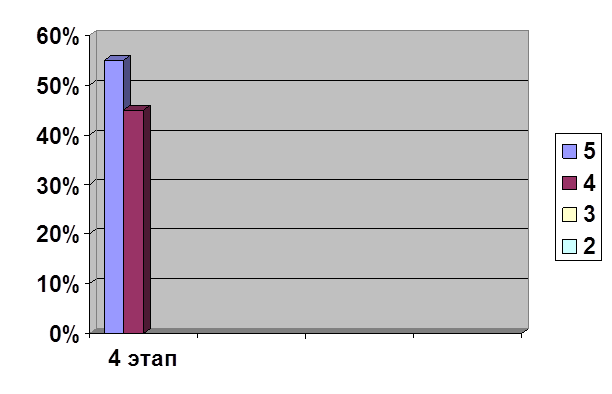
Результаты опроса представлены на рисунке 2.

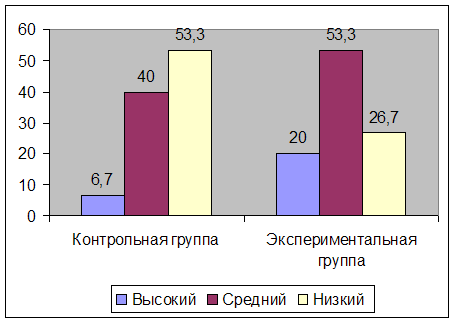
Рис. 2. Выявление уровня математических знаний учащихся на стадии контрольного эксперимента

Из полученных данных мы видим, что высокий уровень составил в контрольной группе 6,7%, в экспериментальной – 20%. Средний уровень в контрольной группе – 40%, в экспериментальной – 53,3%, низкий уровень в контрольной группе 53,3%, в экспериментальной – 26,7%.

Итак, анализ данных контрольного эксперимента показал, что уровень знаний возрос в обеих группах по сравнению с результатами констатирующего эксперимента. Но, если сравнивать показатели знаний в контрольной и экспериментальной группах, то уровень знаний в экспериментальной группе намного выше уровня знаний контрольной группы. Это стало возможным при использовании интегрированного урока.

Таким образом, проведенные нами исследования свидетельствуют о том, что, если систематически использовать такие формы систематизации и обобщения на уроках математики, как математический диктант, контрольные работы, а также проводить специализированные уроки, то:

·          расширяются и систематизируются представления школьников по предмету;

·          формируются навыки самосистематизации и обобщения знаний.

Заключение

 

Систематизация и обобщение знаний и умений учащихся – одно из основных условий повышения качества обучения. Учитель математики в своей работе должен использовать не только общепринятые формы систематизации (самостоятельная и систематизационная работы, устный опрос у доски и т.д.), но и постоянно изобретать, внедрять свои средства систематизации. Умелое владение учителем различными формами систематизации знаний и умений способствует повышению заинтересованности учащихся в изучении предмета, предупреждает отставание, обеспечивает активную работу каждого ученика. Систематизация для учащихся должна быть обучающей.

В результате проведения нетрадиционных форм систематизации знаний и умений раскрываются индивидуальные особенности детей, повышается уровень подготовки к уроку, что позволяет своевременно устранять недостатки и пробелы в знаниях учащихся.

Список литературы

 

1.         Амонашвили Ш. А. Обучение. Оценка. Отметки. – М.: Знание, 2004.

2. Баймуханов Б. Б. Тематический контроль и учет знаний // Математика в школе, 2006. - №5.

3.         Борода Л.Я. Некоторые формы систематизации знаний на уроке // Математика в школе, 2005. - №4.

4.         Вахламова А. П., Рабунский Е. С. О систематической взаимопроверке знаний учащихся на уроках // Математика в школе, 2004. - №1.

5.         Груденов Я. И. Совершенствование методики работы учителя математики – М: Просвещение, 2005.

6.         Дакацьян У. В. Проверка знаний учащихся по математике – М.: Академия, 2005.

7.         Денищева Л. О., Кузнецова Л. В., Лурье И.А. и др. Зачеты в системе дифференцированного обучения математики – М: Просвещение, 2003.

9. Зив Б. Г. Задачи к урокам алгебры: 7-11 кл. – М.: Русское слово, 2003.

10. Ильина Т. А. Педагогика: курс лекций: учебное пособие для студентов пед. ин-тов.– М: Просвещение, 2004.

11. Калинина М.И. К вопросу о систематизации знаний учащихся/ сб. статей, сост. Борчугова З. Г., Батий Ю. Ю. – М.: Просвещение, 2004.

12. Колобова Е. В. Использование зачетной системы для контроля и оценки знаний учащихся // Математика в школе , 2004. - №3.

13. Качество знаний учащихся и пути его совершенствования / Под ред. Скаткина М.Н., Краевского М.Н. – М.: Педагогика, 2003.

14. О совершенствовании методов обучения математики / Сб. статей сост. Крамор В. С. – М.: Просвещение, 2004.

15. МПМ в средней школе. Частная методика / Сост. Мишин В. И. – М: Просвещение, 2003.

16. Петровский Е. И. Проверка и оценка знаний учащихся – М.: АПН РФ, 2005.

18. Планирование обязательных результатов обучения математике / сост. В. В. Фирсов – М.: Просвещение, 2002.

19. Программы общеобразовательных учреждений. Математика – М: Просвещение, 2006.

21. Скобелев Г. Н. Систематизация знаний на уроках математики – Минск, 2006.

22. Современные основы школьного курса математики. / Н. Я. Виленкин, К. И. Дудничев, Л. А. Калужнин, А. А. Столяр. – М.: Просвещение, 2004.

23. Утеева Р. А. Групповая работа как одна из форм деятельности учащихся на уроке // Математика в школе, 2005. - №2.

24. Харламов И. Ф. Педагогика. Курс лекций. – Минск, 2005.

25. Шаталов В. Ф. Куда и как исчезли тройки – М.: Педагогика, 2004.