Обязательно нужно проводить количественный и качественный анализ систематизационной работы

7.         Обязательно нужно проводить количественный и качественный анализ систематизационной работы.

Данные количественного анализа удобно представлять в виде таблицы

Но данные количественного анализа не позволяют установить уровень владения материалом конкретного ученика. Такую возможность представляет качественный анализ. Информация, которая подвергается качественному анализу, должна включать данные о выполнении каждого задания предложенной систематизационной работы каждым учеником класса. Такие данные можно фиксировать в таблице.

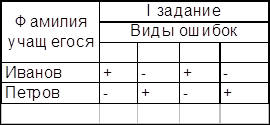
Содержание основной части таблицы свидетельствует об основных ошибках учащихся, допущенных при выполнении отдельных заданий.

Анализ результатов систематизационной работы может способствовать получению выводов об особенностях своей деятельности по организации усвоения школьниками учебного материала.

Машинные средства формы

Для систематизации знаний учащихся используют персональный компьютер. Для систематизации знаний учащихся удобно применять типовые расчеты, которые включают наиболее характерные задания базового курса математики. Перечислим некоторые преимущества использования компьютера для создания типовых расчетов:

1. Однотипные задания печатаются в любом количестве неповторяющихся вариантов;

2. Варианты, созданные с помощью компьютерных программ, проверяются значительно быстрее, так как компьютер может предоставить ответы к каждому заданию;

3. Компьютерные типовые задания удобны для отработки необходимых навыков с отстающими учащимися (учитель не тратит время на подбор однотипных заданий для отработки определенных навыков);

4.Учащиеся с огромным интересом работают с такими заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней.

Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе

 

2.1. Тематическое планирование

Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. От того, как она организована, на что нацелена, существенно зависит содержание работы на уроке, как всего класса в целом, так и отдельных учащихся. Вся система систематизации знаний и умений учащихся должна планироваться таким образом, чтобы охватывались все обязательные результаты обучения для каждого ученика. Одновременно в ходе систематизации надо дать учащимся возможность проверить себя на более высоком уровне, проверить глубину усвоения материала. В ходе изучения темы учитель проверяет результаты обучения путем проведения текущих самостоятельных работ, устного опроса, систематизационных работ и других форм систематизации.

История развития математического знания даёт возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры.

Требования к знаниям и умениям учащихся в данном курсе не завышены. Так как чрезмерность требований порождает перегрузку, что ведёт к угасанию интереса к математике. Применение компьютерной технологии (презентации, слайды, поиск информации по имеющимся источникам) заинтересовывает учащихся данным курсом, что, помогая лучше овладеть ЗУН. Курс оснащён информационно-программным средством “Этот удивительный мир чисел, электронная версия”.

Цели курса: обобщение и систематизация, расширение и углубление знаний о множестве чисел, обретение практических навыков при выполнении тренировочных заданий, привитие устойчивого интереса к математике, повышение уровня математической подготовки школьников; увеличение количества учащихся, для которых математика станет профессионально значимым предметом.

Задачи курса:

·           сформировать у учащихся логическое представление о числах; > восполнить пробелы в знаниях о числах;

·           сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;

·           сформировать навыки самостоятельной работы;

·           сформировать умения и навыки исследовательской работы, работы со справочной литературой, с компьютером;

·           способствовать развитию алгоритмического мышления, воспитанию умений действовать по данному алгоритму;

·           показать, что источник возникновения изучаемых понятий - реальный мир, что они возникли из практических потребностей людей;

·           показать, что понятия не изолированы друг от друга, а представляют определённую систему знаний, все звенья которой находятся во взаимной связи;

·           способствовать развитию творческого и логического мышления учащихся;

·           способствовать формированию познавательного и устойчивого интереса к математике;

·           пополнить исторические сведения;

·           обеспечить условия для расцвета личности школьника с учётом возрастных особенностей;

·           привить навыки работы в группах, выступать, вести переговоры, отстаивать свое мнение и интересы;

·           подготовка учащихся к профильной школе.

Календарно – тематическое планирование.

№/№	Тема занятий.	Кол - во часов.	Дата прове­дения.	Виды деятель­ности.	Обору­дование.
1.	Натуральные и целые числа.	Зч.
1	Натуральные числа. Система счисления.	1ч.		Анкетирование, аукцион знаний, демонстр. презен­тации.	Лист ответов, компьютер, программ. обес­печение.
2	1ростые и составные числа. НОД (Алгоритм Евклида).	1ч.		Исследов. работа, Работа со справоч­ником, практикум.	Компьютер, про­граммное обеспечение
3	Множество целых чисел. Самостоятельная работа.	1ч.		Беседа, работа со справочником. Самостоят. прове­рочная работа	Компьютер, про­граммное обес­печение. Лист ответов.
2.	Рациональные числа.	1ч.
1	Обыкновенные и десятичные дроби. Периодические дроби. -	1ч.		Исследов. работа. Работа со справоч­ником, практикум.	Компьютер, про­граммное обеспе-ние .
3.	Действительные числа.	Зч.
1	Непериодические бесконечные десятичные дроби. Иррациональные числа.	1ч.		1екция, аукцион знаний.	Компьютер, программное обеспечение.
2	Коредь 1с-й степени из действительного числа.	1ч.		Работа со справочником, практикум.	Компьютер, программное обесп.
3	Систематизацияное тестирование.	1ч.		Самостоятельная работа.	Компьютер, лист ответов.
4.	Комплексные числа.	Зч.
1.	Алгебраическая форма комплексного числа. Действия с комплексными числами.	1ч.		Проблемная беседа Практикум.	Компьютер, программное обссп.
2.	Применение комплексного числа.	1ч.		Лекция.	Компьютер, программное обесп.
3.	Систематизационное тестирование.	1ч.		Самостоятельная работа.	Компьютер, лисе ответов.
5.	Круглый стол	2ч.		Вопросы - ответы. Обсуждение. Анкетирование	Заготовленные вопросы. Лист ответов.
	Итого:	12ч.

Тест

Действительные числа

1. Обратить обыкновенную дробь в десятичную:

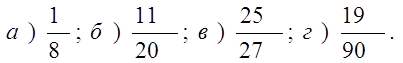
Ответ: а) 1) 0,102; 2) 0,125; 3) 0,1205.

б) 1) 0,55; 2)0,505; 3)0,255.

в) 1) 0,(925); 2) 0,9(25); 3) 0,92(5).

г) 1) 0;21; 2) 0,2(1); 3)0,(21).

2. Обратить десятичную дробь в обыкновенную:

а) 0,15; б) 0,225; в) 0,(6); г) 2,2(41).

Ответ: а) 1) 3/20; 2) 4/17; 3) 3/5.

б) 1) 9/40; 2) 2/19; 3) 1/40.

в) 1) 2/3; 2) 1/9; 3) 3/7.

г) 1) 2219/90; 2) 2219/990; 3)2219/999.

3)Выписать из данных чисел иррациональные:

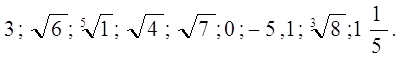
Ответ: а) 1)

2)

3)

4. При каких х имеет смысл выражение:

А.

Ответ: а) 1) х>0; 2) x<0; 3) x- любые числа.

б) 1) х>5; 2) x<5; 3) x- любые числа.

в) 1) х ≥5; 2) x≤5; 3) x- любые числа.

Б.

Ответ: а) 1) х ≥0; 2) x≤0; 3) x- любые числа.

б) 1) х ≥3; 2) x≤3; 3) x- любые числа.

5* Упростить выражение:

Б.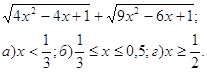

Ответ: а) 1) 2-5х; 2) 5х-2; 3) x;

б) 1) 5х-2; 2) 2-5х; 3) x;

в) 1) 2-5х; 2) x; 3) 5х-2;

В.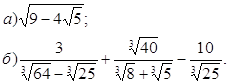

Ответ: а)

б)  

Тест

Комплексные числа.

1. Изобразить комплексные числа на координатной оси: z₁=4-6i; z₂=3+i; z₃=-5i; z₄=4-0i; z₅=-1,5=3i; z₁=-2-8i;

2. Для комплексных чисел z₁ и z₂ найти:

1)z₁+ z₂; 2)z₂- z₁; 3) z₁z₂; 4) z₁: z₂:

z₁ = 5-3i , z₂ = -4+7i.

Ответ:1. а)z₁+ z₂=1+4i_; б)z₁+ z₂ =4+i_; в)z₁+ z₂=2+3i_;

2. а)z₂- z₁=9-10i_; б) z₂- z₁=-9+10i; в)z₂- z₁= -9-10i;

3. а)z₁z₂=-41+47i; б) z₁z₂=-1-47i; в)z₁z₂=1+47i;

4. а)z₁: z₂=; б) z₁: z₂=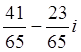; в) z₁: z₂=.

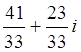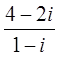3. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней

х₁ =

Ответ: а) x²-6x+10=0; б) x²-6x+8=0; в) x²+6x-10=0

4. Вычислить: 1)i²¹ ,2) i⁷⁵ ,3) i⁴⁴

Ответ: 1) а)i; б)1; в)-i;

2) а)i; б)1; в)-i;

3)а)i; б)1; в)-i.

5. Выполнить действия:

1) (2+5i)² (3-i);

2)*

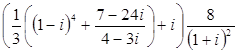
Ответ: 1. а)-43+81i_; б)-83+81i_;в)-23+39i_;

2. а)8i; б)0; в)-4i.

2.2. Планы-конспекты уроков

План-конспект №1. Тема урока: «Графический способ решения систем уравнений».

Цели урока:

·           открыть совместно с учащимися новый способ решения систем уравнений, закрепить навыки построения графиков элементарных функций;

·           формировать потребность приобретения новых знаний, создать условия для систематизации (самосистематизации) усвоения умений и навыков;

·           развивать математическую речь при комментировании решения;

·           воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, развивать самостоятельность и творчество.

Ход урока.

Для урока мы используем следующую литературу: Учебник Ю.Н. Макарычева “Алгебра 9” под редакцией С.А. Теляковского., “Сборник задач для проведения письменного экзамена по алгебре за курс основной школы” “Дрофа” Москва 2001г., Материалы Единого Государственного Экзамена.

Во время урока учащийся ведет лист самосистематизации, где в ходе урока оценивает свое участие по 3-х бальной шкале (0,1,2).

1 – Самоопределение к деятельности. Организационный момент

Эпиграф: Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю (Гёте И.)

2 – Актуализация знаний и фиксация затруднений в деятельности.

А) Какие способы решения систем уравнений вы знаете?

Б) Решить систему уравнений (любым способом)

1. 2. 3.

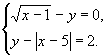
Решение системы №1:

Ответ (1,5;1,5)

Решение системы №2

Ответ (-3;2)

Решение системы 3 вызывает у учащихся затруднение. Известными способами эту систему не решить.

3 - Постановка учебной задачи.

Учащиеся формулируют цель урока: “Научиться решать системы новым способом”

Вспоминаем недавно изученный графический способ решения уравнений. Нельзя ли его применить к решению систем. Вспомните определение графика уравнения с двумя переменными.

Работа устно:

С помощью каких преобразований можно построить графики данных элементарных функций.

А)

Б)

В)

Г)

Д)

Е)

Ж)

4 – Построение проекта выхода из затруднений.

Совместное создание алгоритма решения систем:

1.         выразить переменную У через Х (если возможно);

2.         построить график каждого уравнения;

3.         найти координаты точки пересечения графиков.

Координаты любой точки построенного графика являются решением уравнения, следовательно, координаты каждой точки пересечения являются решением системы уравнений.

На доске учащиеся решают систему №3

 

 

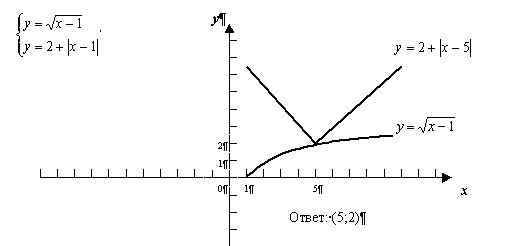
5 – Первичное закрепление (работа у доски по учебнику)

Решить графически систему уравнений

№233

Решение:

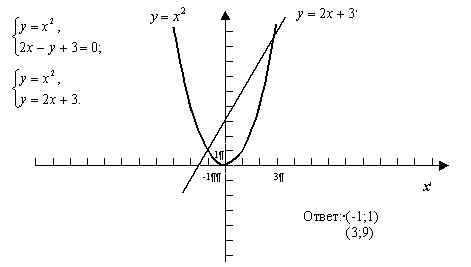
С помощью графиков решите систему уравнений

№236 а

Решение:

 

Физ. Минутка.

(ведет физорг или валеолог класса).

Самостоятельная работа с самопроверкой. По вариантам. Упражнения взяты из “Сборника заданий для проведения экзамена по алгебре за курс основной школы”

1) Решите графически систему.

1 вар. №203 2 вар. №206

2) С помощью графиков определите: сколько решений имеет система уравнений

1 вар. 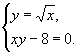2 вар.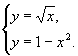

Решение №203 – 1 вариант.

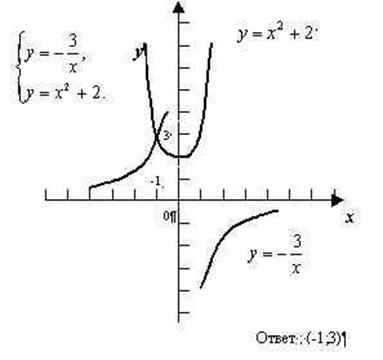
Решение №206 вариант 1

 

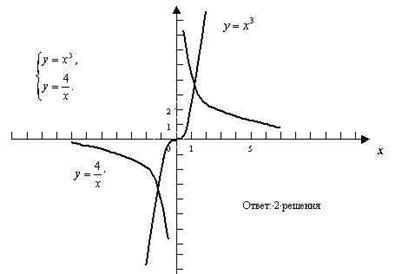
№203 вариант 2

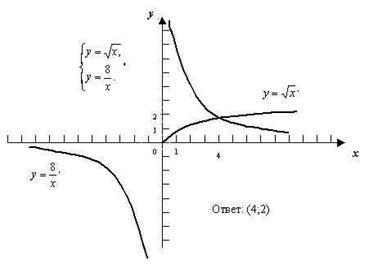
№206 вариант 2:

 

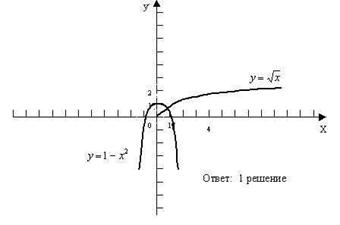
В конце работы выявляются причины ошибок или затруднений.

Работа творческого характера (по группам).

1.         Решить систему

2.         По готовому рисунку составить систему.

Учащиеся оценивают свое участие в работе групп.

 Систематизация знаний:

1.         Что нового вы узнали на уроке?

2.         Достигли ли вы, поставленной в начале урока, цели?

3.         Какую цель вы для себя ставите на следующем уроке?

В конце урока учащиеся сдают листы самооценки учителю.

Домашнее задание: № 302, № 304 или №305.

План-конспект №2. Компьютерные технологии на уроке математики в 9-м классе

Из классической педагогической литературы известно, что наиболее эффективной является такая организация учебного процесса, при которой максимально стимулируются творческие способности учащихся, и используются возможности новых информационных технологий обучения в организации внутреннего диалога учащихся на основе мультимодального взаимодействия.

Урок проходит в кабинете математики, оборудованном компьютерами, связанными локальной сетью в 9 классе с углубленным изучением математики, в котором учащиеся занимаются по подгруппам.

Тема: Метод замены переменной в уравнениях. Исследование структуры уравнений приводимых к квадратным. (2 часа).

1-й час – исследование уравнений высших степеней, имеющих более сложную структуру, чем те, которые изучались в восьмом классе.

2-й час – урок-практикум - решения задач.

Цели:

1) выработать умение учащихся видеть структуру уравнений и выбирать наиболее эффективно замену переменных для их решения на основе анализа коэффициентов уравнения;

2) расширить круг приемов решения уравнений, приводимых к квадратным;

3) углубить теоретические основы подхода к решению уравнений;

4) развить навыки работы с информационными технологиями;

5) активизировать интеллектуальную деятельность учащихся.

Задачи:

1) распознавание уравнений, приводимых к квадратным;

2) обоснование выбора подходящей замены переменных;

3) отработка навыков решения подобных уравнений;

4) повторение способов решения различных типов уравнений, сводящихся к квадратным;

5) развитие умения самостоятельно осуществлять небольшие исследования;

6) тренировка умения работы с электронными учебно-методическими материалами.

Схема урока.

I. Повторение пройденного материала и вопросов, подготавливающих к пониманию новых задач.

II.

1) Методы решения квадратных уравнений:

а) формула корней квадратного трехчлена;

б) выделение полного квадрата;

в) использование теоремы, обратной теореме Виета;

г) разложение на множители;

2) теоретические положения о количестве корней квадратного трехчлена;

3) теоремы о тождественных преобразованиях и равносильности уравнений;

4) метод замены переменной в биквадратных уравнениях.

Форма проведения урока – сочетание объяснения учителя с фронтальной коллективной работой учащихся.

III. Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения.

Исследование структуры и решение уравнений, сводящихся к квадратным, на следующих примерах:

Объяснение учителя.

1) ;

2) ;

3) .

Далее №№9.15(а); 9.16(а); 923(а) - решаются учащимися на доске.

Применение учащимися приобретенных знаний в самостоятельном выполнении задания по выбору подходящей замены переменной в решении уравнений, приводимые к квадратным.

Каждый ученик имеет свое рабочее место за персональным компьютером, на котором он получает свой вариант задания, сгенерированный компьютером по числу учеников по образцу подобранному учителем, решает и вводит с клавиатуры свой ответ.

Систематизация и обобщение знаний: После окончания выполнения задания компьютер проверяет ответ и выставляет оценку. В случае удовлетворительной (или неудовлетворительной) оценки ученик имеет возможность изучить правильное решение, запросив на компьютере соответствующую опцию, просмотреть правильное решение и выявить допущенные ошибки. Полученные оценки выставляются учителем в журнал.

IV. Образец вариант задания, получаемого учащимися на этом уроке:

1) ;

2) ;

3) .

Домашнее задание: №№ 9.14(в, г), 9.16(б, г), 9.23(в, г).

М.А. Галицкий, А.М. Гольдман, Л.И. Звавич “Сборник задач по алгебре” 8 – 9 класс.