Навигация
Интерполяция функции одной переменной методом Ньютона
23209
знаков
3
таблицы
3
изображения
Аннотация
Пояснительная записка курсовой работы "Интерполяция функции одной переменной методом Ньютона" содержит в себе введение, анализ задания описанием входных и выходных данных, обзор литературных источников, описание математической модели и методов вычислительной математики, пояснения к алгоритму, текст программы, инструкцию. При изучении дисциплины "Информатика" для написания курсовой работы использовались различные литературные источники, которые перечислены в настоящем документе. В данной курсовой работе приведена программа, которая применяется для интерполяции таблично заданной функции методом Ньютона. В ней был использован метод структурного программирования для облегчения написания и отладки программы, а также повышения ее наглядности и читаемости. Целью написания данной работы было получение и закрепление практических навыков разработки алгоритмов различными методами. Представленная программа реализована на языке программирования Pascal. Пояснительная записка содержит 25 листов, на которых размещено два рисунка, текст программы и описание программы и алгоритма.
Содержание
Введение
Анализ задания
Математическая модель задачи
Программирование функции формулы Ньютона
Обзор литературных источников
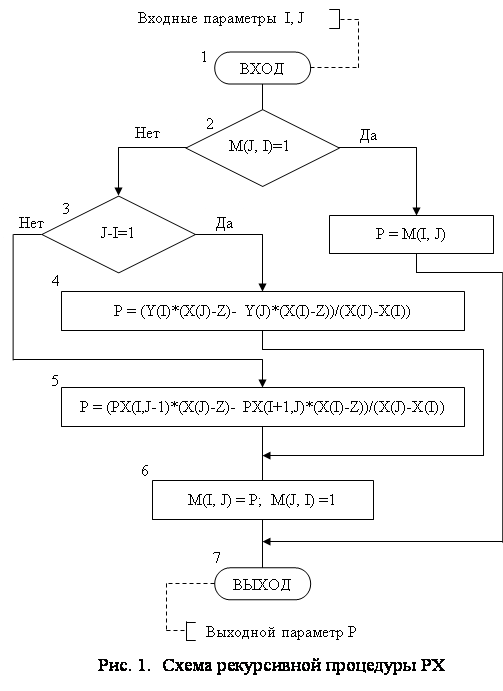
Разработка программы по схеме алгоритма
Инструкция пользования программой
Текст программы
Исходные данные и результат решения контрольного примера
Заключение
Список использованных источников
Введение
Современное развитие физики и техники тесно связано с использованием электронных вычислительных машин (ЭВМ). В настоящее время ЭВМ стали обычным оборудованием многих институтов и конструкторских бюро. Это позволило от простейших расчетов и оценок различных конструкций или процессов перейти к новой стадии работы - детальному математическому моделированию (вычислительному эксперименту), которое существенно сокращает потребность в натурных экспериментах, а в ряде случаев может их заменить.
Сложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных -таких как вычисление интеграла, решение дифференциального уравнения и т. п. Многие элементарные задачи являются несложными и хорошо изучены. Для этих задач уже разработаны методы численного решения, и нередко имеются стандартные программы решения их на ЭВМ. Есть и достаточно сложные элементарные задачи; методы решения таких задач сейчас интенсивно разрабатываются.
В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ.
Анализ задания
В качестве входных данных использованы:
1. Количество узлов.
2. Табличные значения функции.
Выходными данными, т.е. результатом программы является:
1. Значения таблично заданной функции в промежуточных значениях.
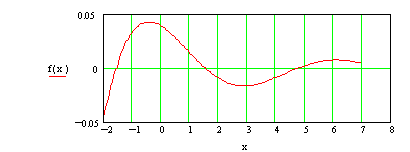
2. График полинома.
Математическая модель задачи
При выполнении курсовой работы была выбрана следующая математическая модель:
Интерполяция и приближение функций.
1. Постановка задачи.
Одной из основных задач численного анализа является задача об интерполяции функций. Часто требуется восстановить функцию 
для всех значений 
на отрезке 
если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислении) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.
Пусть и» отрезке задана сетка со
и в ее узлах заданы значения функции 
, равные
.
Требуется построить интерполянту — функцию , совпадающую с функцией в узлах сетки:
.
Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений для значений , не содержащихся в таблице данных.
Похожие работы
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
x, отличных от узлов интерполяции. Такая операция называется интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда x принадлежит интервалу [x0, xn], и экстраполирование, когда x не принадлежит этому интервалу. В такой общей постановке задача интерполирования может иметь бесчисленное множество решений. Чтобы получить единственную функцию F(x), необходимо ...
... корни находятся на расстоянии b: . Тогда , откуда Знак перед корнем выбирают с таким расчетом, чтобы получить наибольшее значение знаменателя. Еще один метод, который применяют для поиска корней полиномов, – метод сопровождающей матрицы (companion matrix). Можно доказать, что матрица , называемая сопровождающей матрицей для полинома , имеет собственные значения равные корням полинома ...
... звеньев первого и второго порядка представлена на следующем рисунке: 3. Методы расчета БИХ-фильтров и вид целевой функции Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях. ...
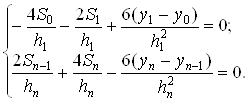
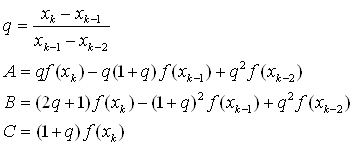
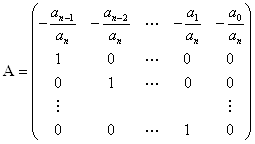
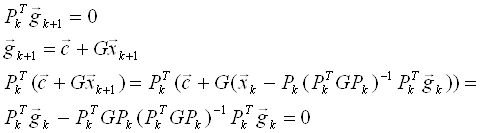
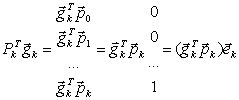
0 комментариев