Навигация
Градиентный метод с дроблением шага
2.2 Градиентный метод с дроблением шага
Большей эффективностью обладают итерационные процедуры, в которых приближение к минимуму осуществляется сразу по всем переменным. При этом задача состоит в нахождении последовательности векторов ![]() таких, что
таких, что
![]() (2.2)
(2.2)
Методы построения таких последовательностей называют методами спуска. Пусть ![]() Поставим задачу отыскания последовательности
Поставим задачу отыскания последовательности ![]() ., сходящейся к
., сходящейся к ![]() .
.
Выберем произвольным образом точку ![]() , направление
, направление ![]() и сконструируем луч
и сконструируем луч
![]() . (2.3)
. (2.3)
Рассмотрим вопрос о выборе направления ![]() , обеспечивающего (2.2). Для этого изучим поведение
, обеспечивающего (2.2). Для этого изучим поведение ![]() вдоль луча
вдоль луча ![]() . Имеем
. Имеем ![]()
Введем
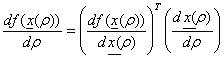 (2.4)
(2.4)
Здесь ![]()
В соответствии с (2.3)
![]()
Тогда ![]()
Вычислим 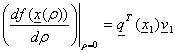 (2.5)
(2.5)
Теперь, чтобы для любого ![]() обеспечить отрицательность (2.5), достаточно положить
обеспечить отрицательность (2.5), достаточно положить ![]() , где
, где ![]() произвольная положительно определенная
произвольная положительно определенная ![]() матрица. Тогда
матрица. Тогда
![]()
При этом ![]() (2.6)
(2.6)
Выбрав каким-либо образом ![]() , получим
, получим ![]() Затем аналогично рассчитаем
Затем аналогично рассчитаем ![]()
Общее рекуррентное соотношение имеет вид :
![]() (2.7)
(2.7)
Различные варианты градиентных процедур отличаются друг от друга способом выбора ![]() .
.
Полученное соотношение (2.7) обеспечивает построение последовательности точек ![]() , сходящейся к точке
, сходящейся к точке ![]() , минимизирующей
, минимизирующей ![]() . Понятно, что каждая из точек этой последовательности может рассматриваться как некоторое приближение к точке минимума
. Понятно, что каждая из точек этой последовательности может рассматриваться как некоторое приближение к точке минимума ![]() , положение которого, вообще говоря, остается неизвестным в ходе всей процедуры спуска. Поэтому для всех таких процедур принципиальной остается проблема останова. В вычислительной практике часто используются следующие критерии останова:
, положение которого, вообще говоря, остается неизвестным в ходе всей процедуры спуска. Поэтому для всех таких процедур принципиальной остается проблема останова. В вычислительной практике часто используются следующие критерии останова:
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
где ![]() и
и ![]() -некоторые достаточно малые числа .
-некоторые достаточно малые числа .
Понятно, что критерий (2.8) хорош в тех случаях, когда функция ![]() в окрестности минимума, используя ранее введенную классификацию, имеет характер «глубокой» впадины. С другой стороны, если функция
в окрестности минимума, используя ранее введенную классификацию, имеет характер «глубокой» впадины. С другой стороны, если функция ![]() ведет себя как «пологое плато», то более предпочтительным является критерий (2.9). Аналогом критерия (2.8) является другое часто применяемое правило останова :
ведет себя как «пологое плато», то более предпочтительным является критерий (2.9). Аналогом критерия (2.8) является другое часто применяемое правило останова :
![]() , (2.10)
, (2.10)
использующее необходимое условие экстремума функции. Очевидным недостатком критериев (2.8)-(2.10) является то, что их качество существенно зависит от абсолютных значений величины ![]() и компонентов векторов
и компонентов векторов ![]() ,
,![]() . Более универсальными являются относительные критерии :
. Более универсальными являются относительные критерии :
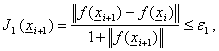 (2.11)
(2.11)
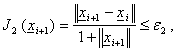 (2.12)
(2.12)
 (2.13)
(2.13)
Заметим, что очень часто на практике используются составные критерии, представляющие собой линейную комбинацию критериев (2.11)-(2.13), например,
![]()
![]()
Иногда применяют другой вариант построения составного критерия :
![]()
При реализации градиентного метода с дроблением шага в качестве ![]() выбирают единичную матрицу, то есть
выбирают единичную матрицу, то есть
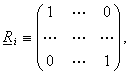
а длину шага определяют путем проверки некоторого неравенства. При этом основное рекуррентное соотношение (2.7) приобретает вид :
![]()
Ясно, то если ![]() , выбирать достаточно малым, то это обеспечит убывание
, выбирать достаточно малым, то это обеспечит убывание ![]() , но потребуется весьма большое число шагов. Если же неосторожно выбрать
, но потребуется весьма большое число шагов. Если же неосторожно выбрать ![]() большим , то можно проскочить минимум, а это опасно в связи с возможным осциллированием. Для выбора шага используется правило Голдстейна-Армийо :
большим , то можно проскочить минимум, а это опасно в связи с возможным осциллированием. Для выбора шага используется правило Голдстейна-Армийо :
а) ![]() (2.14)
(2.14)
б) ![]() (2.15)
(2.15)
Выполнение условия а) обеспечивает выбор ![]() не слишком большим. Выполнение условия б) не дает возможность выбрать
не слишком большим. Выполнение условия б) не дает возможность выбрать ![]() слишком малым.
слишком малым.
Практическая процедура строится следующим образом. Выбирается начальная точка ![]() и некоторое начальное значение
и некоторое начальное значение ![]() , проверяется (2.14) и, если оно выполняется, то делается шаг в направлении
, проверяется (2.14) и, если оно выполняется, то делается шаг в направлении ![]() В новой точке
В новой точке ![]() вычисляется градиент
вычисляется градиент ![]() и вновь проверяется условие (2.14). В случае его удовлетворения продвижение к минимуму продолжается с тем же шагом. Если же оно не удовлетворяется, то параметр
и вновь проверяется условие (2.14). В случае его удовлетворения продвижение к минимуму продолжается с тем же шагом. Если же оно не удовлетворяется, то параметр ![]() , определяющий длину шага, делят пополам до тех пор, пока это неравенство не будет выполнено. Затем выполняется очередной шаг. Процедура продолжается до выполнения критерия останова.
, определяющий длину шага, делят пополам до тех пор, пока это неравенство не будет выполнено. Затем выполняется очередной шаг. Процедура продолжается до выполнения критерия останова.
Похожие работы
... практичных алгоритмов оптимизированного перебора, позволяющих за разумное время осуществлять распараллеливание достаточно больших участков. Анализ работ, посвященных оптимизации кода для процессоров с параллелизмом на уровне команд показывает, что для достижения наилучших результатов необходимо применение комплекса оптимизаций, среди которых можно выделить следующие классы. Преобразования циклов ...
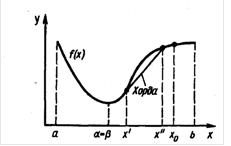
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
... переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: · рационального использования сырья и материалов; задачи оптимизации раскроя; · оптимизации производственной программы ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...


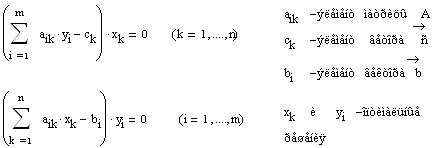
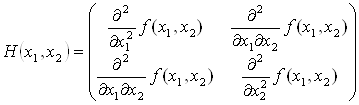

0 комментариев