Моделирование движения на плоскости

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Теория механизмов и машин» Моделирование движения на плоскости КУРСОВАЯ РАБОТА

по курсу «Информатика»

Исполнитель Лабоцкий Д.В.

2006

Содержание

Введение

1.   Постановка задачи

2.   Математическая модель объекта или процесса

3.   Алгоритм решения задачи

4.   Схема алгоритма решения задачи

5.   Таблица идентификаторов

6.   Текст программы

7.   Распечатка результатов

8.   Графическое представление результатов

9.   Анализ результатов

Литература

Введение

Современная технология изготовления разнообразных конструкций, механизмов, машин предполагает обязательное проведение точных расчетов, моделирования и испытания моделей. Для использования всевозможных процессов и явлений в эксплуатационных целях необходимо предоставить расчет их параметров и характеристик. В процессе обработки или сборки деталей приходится перемещать их на определенные расстояния. Для обеспечения точности и производительности, минимальных затрат энергии и ресурсов целесообразно применять автоматизированные системы.

1.         Постановка задачи

Вал с моментом инерции I0=2,5 кг·м2, на который действует момент движущих сил

Md=M0+ln(φ+1)+

где М0=15,5 Нм, и момент сил сопротивления Мс=10 Нм, разгоняется при повороте на угол φр=0,2 рад/с, n=8. После этого действие движущего момента прекращается (момент Мс продолжает действовать), начинается торможение, в процессе которого вал повернется до остановки на угол φt за счет накопленной при разгоне кинетической энергии.

Требуется:

-           определить зависимости от угла поворота φ скорости ω(φ), ускорения ε(φ), времени t(φ);

-           установить время Тр поворота на угол φр и время Тt поворота на угол φt;

-           по полученным данным построить графики ω(φ), ε(φ), t(φ) для интервала угла поворота [0, φр+φt].

При вычислении зависимости ω, ε, t от угла поворота будет получена табличная зависимость, при этом учтем, что зависимость времени от угла поворота, является функцией монотонно возрастающей.

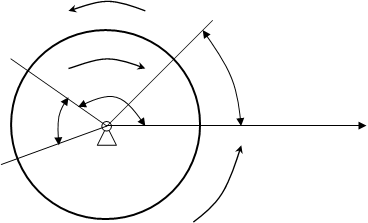Мd

Mc

φp  φ

φt

Схема, поясняющая словесную постановку задачи для определения параметров движения при вращательном движении.

2.         Математическая модель объекта

Анализ вращательного движения тела показывает, что исходными данными для определения параметров движения (перемещения, скорости, ускорения, времени) являются моменты инерции (I0), движущие моменты (Мd), и моменты сопротивления (Мс), а также начальные значения параметров движения.

При использовании дискретной модели задачи весь путь разбивается на некоторое количество элементарных участков длиной Δφ=φi-φi-1.

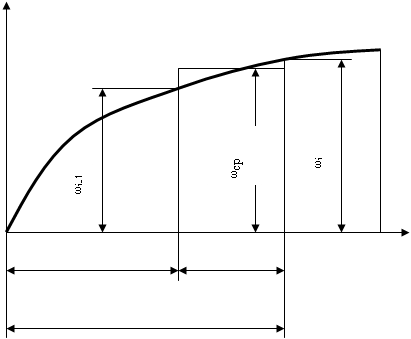
V

φi-1 Δφ φ

φi

На каждом интервале связь кинематических, силовых и массовых параметров описывается теоремой об изменении кинетической энергии, в частности:

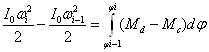
откуда можно выразить скорость движения:

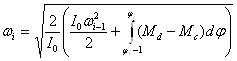
При определении времени Δt прохождения участка Δφ будем считать скорость движения постоянной, равной средней скорости в пределах участка:

 

Тогда Δt=ti-ti-1=,

откуда ti=ti-1+ или ti=ti-1+

Аналогично, предполагая, что ускорение ε i на участке Δφ постоянно, имеем:

ε i= ε cp=

Применим построенную математическую модель к расчету параметров вращательного движения тела на участке разгона [0, φp] и на участке торможения [φp, φp+φt].