Навигация
Если каждое из них имеет одно и то же множество имен атрибутов (следовательно, заметьте, они заведомо должны иметь одну и ту же степень);
1. если каждое из них имеет одно и то же множество имен атрибутов (следовательно, заметьте, они заведомо должны иметь одну и ту же степень);
2. если соответствующие атрибуты (т.е. атрибуты с теми же самыми именами в двух отношениях) определены на одном и том же домене.
Операции объединения, пересечения и вычитания требуют от операндов совместимости по типу.
Объединением двух совместимых по типу отношений А и В (A UNION B) называется отношение с тем же заголовком, как и в отношениях А и В, и с телом, состоящим из множества всех кортежей, принадлежащих А или В или обоим отношениям.
Пример операции объединения отношений приведен на рис. 4.1 – рис. 4.2.
| A | B | |||||
| CityNo | CityName | RgNo | CityNo | CityName | RgNo | |
| 1 | Желтые Воды | 1 | 2 | Кривой Рог | 1 | |
| 2 | Кривой Рог | 1 | 3 | Пятихатки | 1 | |
| 3 | Пятихатки | 1 | 4 | Львов | 2 | |
рис. 4.1 Исходные отношения
| A UNION B | ||
| CityNo | CityName | RgNo |
| 1 | Желтые Воды | 1 |
| 2 | Кривой Рог | 1 |
| 3 | Пятихатки | 1 |
| 4 | Львов | 2 |
рис. 4.2 Результат объединения отношений A и B.
4.3.2 ПересечениеПересечением двух совместимых по типу отношений А и В (A INTERSECT B) называется отношение с тем же заголовком, как и в отношениях А и В, и с телом, состоящим из множества всех кортежей, принадлежащих одновременно обоим отношениям A и B.
Пример операции пересечения отношений приведен на рис. 4.1 и рис. 4.3.
| A INTERSECT B | ||
| CityNo | CityName | RgNo |
| 2 | Кривой Рог | 1 |
| 3 | Пятихатки | 1 |
рис. 4.3 Результат операции пересечения отношений A и B.
4.3.3 ВычитаниеВычитанием двух совместимых по типу отношений А и В (A MINUS B) называется отношение с тем же заголовком, как и в отношениях А и В, и с телом, состоящим из множества всех кортежей, принадлежащих отношению A и не принадлежащих отношению B.
Пример операции вычитания отношений приведен на рис. 4.1 и рис. 4.4.
| A MINUS B | B MINUS A | |||||
| CityNo | CityName | RgNo | CityNo | CityName | RgNo | |
| 1 | Желтые Воды | 1 | 4 | Львов | 2 | |
рис. 4.4 Результат операции вычитания отношений A минус B и B минус A.
4.3.4 ПроизведениеВ математике декартово произведение (или для краткости произведение) двух множеств является множеством всех таких упорядоченных пар элементов, что первый элемент в каждой паре берется из первого множества, а второй элемент в каждой паре берется из второго множества. Следовательно, декартово произведение двух отношений, должно быть множеством упорядоченных пар кортежей. Но опять-таки необходимо сохранить свойство замкнутости; иначе говоря, результат должен содержать кортежи, а не упорядоченные пары кортежей.
Декартово произведение двух отношений А и В (A TIMES B), где А и В не имеют общих имен атрибутов, определяется как отношение с заголовком, который представляет собой сцепление двух заголовков исходных отношений А и В, и телом, состоящим из множества всех кортежей t, таких, что t представляет собой сцепление кортежа a, принадлежащего отношению А, и кортежа b, принадлежащего отношению В. Кардинальное число результата равняется произведению кардинальных чисел исходных отношений А и В, а степень равняется сумме их степеней. Пример операции декартова произведения представлена на рис. 4.5
| A | B | ||||
| CityNo | CityName | A_RgNo | B_RgNo | RgName | |
| 1 | Желтые Воды | 1 | 1 | Днепропетровская | |
| 2 | Кривой Рог | 1 | 2 | Львовская | |
| 3 | Пятихатки | 1 | |||
| A TIMES B | ||||
| CityNo | CityName | A_RgNo | B_RgNo | RgName |
| 1 | Желтые Воды | 1 | 1 | Днепропетровская |
| 1 | Желтые Воды | 1 | 2 | Львовская |
| 2 | Кривой Рог | 1 | 1 | Днепропетровская |
| 2 | Кривой Рог | 1 | 2 | Львовская |
| 3 | Пятихатки | 1 | 1 | Днепропетровская |
| 3 | Пятихатки | 1 | 2 | Львовская |
рис. 4.5 Результат операции декартово произведение отношений A и B.
Явное использование операции декартова произведения требуется только для очень сложных запросов. Эта операция включена в реляционную алгебру главным образом по концептуальным соображениям. Декартово произведение требуется как промежуточный шаг при определении операции Q-соединения которая используется довольно часто.
4.4 Свойства основных операций реляционной алгебрыОперации объединения, пересечения и декартова произведения (но не вычитания) обладают свойствами ассоциативности и коммутативности.
Пусть А, В и С – произвольные реляционные выражения (дающие совместимые по типу отношения). Тогда операция объединения:
(A UNION В) UNION С
Эквивалентна операции:
А UNION (В UNION С) (свойство ассоциативности), а .операция объединения:
А UNION B эквивалентна операции:
В UNION A (свойство коммутативности). Аналогично свойства ассоциативности и коммутативности определяются для остальных операций.
Свойство ассоциативности позволяет записывать последовательные операторы объединения (пересечения и декартова произведения) без использования круглых скобок; таким образом, выражение из предыдущего примера можно однозначно упростить:
A UNION В UNION С.
4.5 Специальные реляционные операции4.5.1 Выборка
Выборка – это сокращенное название Q-выборки, где Q обозначает любой скалярный оператор сравнения (=, ¹, >, ³, ≤, <). Q-выборкой из отношения A по атрибутам Х и Y (в этом порядке)
A WHERE X Q Y называется отношение, имеющее тот же заголовок, что и отношение А, и тело, содержащее множество всех кортежей отношения А, для которых проверка условия X Q Y дает значение истина. Атрибуты X и Y должны быть определены на одном и том же домене, а оператор должен иметь смысл для этого домена.
На рис. 4.6приведен пример операции выборки.
| A | ||
| CityNo | CityName | RgNo |
| 1 | Желтые Воды | 1 |
| 2 | Кривой Рог | 1 |
| 3 | Пятихатки | 1 |
| 4 | Львов | 2 |
| A WHERE RgNo = 1 | ||
| CityNo | CityName | RgNo |
| 1 | Желтые Воды | 1 |
| 2 | Кривой Рог | 1 |
| 3 | Пятихатки | 1 |
рис. 4.6 Исходное отношение A и результат операции выборки кортежей из отношения A по условию RGNo = 1.
4.5.2 ПроекцияПроекцией отношения А по атрибутам X, Y,..., Z, где каждый из атрибутов принадлежит отношению А
A [ X, Y, …, Z ] называется отношение с заголовком {X, Y,..., Z} и телом, содержащим множество всех кортежей {Х:х, Y:y,..., Z:z}, таких, для которых в отношении А значение атрибута Х равно х, атрибута Y равно y, ..., атрибута Z равно z.
Таким образом, с помощью оператора проекции получено "вертикальное" подмножество данного отношения, т.е. подмножество, получаемое исключением всех атрибутов, не указанных в списке атрибутов, и последующим исключением дублирующих кортежей (рис. 4.7).
A
| CityNo | CityName | RgNo |
| 1 | Желтые Воды | 1 |
| 2 | Кривой Рог | 1 |
| 3 | Пятихатки | 1 |
| 4 | Львов | 2 |
A [CityName]
| CityName |
| Желтые Воды |
| Кривой Рог |
| Пятихатки |
| Львов |
рис. 4.7 Исходное отношение A и результат операции проекции отношения A по атрибуту CityName.
Никакой атрибут не может быть указан в списке атрибутов более одного раза. Синтаксис позволяет опустить список атрибутов совсем (вместе с квадратными скобками). Действие такой операции эквивалентно указанию списка всех атрибутов исходного отношения, т.е. такая операция представляет собой тождественную проекцию. Другими словами, имя отношения является допустимым реляционным выражением. Проекция вида R[ ], т.е. такая, в которой список атрибутов не пропущен, но пустой, тоже допустима. Она представляет собой "нулевую" проекцию.
4.5.3 Естественное соединениеОперация соединения имеет несколько разновидностей. Однако наиболее важным, без сомнения, является естественное соединение, причем настолько, что для обозначения исключительно естественного соединения почти постоянно используется общий термин "соединение".
Пусть отношения А и В имеют заголовки {Xl, X2, ..., Xm, Y1, Y2, ..., Yn} и {Yl, Y2, ..., Yn, Zl, Z2, ..., Zp} соответственно; т.е. атрибуты Yl, Y2, ..., Yn (и только они) ‑ общие для двух отношений; Х1, Х2, ... ,Хm – остальные атрибуты отношения A; Zl, Z2, ..., Zp ‑ остальные атрибуты отношения В. Предположим также, что соответствующие атрибуты (т.е. атрибуты с одинаковыми именами) определены на одном и том же домене. Рассматривать выражения {X1, Х2, ..., Хm}, {Y1, Y2, ..., Yn} и {Zl, Z2, ..., Zp} как три составных атрибута X, Y и Z соответственно. Тогда естественным соединением отношений А и В (A JOIN B) называется отношение с заголовком {X, Y, Z} и телом, содержащим множество всех кортежей {Х:х, Y:y, Z:z}, таких, для которых в отношении А значение атрибута X равно х, а атрибута Y равно у, и в отношении В значение атрибута Y равно у, а атрибута Z равно z.
Пример операции естественного соединения приведен на рис. 4.8.
| A | B | ||||
| CityNo | CityName | RgNo | RgNo | RgName | |
| 1 | Желтые Воды | 1 | 1 | Днепропетровская | |
| 2 | Кривой Рог | 1 | 2 | Львовская | |
| 3 | Пятихатки | 1 | |||
| A JOIN B | |||
| CityNo | CityName | A_RgNo | RgName |
| 1 | Желтые Воды | 1 | Днепропетровская |
| 2 | Кривой Рог | 1 | Днепропетровская |
| 3 | Пятихатки | 1 | Днепропетровская |
рис. 4.8 Исходные отношения A и B и результат операции естественного соединения.
Соединение обладает свойствами ассоциативности и коммутативности. Отсюда следует, что выражения:
(A JOIN В) JOIN С и
A JOIN (В JOIN С) могут быть однозначно упрощены к следующему:
A JOIN В JOIN С
Кроме того, выражения:
A JOIN Ви
В JOIN A эквивалентны.
4.5.4 Q-соединениеОперация Q-соединения предназначается для тех случаев (сравнительно редких, но, тем не менее, встречающихся), когда нам нужно соединить вместе два отношения на основе некоторых условий, отличных от эквивалентности. Пусть отношения А и В не имеют общих имен атрибутов (как и в рассмотренной выше операции декартова произведения) и Q определяется так же, как и в операции выборки. Тогда Q-соединением отношения А по атрибуту Х с отношением В по атрибуту Y называется результат вычисления выражения
(A TIMES В) WHERE X Q Y
Q-соединение, таким образом, это отношение с тем же заголовком, что и при декартовом произведении отношений A и B, и с телом, содержащим множество кортежей, принадлежащих этому декартову произведению и вычисление условия XQY дает значение истина для этого кортежа. Атрибуты Х и У должны быть определены на одном и том же домене, а операция должна иметь смысл для этого домена.
4.5.5 ДелениеПусть отношения А и В имеют заголовки:
{X1, X2,..., Xm, Y1, Y2, ..., Yn} и {Y1, Y2, ..., Yn} соответственно, т.е. атрибуты Y1, Y2,..., Yn — общие для двух отношений, и отношение A имеет дополнительные атрибуты X1, Х2, ... ,Хm, а отношение В не имеет дополнительных атрибутов. (Отношения А и В представляют соответственно делимое и делитель.) Предположим также, что соответствующие атрибуты (т.е. атрибуты с одинаковыми именами) определены на одном и том же домене. Пусть теперь выражения {X1, Х2, ..., Хm} и {Y1, Y2, ..., Yn} обозначают два составных атрибута Х и Y соответственно. Тогда делением отношений А на В (A DIVIDEBY B) называется отношение с заголовком {X} и телом, содержащим множество всех кортежей {X:x}, таких что существует кортеж {Х:х, Y:y}, который принадлежит отношению A для всех кортежей {Y:y}, принадлежащих отношению В. Нестрого это можно сформулировать так: результат содержит такие X-значения из отношения А, для которых соответствующие Y-значения (из А) включают все Y-значения из отношения В.
Пример операции деления приведен на рис. 4.9. Отношение M является проекцией отношения Marks, а отношение S – проекцией отношения Subjects. Результат операции деления M DIVIDE BY S фактически содержит номера студентов, которые сдавали дисциплины с номерами 1 и 5.
| M | S | |||
| StNo | SubjNo | SubjNo | ||
| 1 | 1 | 1 | ||
| 1 | 5 | 5 | ||
| 2 | 1 | |||
| 2 | 5 | |||
| 3 | 1 | |||
| 3 | 5 | |||
| 4 | 1 | |||
| 5 | 1 | |||
| M DIVIDE BY S | ||||
| StNo | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
рис. 4.9. Пример операции деления.
Восемь операторов Кодда не представляют минимального набора операторов, так как не все из них примитивны, их можно определить в терминах других операторов. Например, естественное соединение – это проекция выборки произведения. Фактически три операции из этого набора, а именно соединение, пересечение и деление, можно определить через остальные пять. Операции выборки, проекции, произведения, объединения и вычитания можно рассматривать как примитивные в том смысле, что ни одна из них не выражается через другие. Поэтому минимальный набор будет состоять из этих пяти примитивных операций. Однако на практике другие три операции (в особенности соединение) настолько часто используются, что имеет смысл обеспечить их непосредственную поддержку, несмотря на то что они не примитивны.
Многие авторы предлагали новые алгебраические операторы после определения Коддом первоначальных восьми. Рассмотрим два таких оператора – EXTEND (расширение) и SUMMARIZE (подведение итогов), которые удачно дополняют основной набор восьми операторов.
4.5.6 Операция расширенияС помощью операции расширения из определенного отношения создается новое отношение (по крайней мере концептуально), которое похоже на начальное, но содержит дополнительный атрибут, значения которого получены посредством некоторых скалярных вычислений. На рис. 4.10 показаны исходное отношение и результат операции расширения:
EXTEND GROUPS ADD (2002-EnterYear) AS COURCE
| GROUPS | Результат операции расширения | ||||||
| GrNo | EnterYear | GrName | GrNo | EnterYear | GrName | Cource | |
| 1 | 1998 | А–98–51 | 1 | 1998 | А–98–51 | 2 | |
| 2 | 1999 | Б–99–51 | 2 | 1999 | Б–99–51 | 1 | |
| 3 | 1998 | Б–98–51 | 3 | 1998 | Б–98–51 | 2 | |
рис. 4.10 Пример выполнения операции расширения.
4.5.7 Операция подведения итоговПусть А1,А2,... ,An – отдельные атрибуты отношения А. Результатом операции подведения итогов
SUMMARIZE A BY (A1, A2, … An) ADD exp AS Z (которая является выражением, а не командой или оператором) будет отношение с заголовком {А1, А2, ..., An, Z} и с телом, содержащим все такие кортежи, которые являются кортежами проекции отношения А по атрибутам Al, A2, ..., An, расширенного значением для нового атрибута Z. Новое значение Z подсчитывается вычислением итогового выражения ехр по всем кортежам отношения А, которые имеют те же самые значения для атрибутов А1, А2, ..., Аn, что и кортеж t. Список атрибутов А1, А2, ..., Аn не должен включать атрибут с именем Z, а выражение ехр не должно ссылаться на атрибут Z. Кардинальное число результата равно кардинальному числу проекции отношения А по атрибутам Al, A2, ..., An, а степень результата равна степени такой проекции плюс единица.
4.5.8 Операторы обновленияРеляционная модель (точнее, ее часть, связанная с операторами) кроме реляционной алгебры может включать также операции реляционного присвоения. Такие операции имеют следующий синтаксис:
TARGET := SOURCE где source и target— реляционные выражения, представляющие совместимые по типу отношения. Вычисленное значение source присваивается отношению target, заменяя его старое значение.
В реляционных системах также существуют операции вставки INSERT, удаления DELETE и модификации UPDATE.
Оператор вставки имеет следующий вид:
INSERT source INTO target где source и target – это реляционные выражения, представляющие совместимые по типу отношения (на практике отношение target является просто именованным отношением). Значение отношения source вычисляется, и все кортежи результата вставляются в отношение target.
Оператор обновления имеет следующий вид:
UPDATE target attribute1:=scalar_expression, attribute2:=scalar_expression, …, attributeN:=scalar_expression
где target – реляционное выражение, а каждый атрибут attribute принадлежит отношению, которое является результатом вычисления указанного выражения. Все кортежи в результирующем отношении обновляются в соответствии с указанными операторами attribute2:=scalar‑expression
На практике выражение target часто будет просто ограничивающим условием для некоторого именованного отношения.
Оператор удаления имеет следующий вид:
DELETE target
где target – реляционное выражение; все кортежи в результирующем отношении удаляются.
Как и в случае с оператором обновления, выражение target часто будет просто ограничивающим условием для некоторого именованного отношения.
4.5.9 Реляционные сравненияРеляционное сравнение имеет следующий вид:
Expression Q expression где expression –это выражения реляционной алгебры, представляющие совместимые по типу отношения, а Q – один из следующих операторов сравнения:
= (равно)
¹ (не равно)
£ (подмножество)
< (собственное подмножество)
³ (надмножество)
> (собственное надмножество).
Литература:
1. Дейт К.Дж. Введение в системы баз данных. –Пер. с англ. –6-е изд. –К. Диалектика, 1998. Стр. 135–171.
ЛЕКЦИЯ 5. Вопросы проектирования БД5.1 Понятие проектирования БД
5.2 Функциональные зависимости
5.3 Тривиальные и нетривиальные зависимости
5.4 Замыкание множества зависимостей и правила вывода Армстронга
5.5 Неприводимое множество зависимостей
5.6 Нормальные формы – основные понятия
5.7 Декомпозиция без потерь и функциональные зависимости
5.8 Диаграммы функциональных зависимостей
5.1 Понятие проектирования БД
В этой лекции речь пойдет о проектировании реляционной базы данных. В общем проблема формулируется следующим образом: как в некоторой базе данных для заданного набора данных выбрать подходящую логическую структуру? Иначе говоря, нужно решить вопрос, какие базовые отношения и с какими атрибутами следует задать.
Следует отметить следующие особенности.
Похожие работы
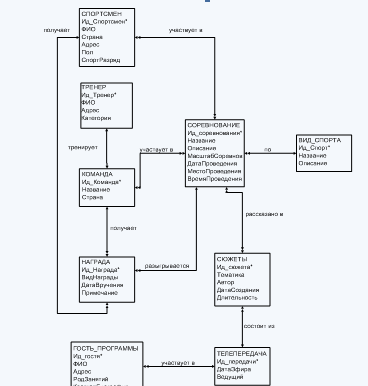
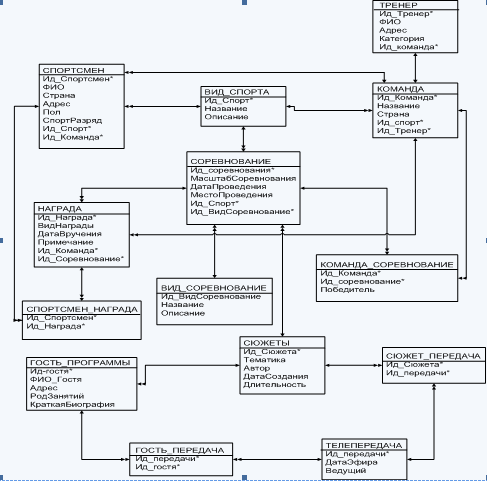
... для предметной области «Спортивная программа» показана на рис.1 Рис.1 – КМД для предметной области «Спортивная программа» Двойная стрелка означает «многие», одинарная стрелка означает «один» во взаимосвязи между объектами. Ключевые атрибуты обозначены *. Описание реляционной модели данных Реляционная модель данных (РМД) представляет БД в виде множества взаимосвязанных отношений, в том ...
... и прикладных программ (логическая независимость данных) и возможность изменения физического расположения и организации данных без изменения общей логической структуры данных и структур данных прикладных программистов (физическая независимость). Рис. 1 2. Системы управления базами данных Использование систем управления базами данных (СУБД) позволяет исключить из прикладных программ ...
... (в виде связей). В последнее время все большее значение приобретает объектно-ориентированный подход к представлению данных. Физическая организация баз данных Физическая организация данных определяет собой способ непосредственного размещения данных на машинном носителе. В современных прикладных программных средствах этот уровень организации обеспечивается автоматически без вмешательства ...
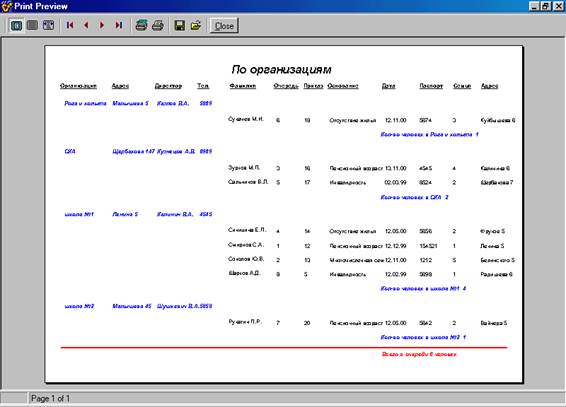
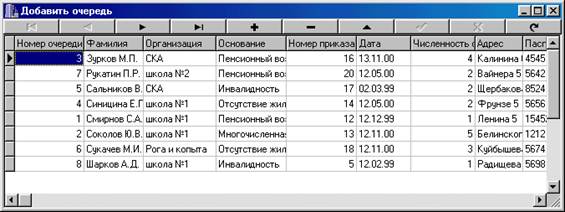
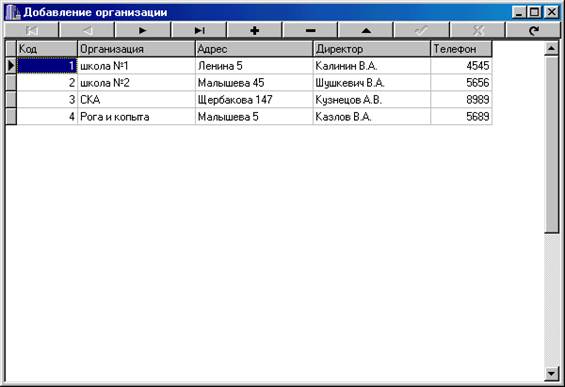
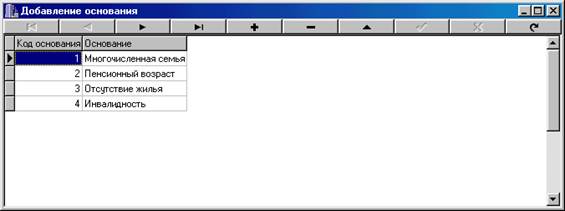
... отчет. Базовый отчет: Отчет по организациям: Программа предназначена для учёта очереди по организациям, а также для предоставления оперативной информации о очереди. К входящей информации относятся: номер очереди, фамилия, организация, основание, номер приказа, дата, численность семьи, адрес , паспорт. Т. е файл: Также Справочник 1 и 2: К выходящей информации в отчёте ...
0 комментариев