Навигация
Правая часть (зависимая часть) каждой ФЗ множества S содержит только один атрибут (т.е. является одноэлементным множеством)
1. Правая часть (зависимая часть) каждой ФЗ множества S содержит только один атрибут (т.е. является одноэлементным множеством).
2. Левая часть (детерминант) каждой ФЗ множества S является неприводимой, т.е. ни один атрибут не может быть опущен из детерминанта без изменения замыкания S+ (без конвертирования множества S в некоторое множество, не эквивалентное множеству S). В таком случае ФЗ является неприводимой слева
3. Ни одна функциональная зависимость в S не может быть опущена из S без изменения замыкания S+ (т.е. без конвертирования множества S в некоторое множество, не эквивалентное множеству S).
Множество зависимостей t, которое неприводимо и эквивалентно некоторому другому множеству зависимостей S, называется неприводимым покрытием множества S. Таким образом, с тем же успехом в системе вместо исходного множества зависимостей S может быть использовано его неприводимое покрытие t. Однако следует отметить, что для заданного множества ФЗ не всегда существует уникальное неприводимое покрытие.
5.6 Нормальные формы – основные понятияПроцесс дальнейшей нормализации, который далее будет упоминаться просто как нормализация, основывается на концепции нормальных форм. Говорят, что отношение находится в некоторой нормальной форме, если удовлетворяет заданному набору условий. Например, отношение находится в первой нормальной форме, или сокращенно в 1 НФ, тогда и только тогда, когда оно содержит только скалярные значения.
Отсюда следует, что каждое нормализованное отношение находится в первой нормальной форме. Иначе говоря, термины "нормализованное" и "1НФ" означают одно и то же. Однако следует отметить, что термин "нормализованное" часто используется для обозначения нормальной формы более высокого уровня, хотя такое обозначение не очень корректно.
 рис. 5.2 Нормальные формы отношений.
рис. 5.2 Нормальные формы отношений.
На рис. 5.2 показано несколько нормальных форм, которые определены к настоящему времени.
Все нормализованные отношения находятся в 1НФ. Некоторые отношения 1НФ находятся также в 2НФ и некоторые отношения 2НФ находятся также в ЗНФ. Мотивом для введения дополнительных определений было то, что вторая нормальная форма "более желательна", чем первая, а третья, в свою очередь, "более желательна", чем вторая. Таким образом, при проектировании базы данных вообще следует использовать отношения не только в первой или во второй, но также и в третьей форме.
Процедуру нормализации можно охарактеризовать как последовательное приведение данного набора отношений к некоторой более желательной форме. Эта процедура обратима, т.е. всегда можно использовать ее результат (например, множество отношений, находящихся в ЗНФ) для обратного преобразования (в исходное отношение, находящееся в 2НФ). Возможность выполнения обратного преобразования является весьма важной характеристикой, поскольку означает, что в процессе нормализации информация не утрачивается
5.7 Декомпозиция без потерь и функциональные зависимостиКак упоминалось ранее, процедура нормализации включает разбиение, или декомпозицию данного отношения на другие отношения, причем декомпозиция должна быть обратимой, т.е. выполняться без потерь информации. Иначе говоря, интерес представляет только те операции, которые выполняются без потерь информации. Вопрос о том, происходит ли утрата информации при декомпозиции, тесно связан с концепцией функциональной зависимости.
Рассмотрим отношение Students из учебной базы данных, с атрибутами {StNo, GrNo, StName, CityNo} (рис. 5.3).
| Students | |||
| StNo | GrNo | StName | CityNo |
| 1 | 1 | Иванов | 1 |
| 2 | 1 | Петров | 3 |
рис. 5.3 Отношение Students.
Ниже приведены две возможные декомпозиции этого отношения (рис. 5.4).
| 1. SGN | SC | ||||
| StNo | GrNo | StName | StNo | CityNo | |
| 1 | 1 | Иванов | 1 | 1 | |
| 2 | 1 | Петров | 2 | 3 | |
| 2. SGN | GC | ||||
| StNo | GrNo | StName | GrNo | CityNo | |
| 1 | 1 | Иванов | 1 | 1 | |
| 2 | 1 | Петров | 1 | 3 | |
рис. 5.4 Возможные декомпозиции отношения Students.
В первом случае информация не утрачивается, поскольку отношения SGN и SC все еще содержат информацию о том, что Иванов живет в городе с кодом 1, Петров – 2. Соединение этих отношений позволяет восстановить исходное отношение Students, иначе говоря первая декомпозиция является декомпозицией без потерь.
Во втором случае информация о городе, в котором проживает студент утрачивается, поскольку студенты, учащиеся в группе с кодом 1 живут в разных городах и зная код группы невозможно однозначно определить код города в котором проживает студент.
Следует отметить, что процесс, который до сих пор назывался “декомпозицией”, на самом деле называется проецированием, т.е. каждое из показанных выше отношений SGN, SC и GC – в действительности являются проекциями исходного отношения Students. Таким образом оператор декомпозиции в процедуре нормализации фактически является оператором проецирования.
Исходное отношение при этом равно соединению его проекций. Для выполнения декомпозиции отношения без потерь необходимо знать, какие условия должны быть соблюдены для того, чтобы при обратном соединении гарантировать получение исходного отношения. Ответ на этот вопрос содержится в теореме Хеза.
Теорема Хеза. Пусть R{A, B, C} является отношением, где A, B, C – атрибуты этого отношения. Если R удовлетворяет зависимости A®B, то отношение R равно соединению его проекций {A, B} и {A, C}.
5.8 Диаграммы функциональных зависимостейНекоторое неприводимое множество зависимостей отношения R можно представить в виде диаграммы функциональных зависимостей (диаграммы ФЗ).
На рис. 5.5 и рис. 5.6 показаны диаграммы ФЗ для некоторых отношений из учебной БД.
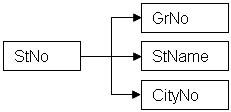 рис. 5.5 Диаграмма ФЗ для таблицы Students.
рис. 5.5 Диаграмма ФЗ для таблицы Students.
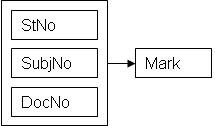 рис. 5.6 Диаграмма ФЗ для таблицы Marks.
рис. 5.6 Диаграмма ФЗ для таблицы Marks.
Как видно из рис. 5.5 и рис. 5.6 каждая стрелка начинается с потенциального ключа (на самом деле с первичного ключа) соответствующего отношения. По определению стрелки должны начинаться с каждого потенциального ключа, поскольку одному значению такого ключа всегда соответствует, по крайней мере, еще одно какое-то значение. Некоторые стрелки следовало бы исключить ввиду того, что очи вызывают определенные трудности, но стрелки, начинающиеся с потенциальных ключей, никогда не могут быть исключены.
Литература:
1. Дейт К.Дж. Введение в системы баз данных. –Пер. с англ. –6-е изд. –К. Диалектика, 1998. Стр. 259–276.
ЛЕКЦИЯ 6. Проектирование БД. Нормальные формы отношений6.1 Первая нормальная форма. Возможные недостатки отношения в 1НФ
6.2 Вторая нормальная форма. Возможные недостатки отношения во 2НФ
6.3 Третья нормальная форма. Возможные недостатки отношения в 3НФ
6.4 Нормальная форма Бойса-Кодда
6.1 Первая нормальная форма. Возможные недостатки отношения в 1НФ
Для простоты изложения предполагается, что каждое отношение имеет в точности один потенциальный ключ, который является первичным ключом. Это допущение подтверждают предлагаемые здесь доказательства. Далее в этой главе будет рассмотрен случай, когда отношение имеет два или более потенциальных ключа.
Отношение находится в первой нормальной форме тогда и только тогда, когда все используемые домены содержат только скалярные значения.
В этом определении всего лишь утверждается, что любое нормализованное отношение находится в 1НФ. Однако отношение, которое находится только в 1 НФ (т.е. не находится ни во второй, ни в третьей нормальной форме) обладает структурой, по некоторым причинам не совсем желательной. Для иллюстрации этого факта допустим, что информация о студентах и оценках содержится не в 2-х отношениях Students и Marks а в одном, назовем его SM.
SM{StNo, CityNo, GrNo, SubjNo, DocNo, Mark}
PRIMARY KEY (StNo, GrNo, SubjNo, DocNo).
Диаграмма функциональных зависимостей этого отношения будет выглядеть как показано на рис. 6.1.
 рис. 6.1 Диаграмма функциональных зависимостей отношения SM
рис. 6.1 Диаграмма функциональных зависимостей отношения SM
Обратите внимание, что диаграммы ФЗ отношения SM “сложнее”, чем диаграммы ФЗ отношений Students и Marks, из которых оно образовано. В диаграммах ФЗ отношений Students и Marks все стрелки начинаются только от первичных ключей, тогда как в диаграмме ФЗ отношения SM появляются дополнительные стрелки. Ниже приведена таблица данных для отношения SM (рис. 6.2).
| SM | ||||||
| StNo | StName | GrNo | CityNo | SubjNo | DocNo | Mark |
| 1 | Иванов | 1 | 1 | 1 | 127 | 5 |
| 1 | Иванов | 1 | 1 | 5 | 128 | 4 |
| 2 | Петров | 1 | 3 | 1 | 127 | 3 |
рис. 6.2 Данные отношения SM.
Несмотря на то, что отношение SM, как и Students и Marks находится в 1й НФ, оно очевидно обладает избыточностью, поскольку, например, в каждом кортеже для студента Иванова указан его номер “1”, код его группы – “1” и код города, в котором он проживает – “1”. Аналогичная ситуация с другими студентами.
Избыточность в отношении SM приводит к разным аномалиям обновления, получившим такое название по историческим причинам, т.е. к трудностям при выполнении операций обновления типа INSERT (вставка), DELETE (удаление) и UPDATE (обновление). Для начала рассмотрим избыточность типа студент—код города студента, соответствующую функциональной зависимости StNo ®CityNo, и перечисленные ниже проблемы с операциями обновления.
Операция вставки (INSERT). Нельзя вставить данные о студенте, проживающем в некотором городе, не указывая хотя бы одну, полученную этим студентом, оценку. Действительно, в таблице SM не показан студент Сидоров из г. Пятихатки потому, что до тех пор, пока этот студент не получит оценку по какому либо предмету, для него не задано значение первичного ключа.
Операция удаления (DELETE). Если удалить единственный кортеж отношения SM для некоторого студента, будет удалена не только информация о соответствующей оценке, но и информация о студенте и городе, в котором он проживает. Например, если в отношении SM удалить кортеж со значением Петров атрибута StName, будет утрачена вся информация об этом студенте.
Замечание. В действительности проблема заключается в том, что в отношении SM содержится очень много совместной информации, поэтому при удалении некоторого кортежа приходится удалять слишком иного другой информации. А точнее, отношение SM содержит информацию о студентах и об оценках. Таким образом, удаление информации об оценке вызывает также удаление информации о студенте. Для решения этой проблемы нужно разделить информацию на несколько частей, т.е. разместить информацию о студентах в одном отношении, а об оценках – в другом. Таким образом, неформально процедуру нормализации можно охарактеризовать как процедуру разбиения логически несвязанной информации по отдельным отношениям.
Операция модификации (UPDATE). Фамилия студента и код города, в котором он проживает повторяется в отношении SM множество раз, и это приводит к возникновению проблем при обновлении. Если студент меняет фамилию или переезжает в другой город, то возникает проблема, связанная либо с поиском в отношении SM всех кортежей, в которых присутствует информация об этом студенте, либо с получением несовместимого результата (в одном кортеже городом проживания студента будет один город, а в другом кортеже, городом проживания этого студента, будет другой город).
Для решения проблемы избыточности, которая характерна для отношения SM достаточно заменить его двумя другими:
Students{StNo, GrNo, StName, CityNo}
и
Marks{StNo, SubjNo, DocNo, Mark}
Важно отметить, что переработанная таким образом структура позволяет преодолеть все перечисленные ранее проблемы, связанные с операциями обновления.
Операция вставки (INSERT). Теперь с помощью вставки соответствующего кортежа в отношение Students можно включить информацию о студенте и городе, в котором он проживает, даже если он в настоящий момент не получил не одной оценки.
Операция удаления (DELETE). Теперь можно исключить информацию об оценке, удаляя соответствующий кортеж из отношения Marks, при этом информация о студенте и городе, в котором он проживает, не утрачивается.
Операция модификации (UPDATE). В переработанной структуре фамилия студента и информация о городе, в котором он проживает, появляется всего один раз, поскольку существует только один кортеж для данного студента в отношении Students (атрибут StNo является первичным ключом для такого отношения). Иначе говоря, избыточность данных StNo-StName-StCity устранена. Благодаря этому теперь можно один раз изменить в соответствующем кортеже отношения Students название города для какого-либо студента.
6.2 Вторая нормальная форма. Возможные недостатки отношения во 2НФ
Определим 2НФ при условии, что существует только один потенциальный ключ, который является первичным ключом.
Отношение находится во второй нормальной форме тогда и только тогда, когда оно находится в первой нормальной форме и каждый неключевой атрибут неприводимо зависим от первичного ключа.
Оба отношения, Students и Marks находятся во второй нормальной форме с первичными ключами StNp и {StNo, SubjNo, DocNo} соответственно, а отношение SM не находится в ней. Всякое отношение, которое находится в 1НФ и не находится в 2НФ, всегда можно свести к эквивалентному набору отношений, находящихся в 2НФ.
Рассмотрим другой пример. Предположим, информация о коде города, названии города и области, в которой этот город расположен находятся в одной таблице CNR{CityNo, CityName, RgNo, RgName} (рис. 6.3).
| CNR | |||
| CityNo | CityName | RgNo | RgName |
| 1 | Желтые Воды | 1 | Днепропетровская |
| 2 | Кривой Рог | 1 | Днепропетровская |
| 3 | Пятихатки | 1 | Днепропетровская |
| 4 | Львов | 2 | Львовская |
рис. 6.3 Данные отношения CNR.
Диаграмма ФЗ отношения CNR выглядит следующим образом – рис. 6.4.
 рис. 6.4 Функциональные зависимости в отношении CNR.
рис. 6.4 Функциональные зависимости в отношении CNR.
Как видно из рис. 6.3, это диаграмма ФЗ “сложнее” диаграмм ФЗ отношений Cities и Regions. Несмотря на то, что отношение CNR находится во 2НФ, оно обладает некоторой избыточностью, связанной с наличием транзитивной ФЗ между атрибутами CityNo и RgName. Транзитивная зависимость приводит к следующим аномалиям обновления.
Операция вставки (INSERT). Нельзя включить данные о некоторой области, например, нельзя указать, что существует Львовская область, до тех пор пока не появиться запись о городе, находящемся в данной области, – например о Львове.
Операция удаления (DELETE). При удалении из отношения CNR последнего кортежа для некоторого города будет удалена не только информация о данном городе, но также информация о том, в какой области этот город находился. Например, при удалении из отношения CNR кортежа для города Львов будет утрачена информация о Львовской области.
Замечание. Вновь причиной этих неприятностей является совместная информация: отношение CNR содержит информацию о городах вместе с информацией об областях. Для разрешения этой ситуации следует поступить так, как и раньше, т.е. ''разобрать" всю эту информацию и перенести в одно отношение сведения об областях, а в другое – сведения о городах.
Операция модификации (UPDATE). В отношении CNR код и название области для каждого города повторяется несколько раз (поэтому оно характеризуется некоторой избыточностью). Таким образом, при изменении кода области возникнет либо проблема необходимости поиска в отношении CNR всех кортежей для этой области (для внесения соответствующих изменений), либо проблема получения несовместимого результата.
Для решения этих проблем необходимо заменить отношение CNR двумя проекциями:
Cities{CityNo, CityName, RgNo}
Regions{RgNo, RgName}
Переработанная таким образом структура отношений позволит преодолеть все описанные проблемы с операциями обновления.
6.3 Третья нормальная форма. Возможные недостатки отношения в 3НФОтношение находится в третьей нормальной форме тогда и только тогда, когда оно находится во второй нормальной форме и каждый неключевой атрибут нетранзитивно зависит от первичного ключа. (Под "нетранзитивной зависимостью" подразумевается отсутствие какой-либо взаимной зависимости в изложенном выше смысле.)
Отношения Cities и Regions находятся в третьей нормальной форме. Таким образом вторым этапом нормализации является создание проекций для исключения транзитивных зависимостей.
6.3.1 Сохранение зависимостиВ процессе приведения отношений часто возникают ситуации, когда данное отношение может быть подвергнуто операции декомпозиции разными способами. Рассмотрим снова приведенное выше отношение CNR с функциональными зависимостями CityNo®CityName, CityNo®RgNo, CityNo®RgNаме, RgNo®RgName и, следовательно, транзитивной зависимостью CityNo®RgName (на рис. 6.5 транзитивная зависимость показана пунктирной стрелкой).
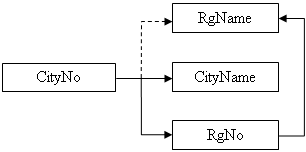 рис. 6.5 Функциональные зависимости в отношении CNR
рис. 6.5 Функциональные зависимости в отношении CNR
Выше отмечалось, что аномалии обновления, которые сопровождают отношение CNR, можно преодолеть с помощью декомпозиции с заменой этого отношения двумя проекциями в ЗНФ.
Cities{CityNo, CityName, RgNo} и Regions{RgNo, RgName}
Назовем эту декомпозицию просто "декомпозицией №1", имея в виду, что для нее существует альтернативная "декомпозиция №2":
Cities{CityNo, CityName, RgNo} и Regions{CityNo, RgName}
При этом обе проекции Cities одинаковы как для №1, так и для №2. Декомпозиция №2 происходит также без потери информации, а обе ее проекции находятся в ЗНФ. Однако по некоторым причинам декомпозиция №2 менее желательна, чем декомпозиция №1. Например, после выполнения декомпозиции №2 все еще невозможно вставить информацию о том, что некоторая область имеет определенный код, без указания города, который находится в этой области.
Рассмотрим этот пример подробнее. Прежде всего заметим, что зависимости проекций в декомпозиции №1 отмечены сплошными стрелками, тогда как одна, из зависимостей проекций декомпозиции №1 отмечена пунктирной стрелкой. В декомпозиции №1 две проекции независимы друг от друга в следующем смысле: обновления в каждой из проекций могут быть выполнены совершенно независимо друг от друга. (Конечно, за исключением ограничения целостности для Cities и Regions) Если такое обновление допустимо только в контексте данной проекции, т.е. не нарушается уникальность первичного ключа для этой проекции, то соединение этих двух проекций после обновления всегда будет равносильно отношению CNR (т.е. при соединении не будут нарушены ограничения, наложенные на ФЗ в отношении CNR). В декомпозиции №2, наоборот, обновление любой из двух проекций должно тщательно фиксироваться, чтобы гарантировать отсутствие нарушения зависимости RgNo®RgName (если два города находятся в одной и той же области, они должны иметь одинаковый код области). Иначе говоря, обе проекции декомпозиции №2 не являются независимыми одна от другой.
Основная проблема заключается в том, что в декомпозиции №2 функциональная зависимость RgNo®RgName становится ограничением между отношениями. (Следует отметить, что во многих современных программных продуктах это ограничение должно поддерживаться с помощью процедурной обработки.) В декомпозиции №1, наоборот, транзитивная зависимость SityNo®RgName является ограничением между отношениями, которое автоматически выполняется при задействовании двух ограничений внутри отношений: CityNo®RgNo и RgNo®RgName. Привести в действие эти ограничения достаточно просто за счет соответствующих ограничений, наложенных на уникальность первичных ключей.
Концепция независимых проекций, таким образом, обеспечивает критерий выбора одной из нескольких возможных декомпозиции. Декомпозиция с независимыми проекциями в приведенном выше общем смысле предпочтительнее той, в которой проекции зависимы. Риссанен (Rissanen) показал, что проекции R1 и R2 отношения R независимы в упомянутом выше смысле тогда и только тогда, когда:
1. каждая ФЗ в отношении R является логическим следствием функциональных зависимостей в проекциях R1 и R2;
2. общие атрибуты проекций R1 и R2 образуют потенциальный ключ, по крайней мере, для одной из них.
Отношение, которое не может быть подвергнуто декомпозиции с получением независимых проекций, называется атомарным. Однако это не значит, что любое неатомарное отношение может быть разбито на атомарные компоненты. Идея нормализации с декомпозицией на независимые проекции называется декомпозицией с сохранением зависимости.
6.4 Нормальная форма Бойса-КоддаВ этом разделе опускается упрощающее допущение о том, что каждое отношение имеет только один потенциальный ключ (а именно первичный ключ), и рассматривается более общий случай. Оригинальное определение Кодда для ЗНФ не совсем подходит для отношений с перечисленными ниже условиями.
1. Отношение имеет два (или более) потенциальных ключа.
2. Два потенциальных ключа являются сложными.
3. Они перекрываются (т.е. имеют, по крайней мере, один общий атрибут).
Поэтому оригинальное определение ЗНФ было впоследствии заменено более строгим определением Бойса-Кодда (Boyce/Codd), для которого было принято отдельное название – нормальная форма Бойса-Кодда, НФБК. (На самом деле строгое определение "третьей" нормальной формы, эквивалентное определению нормальной формы Бойса-Кодда, было впервые дано Хезом (Heath) в 1971 году, и этой форме следовало бы дать название "нормальная форма Хеза".)
Замечание. Комбинация условий 1, 2 и 3 не часто встречается на практике, и для отношения без этих условий ЗНФ и НФБК эквивалентны.
Отношение находится в нормальной форме Бойса-Кодда тогда и только тогда, когда каждая нетривиальная и неприводимая слева ФЗ обладает потенциальным ключом в качестве детерминанта.
Менее формальное определение имеет другую формулировку: отношение находится в нормальной форме Бойса-Кодда тогда и только тогда, когда детерминанты являются потенциальными ключами.
Иначе говоря, на диаграмме ФЗ стрелки будут начинаться только с потенциальных ключей. Согласно данному определению никакие другие стрелки не допускаются.
Примером отношения, которое находится в НФБК может служить отношение Students, в которое добавлен атрибут IdCode – идентификационный код.
Students {StNo, IdCode, GrNo, StName, CityNo}
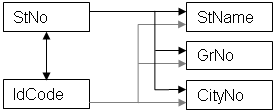 рис. 6.6 Диаграмма ФЗ расширенного отношения, Students, находящегося в НФБК.
рис. 6.6 Диаграмма ФЗ расширенного отношения, Students, находящегося в НФБК.
В этом отношении детерминанты являются потенциальными ключами, а все стрелки начинаются с потенциальных ключей. Рассмотрим отношение, не находящееся в НФБК.
Предположим, что информация об идентификационных кодах студентов хранится в отношении Marks. Назовем модифицированное отношение MI {StNo, IdCode, SubjNo, DocNo, Mark} (рис. 6.7).
| MI | ||||
| StNo | IdCode | SubjNo | DocNo | Mark |
| 1 | 2895764537 | 1 | 127 | 5 |
| 1 | 2895764537 | 5 | 128 | 4 |
| 2 | 3094769520 | 1 | 127 | 3 |
| 2 | 3094769520 | 5 | 128 | 3 |
| 3 | 2984267527 | 1 | 127 | 5 |
рис. 6.7 Данные отношения MI.
В этом отношении присутствуют 2 потенциальных ключа {StNo, SubjNo, DocNo} и {IdCode, SubjNo, DocNo}. Отношение находится в 3-й НФ, но не находится в НФБК, так как содержит два детерминанта, которые не являются потенциальными ключами этого отношения (StNo и IdCode детерминанты, поскольку они определяют друг друга). Как видно, в отношении MI присутствует доля избыточности, которая имелась и в ранее рассмотренных отношениях (SM и CNR), поэтому оно характеризуется такими же аномалиями обновления. Для решения этой проблемы отношение MI следует разбить на две проекции:
SI {StNo, IdCode} и Marks {StNo, SubjNo, DocNo, Mark}
или другим способом
SI {StNo, IdCode} и Marks {IdCode, SubjNo, DocNo, Mark}
Т.о. присутствуют две, в одинаковой мере допустимые декомпозиции, причем все проекции отношения MI находятся в НФБК. Исходя из соображений здравого смысла первая декомпозиция лучше, поскольку в учебной БД для идентификации студента используется его код StNo.
Литература:
1. Дейт К.Дж. Введение в системы баз данных. –Пер. с англ. –6-е изд. –К. Диалектика, 1998. Стр. 279–301.
ЛЕКЦИЯ 7. Проектирование БД. Нормальные формы отношений (продолжение)7.1 Многозначные зависимости
7.2 Четвертая нормальная форма
7.3 Зависимости соединения
7.4 Пятая нормальная форма
7.5 Итоговая схема процедуры нормализации
7.1 Многозначные зависимости
Пусть дано ненормализованное отношение UCTX (т.е. отношение, которое не находится в 1НФ), содержащее информацию о курсах обучения, преподавателях и учебниках. Каждый кортеж такого отношения состоит из названия курса (Course), a также групп имен преподавателей (Teachers) и названий учебников (Texts) – на рис. 7.1 показаны два таких кортежа. Под этим подразумевается, что каждый курс может преподаваться любым преподавателем соответствующей группы с использованием всех указанных учебников. Предположим, что для заданного курса может существовать любое количество соответствующих преподавателей и соответствующих учебников. Более того, допустим, хотя это и не совсем реалистичное допущение, что преподаватели и рекомендуемые учебники совершенно независимы друг от друга. Это значит, что независимо от того, кто преподает данный курс, всегда используется один и тот же набор учебников. Наконец, допустим, что определенный преподаватель или определенный учебник могут быть связан с любым количеством курсов.
| UCTX | ||
| COURSE | TEACHERS | TEXTS |
| Физика | проф. Иванов проф. Петров | основы механики оптика |
| Математика | проф. Иванов | основы механики дискретная математика тригонометрия |
рис. 7.1 Ненормализованное отношения UCTX
Преобразуем это отношение в эквивалентное нормализованное отношение. Следует заметить, что для рассматриваемых данных функциональные зависимости не заданы (за исключением тривиальных зависимостей типа Course ® Course). Поэтому высказанные в предыдущей главе идеи не позволяют создать никакой формальной основы для выполнения декомпозиции данного отношения на проекции.
| CTX | ||
| COURSE | TEACHER | TEXT |
| Физика | проф. Иванов | основы механики |
| Физика | проф. Иванов | оптика |
| Физика | проф. Петров | основы механики |
| Физика | проф. Петров | оптика |
| Математика | проф. Иванов | основы механики |
| Математика | проф. Иванов | дискретная математика |
| Математика | проф. Иванов | тригонометрия |
рис. 7.2 Таблица нормализованного отношения CTX.
В простейшей формулировке нормализованное отношение CTX означает, что кортеж {Course:c, Teacher:t, Техт:x} появляется в данном отношении тогда и только тогда, когда курс c читается преподавателем t с использованием учебника x. Тогда, принимая во внимание допустимость существования для данного отношения всех возможных комбинаций преподавателей вместе с учебниками, можно утверждать, что для отношения CTX верно следующее ограничение: если присутствуют оба кортежа (c,tl,xl) и (c,t2,x2), тогда присутствуют также оба кортежа (c,tl,x2) и (c,t2,xl)
Очевидно, что отношение CTX характеризуется значительной избыточностью и приводит к возникновению аномалий обновления. Например, для добавления информации о том, что курс физики может читаться новым преподавателем, необходимо создать два новых кортежа, по одному для каждого учебника. Тем не менее, отношение CTX находится в НФБК, поскольку является "полностью ключевым".
Можно заметить, что ситуация может быть исправлена к лучшему, если заменить отношение СТХ его проекциями {Course, Teacher} и {Course, Text}, показанными на рис. 7.3. Обе проекции являются "полностью ключевыми" и находятся в НФБК; более того, отношение СТХ может быть восстановлено с помощью обратного соединения проекций СТ и СХ и потому данная композиция выполняется без потерь. Однако только в 1971 году эти интуитивные идеи были сформулированы Фейгином (Fagin) в строгом теоретическом виде с помощью понятия многозначных зависимостей.
| CT | СХ | |||
| COURSE | TEACHER | COURSE | TEXT | |
| физика | проф. Иванов | физика | основы механики | |
| физика | проф. Петров | физика | оптика | |
| математика | проф. Иванов | математика | основы механики | |
| математика | дискретная математика | |||
| математика | тригонометрия | |||
рис. 7.3 Таблицы проекций СТ и СХ
Возвращаясь к рассматриваемому примеру с действительно корректной и желательной декомпозицией, показанной на рис. 7.3, следует, однако, отметить, что такая декомпозиция не может быть выполнена на основе функциональных зависимостей, поскольку они не существуют в данном отношении (кроме тривиальных зависимостей). Однако ее можно осуществить на основе нового типа зависимости, а именно упомянутой выше многозначной зависимости. Многозначные зависимости можно считать обобщением функциональных зависимостей в том смысле, что каждая функциональная зависимость является многозначной (однако обратное утверждение не верно, поскольку существуют многозначные зависимости, которые не являются функциональными). В отношении СТХ есть две многозначные зависимости:
Course—>>Teacher
Course—>>Text
Обратите внимание на двойную стрелку, которая в многозначной зависимости A—>>B означает, что "B многозначно зависит от A" или "A многозначно определяет B".
Пусть A, B и C являются произвольными подмножествами множества атрибутов отношения R. Тогда B многозначно зависит от A, что символически выражается записью
А—>>В
тогда и только тогда, когда множество значений B, соответствующее заданной паре (значение A, значение C) отношения R, зависит только от A, но не зависит от C.
Для данного отношения R{A, B, C} многозначная зависимость A—>>B выполняется тогда и только тогда, когда также выполняется многозначная зависимость A —>> C. Таким образом, многозначные зависимости всегда образуют связанные пары и потому их обычно представляют вместе в символическом виде:
А—>>В|С.
Для рассматриваемого примера такая запись будет иметь следующий вид:
Course—>>Teacher|Text
Возвращаясь к исходной задаче с отношением СТХ, теперь можно отметить, что описанная ранее проблема с отношением типа СТХ возникает из-за того, что оно содержит многозначные зависимости, которые не являются функциональными. (Следует отметить совсем неочевидный факт, что именно наличие таких МЗ требует вставлять два кортежа, когда необходимо добавить данные еще об одном преподавателе физики.) Проекции СТ и СХ не содержат многозначных зависимостей, а потому они действительно представляют собой некоторое усовершенствование исходной структуры. Поэтому было бы желательно заменить отношение СТХ двумя этими проекциями. Это можно сделать, исходя из теоремы Фейгина, которая приведена ниже.
Теорема Фейгина (эта теорема является более строгой версией теоремы Хеза). Пусть А, В и С являются множествами атрибутов отношения R{A, В, С}. Отношение R будет равно соединению его проекций {А, В} и {А, С} тогда и только тогда, когда для отношения R выполняется многозначная зависимость А—>>В|С.
7.2 Четвертая нормальная формаОтношение R находится в четвертой нормальной форме (4НФ) тогда и только тогда, когда существуют такие подмножества А и В атрибутов отношения R, что выполняется (нетривиальная) многозначная зависимость А —>> В. Тогда все атрибуты отношения R также функционально зависят от атрибута A.
7.3 Зависимости соединенияДо сих пор предполагалось, что единственной операцией в процессе декомпозиции является замена данного отношения (при декомпозиции без потерь) двумя его проекциями. Это допущение успешно выполнялось вплоть до определения 4НФ. Однако существуют отношения, для которых нельзя выполнить декомпозицию без потерь на две проекции, но которые можно подвергнуть декомпозиции без потерь на три или более проекции.
На рисунке представлен пример конкретного набора данных, соответствующих некоторому моменту времени. Однако, если данное отношение удовлетворяет некоторому не зависящему от времени ограничению, то 3-декомпозируемость отношения TSG может быть более фундаментальным и не зависящим от времени свойством, т.е. свойством, которое удовлетворяется для всех допустимых значений данного отношения. Для того чтобы понять, каким должно быть такое отношение, прежде всего отметим, что утверждение "отношение TSG равно соединению трех проекций TS, SG и TG" эквивалентно следующему утверждению:
Если пара (t1,s1) находится в отношении TS и пара (s1,g1) находится в отношении SG и пара (t1,g1) находится в отношении TG то тройка (t1,s1,g1) находится в отношении TSG.
| TSG | ||
| TEACHER | SUBJECT | GROUP |
| Иванов | Математика | А-98-51 |
| Иванов | Физика | Б-00-51 |
| Петров | Математика | А-99-51 |
| Петров | Физика | А-98-51 |
| TS | SG | TG | ||||||||||||
| TEACHER | SUBJECT | SUBJECT | GROUP | TEACHER | GROUP | |||||||||
| Иванов | Физика | Математика | А-99-51 | Иванов | А-98-51 | |||||||||
| Иванов | Математика | Математика | А-98-51 | Иванов | Б-00-51 | |||||||||
| Петров | Физика | Физика | А-98-51 | Петров | А-99-51 | |||||||||
| Петров | Математика | Физика | Б-00-51 | Петров | А-98-51 | |||||||||
| ëСоединение по Subjectû ¯ | ||||||||||||||
| TEACHER | SUBJECT | GROUP | ||||||||||||
| Иванов | Физика | А-98-51 | ||||||||||||
| Иванов | Физика | Б-00-51 | ||||||||||||
| Иванов | Математика | А-99-51 | ||||||||||||
| Иванов | Математика | А-98-51 | ||||||||||||
| Петров | Физика | А-98-51 | ||||||||||||
| Петров | Физика | Б-00-51 | ||||||||||||
| Петров | Математика | А-99-51 | ||||||||||||
| Петров | Математика | А-98-51 | ||||||||||||
| ëСоединение по комбинации Teacher и Groupû ¯ | ||||||||||||||
| Исходное TSG | ||||||||||||||
рис. 7.4 Отношение TSG является соединением трех бинарных проекций.
Исходя из этих заключений можно сказать, что пара (t1,s1) присутствует в отношении TS тогда и только тогда, когда тройка (t1, s1, g2) присутствует в отношении TSG для некоторого значения g2. Тогда приведенное выше утверждение можно переписать в виде ограничения, накладываемого на отношение SPJ:
Если (t1,s1,g2), (t2,s1,g1), (t1,s2,g1) находятся в отношении TSG то (t1,s1,g1) также находится в отношении TSG.
Если это утверждение выполняется всегда, т.е. для всех допустимых значений отношения TSG, то тем самым будет получено независящее от времени (хотя и несколько странное) ограничение для данного отношения. Обратите внимание на циклическую структуру этого ограничения. Отношение будет n-декомпозируемым для n>2 тогда и только тогда, когда оно удовлетворяет некоторому циклическому ограничению.
Циклическое ограничение с практической точки зрения обозначает, что, например, если:
1. Петров преподает математику;
2. математика преподается в А-98-51;
3. Петров преподает в А-98-51
то:
4. Петров преподает математику в А-98-51.
Обратите внимание, что из взятых вместе условий (1), (2) и (3) не следует (4).
Пусть R является отношением, а А, В,..., Z— произвольными подмножествами множества атрибутов отношения R. Отношение R удовлетворяет зависимости соединения
* (A, B, ..., Z)
тогда и только тогда, когда оно равносильно соединению своих проекций с подмножествами атрибутов А, В, ..., Z.
Отсюда ясно, что отношение TSG с зависимостью соединения *(TS, SG, TG) может быть 3-декомпозируемым. Однако следует ли выполнять такую декомпозицию? По всей видимости, да, так как отношение TSG характеризуется многочисленными аномалиями обновления, которые можно устранить с помощью 3-декомпозиции. Пример был приведен при определении циклического ограничения, из-за наличия которого, в отношении TSG должен присутствовать следующий кортеж (рис. 7.5)
| TEACHER | SUBJECT | GROUP |
| Петров | Математика | А-98-51 |
рис. 7.5 Дополнительный кортеж.
Также теорема Фейгина может быть сформулирована следующим образом: отношение R{A, В, С} удовлетворяет зависимости соединения *(АВ, АС) тогда и только тогда, когда оно удовлетворяет многозначной зависимости А —>> В | С.
Эту теорему можно использовать в качестве определения многозначной зависимости, отсюда следует, что многозначная зависимость является частным случаем зависимости соединения. Более того, из определения зависимости соединения следует, что из всех возможных форм это наиболее общая форма зависимости.
Возвращаясь к рассматриваемому примеру, можно обнаружить следующую проблему: отношение TSG содержит зависимость соединения, которая не является ни многозначной, ни функциональной зависимостью. Можно также заметить, что рекомендуется декомпозировать такое отношение на меньшие компоненты, а именно на проекции, заданные зависимостью соединения. Такой процесс декомпозиции может повторяться до тех пор, пока все результирующие отношения не будут находиться в пятой нормальной форме.
7.4 Пятая нормальная формаОтношение R находится в пятой нормальной форме (5НФ), которая также называется проекционно-соединительной нормальной формой, тогда и только тогда, когда каждая зависимость соединения в отношении R подразумевается потенциальными ключами отношения R.
Отношение TSG не находится в 5НФ. Оно удовлетворяет некоторой зависимости соединения, а именно ЗД-ограничению, которое, конечно, не подразумевается его единственным потенциальным ключом. Наоборот, после 3-декомпозиции проекции TS, SG и GT находятся в 5НФ, поскольку для них вовсе нет зависимостей соединения.
7.4.1 Зависимости соединения, подразумеваемой потенциальными ключамиРассмотрим простой пример, в котором дано отношение с данными студентов Students с потенциальным ключом StNo. Такое отношение удовлетворяет нескольким зависимостям соединения, например зависимости
* ( (StNo, GrNo, StName), (StNo, CityNo) ).
Это значит, что отношение Students равносильно соединению его проекций с атрибутами {StNo, GrNo, StName} и {StNo, CityNo}, а потому может быть подвергнуто декомпозиции без потерь на указанные проекции. (Заметьте, что его не следует, а можно подвергнуть декомпозиции.) Существование этой зависимости соединения следует (или подразумевается) из того, что StNo является потенциальным ключом (в действительности это следует из теоремы Хеза).
В заключение заметим, что, как следует из определения 5НФ, она является окончательной нормальной формой по отношению к проекции и соединению. Таким образом, гарантируется, что отношение в пятой нормальной форме не содержит аномалий, которые могут быть исключены разбиением на проекции.
7.5 Итоговая схема процедуры нормализацииПусть дано отношение R, которое находится в 1НФ (или может быть приведено к такой форме после выравнивания исходной ненормализованной структуры), вместе с некоторыми ограничениями (функциональными зависимостями, многозначными зависимостями и зависимостями соединения). Тогда основная идея этой технологии состоит в систематическом приведении отношения R к набору меньших отношений, который в некотором заданном смысле эквивалентен отношению R, но более предпочтителен. Каждый этап процесса приведения состоит из разбиения на проекции отношений, полученных на предыдущем этапе, таким образом, чтобы проекции находились в нормальной форме более высокого порядка, чем первоначальное отношение.
Из приведенных выше правил можно выделить некоторые особенности.
1. Прежде всего, процесс разбиения на проекции на каждом этапе должен быть выполнен без потерь и с сохранением зависимости (там, где это возможно).
2. Необходимо подчеркнуть тот факт, что могут существовать соображения, по которым нормализацию не следует выполнять полностью.
Пятая нормальная форма является окончательной в том смысле, что дальнейшее устранение аномалий невозможно путем разбиения исходного отношения на проекции. Существуют нормальные формы более высоких порядков, однако они крайне редко встречаются на практике и в данном курсе не рассматриваются.
Литература:
1. Дейт К.Дж. Введение в системы баз данных. –Пер. с англ. –6-е изд. –К. Диалектика, 1998. Стр. 309–328.
ЛЕКЦИЯ 8. Проектирование БД методом сущность-связь. ER-диаграммы8.1 Возникновение семантического моделирования
8.2 Основные понятия метода
8.3 Диаграммы ER-экземпляров и ER-типа
8.4 Правила формирования отношений
8.5 Методология IDEF1 (самостоятельное изучение)
8.1 Возникновение семантического моделирования
Широкое распространение реляционных СУБД и их использование в самых разнообразных приложениях показывает, что реляционная модель данных достаточна для моделирования предметных областей. Однако проектирование реляционной базы данных в терминах отношений на основе механизма нормализации часто представляет собой очень сложный и неудобный для проектировщика процесс. Потребности проектировщиков баз данных в более удобных и мощных средствах моделирования предметной области вызвали к жизни направление семантических моделей данных. В этой лекции рассматривается одна из популярных семантических моделей данных – модель "сущность–связь".
Метод сущность-связь называют также методом "ER-диаграмм": во-первых, ER –аббревиатура от слов Essence (сущность) и Relation (связь), во-вторых, метод основан на использовании диаграмм, называемых соответственно диаграммами ER-экземпляров и диаграммами ER-типа.
8.2 Основные понятия методаОсновными понятиями метода сущность-связь являются следующие:
1. сущность – представляет собой объект, информация о котором хранится в БД. Экземпляры сущности отличаются друг от друга и однозначно идентифицируются. Названиями сущностей являются, как правило, существительные, например: ПРЕПОДАВАТЕЛЬ, ДИСЦИПЛИНА, ГРУППА.
2. Атрибут сущности – представляет собой свойство сущности. Это понятие аналогично понятию атрибута в отношении. Так, атрибутами сущности ПРЕПОДАВАТЕЛЬ может быть его Фамилия, Должность, Стаж (преподавательский) и т. д.
3. Ключ сущности – атрибут или набор атрибутов, используемый для идентификации экземпляра сущности. Как видно из определения, понятие ключа сущности аналогично понятию ключа отношения.;
4. Связь между сущностями. Связь двух или более сущностей - предполагает зависимость между атрибутами этих сущностей. Название связи обычно представляется глаголом. Примерами связей между сущностями являются следующие- ПРЕПОДАВАТЕЛЬ ВДЕТ ДИСЦИПЛИНУ (Иванов ВЕДЕТ "Организацию БД и знаний"), ПРЕПОДАВАТЕЛЬ ПРЕПОДАЕТ В ГРУППЕ (Иванов ПРЕПОДАЕТ В 256 группе);
5. Степень связи – является характеристикой связи между сущностями, которая может быть следующих видов: 1:1, 1:М, М:1, М:М.;
6. Класс принадлежности (КП) экземпляров сущности. КП сущности может быть: обязательным и необязательным. Класс принадлежности сущности является обязательным, если все экземпляры этой сущности обязательно участвуют в рассматриваемой связи, в противном случае класс принадлежности сущности является необязательным.
7. Диаграммы ER-экземпляров;
8. Диаграммы ER-типа.
Приведенные определения сущности и связи не полностью формализованы, но приемлемы для практики. Следует иметь в виду, что в результате проектирования могут быть получены несколько вариантов одной и той же БД. Так, два разных проектировщика, рассматривая одну и ту же проблему с разных точек зрения, могут получить различные наборы сущностей и связей. При этом оба варианта могут быть рабочими, а выбор лучшего из них будет результатом личных предпочтений.
8.3 Диаграммы ER-экземпляров и ER-типаС целью повышения наглядности и удобства проектирования для представления сущностей, экземпляров сущностей и связей между ними используются следующие графические средства:
Похожие работы
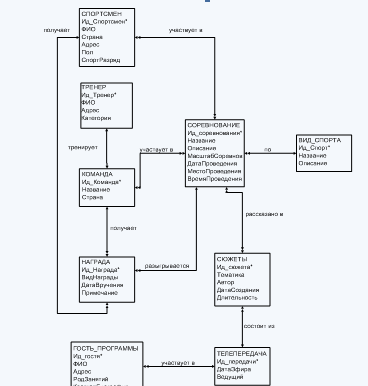
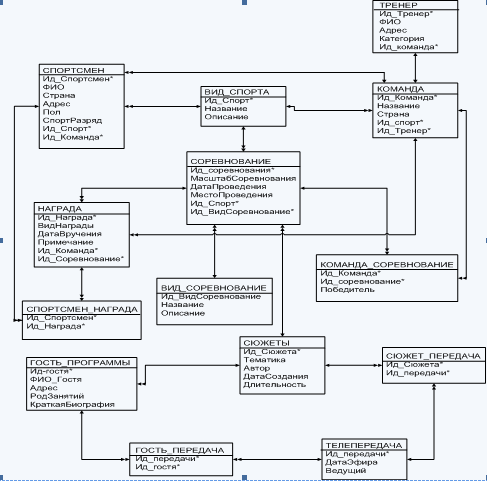
... для предметной области «Спортивная программа» показана на рис.1 Рис.1 – КМД для предметной области «Спортивная программа» Двойная стрелка означает «многие», одинарная стрелка означает «один» во взаимосвязи между объектами. Ключевые атрибуты обозначены *. Описание реляционной модели данных Реляционная модель данных (РМД) представляет БД в виде множества взаимосвязанных отношений, в том ...
... и прикладных программ (логическая независимость данных) и возможность изменения физического расположения и организации данных без изменения общей логической структуры данных и структур данных прикладных программистов (физическая независимость). Рис. 1 2. Системы управления базами данных Использование систем управления базами данных (СУБД) позволяет исключить из прикладных программ ...
... (в виде связей). В последнее время все большее значение приобретает объектно-ориентированный подход к представлению данных. Физическая организация баз данных Физическая организация данных определяет собой способ непосредственного размещения данных на машинном носителе. В современных прикладных программных средствах этот уровень организации обеспечивается автоматически без вмешательства ...
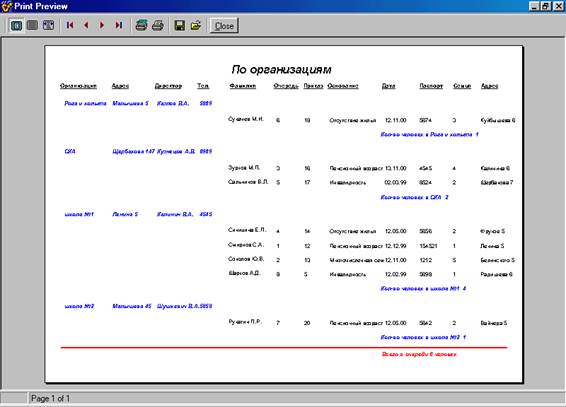
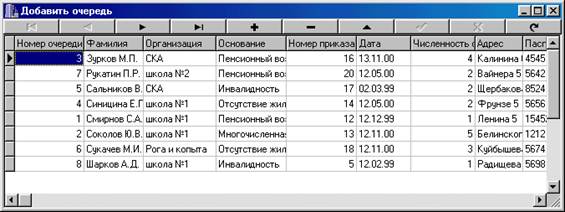
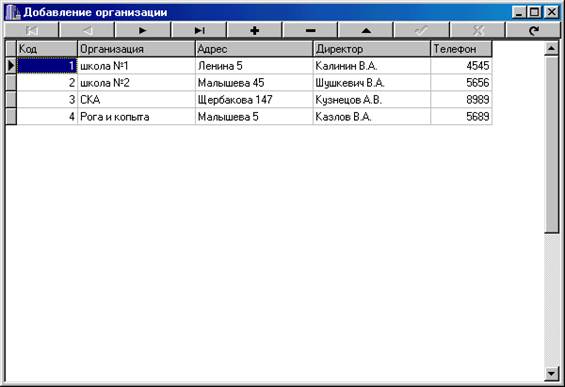
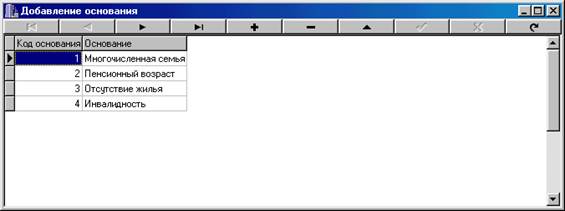
... отчет. Базовый отчет: Отчет по организациям: Программа предназначена для учёта очереди по организациям, а также для предоставления оперативной информации о очереди. К входящей информации относятся: номер очереди, фамилия, организация, основание, номер приказа, дата, численность семьи, адрес , паспорт. Т. е файл: Также Справочник 1 и 2: К выходящей информации в отчёте ...
0 комментариев