Сглаживание ландшафта

2.1.2 Сглаживание ландшафта

Построение ландшафта может быть произведено сразу после триангуляции равномерной сетки, но в этом случае очертания ландшафта будут резкими. Если это нежелательно, то можно воспользоваться методом сглаживания, реализованным в данной работе.

Его суть заключается в следующем. В процессе сглаживания в цикле производится усреднение высот 4 соседних пикселей. Для повешения качества и эффективности сглаживания, оно производится в 4 последовательных циклах – “слева направо”, “справа налево”, “сверху вниз” и “снизу вверх”.

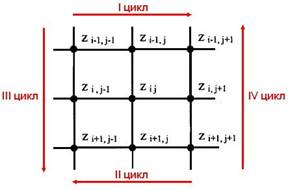
Рис. 2.1.2.1. Циклы сглаживания ландшафта

Пиксели для усреднения высот выбираются следующим образом: на K-ой итерации цикла производится усреднение высот пикселей с индексами (i – 1, j - 1), (i – 1, j), (i, j - 1) и (i, j), на (K + 1)-ой же, в зависимости от номера цикла, усредняются высоты следующих пикселей:

·        в I цикле – пиксели тех же двух строк с индексами столбцов, увеличенными на 1;

·        во II цикле – пиксели тех же двух строк с индексами столбцов, уменьшенными на 1;

·        в III цикле – пиксели тех же столбцов со строчными индексами, увеличенными на 1;

·        в IV цикле – пиксели тех же столбцов со строчными индексами, уменьшенными на 1.

Ниже приведена иллюстрация, демонстрирующая результаты сглаживания тестового ландшафта:

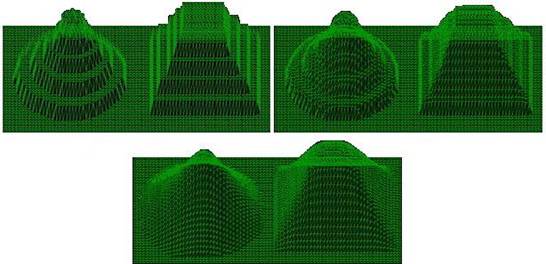
Рис. 2.1.2.2. Результаты сглаживания – без сглаживания, 1 цикл, 10 циклов.

2.1.3 Трехмерные аффинные преобразования

В процессе работы программы может возникать необходимость преобразования объектов сцены – их сдвига, масштабирования, поворота.

Для трехмерного пространства любое аффинное преобразование может быть представлено последовательностью простейших операций [3].

Ниже приводятся уравнения и матрицы преобразований:

·        сдвиг точки вдоль координатных осей на dx, dy, dz:

;

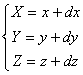
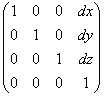·        масштабирование относительно начала координат с коэффициентами k_x, k_y, k_z:

;

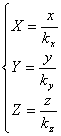
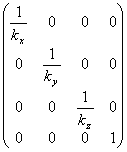·        поворот относительно осей x, y, z на угол :

o        ось x:

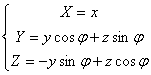
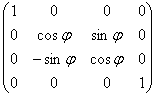
o        ось y:

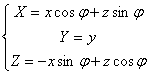
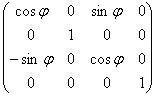
o     ось z:

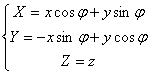
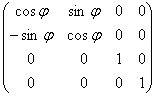
2.1.4 Проецирование

В настоящее время наиболее распространены устройства отображения, которые синтезируют изображение на плоскости, например – экране монитора. Устройства, которые создают по-настоящему объемные изображения, пока достаточно редки. Но все чаще появляются сведения о подобных разработках, например, об объемных мониторах [2].

При использовании графических устройств обычно используют проекции. Проекция задает способ отображения объекта на графическом устройстве.

При отображении пространственных объектов на экране необходимо знать координаты объектов. Рассмотрим две системы координат. Первая – мировые координаты, которые описывают истинное положение объектов в пространстве с заданной точностью. Другая – экранная система координат – система координат монитора, на экран которого осуществляется вывод изображения.

Пусть мировые координаты будут трехмерными декартовыми координатами. Для синтеза изображения на плоскости достаточно, казалось бы, двумерной экранной системы координат, однако из-за использования алгоритма Z-буфера (этот алгоритм будет описан далее), они должны быть трехмерными.

В компьютерной графике распространены параллельная и центральная (перспективная) проекции.

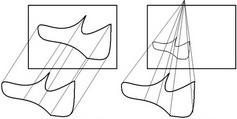
Рис. 2.1.4.1. Параллельная и центральная проекции

Для центральной проекции лучи проецирования исходят из одной точки, размещенной на конечном расстоянии от объектов и плоскости проецирования. Для параллельной проекции лучи проецирования параллельны.

В данной работе для визуализации сцены использовалась аксонометрическая (разновидность параллельной) проекция, для нее все лучи располагаются под прямым углом к плоскости проецирования.

Как правило, расположение плоскости проецирования задается с помощью двух углов - и .

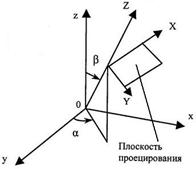
Рис. 2.1.4.2. Аксонометрическая проекция

Для того, чтобы найти соотношения между координатами (x, y, z) и (X, Y, Z) для любой точки в трехмерном пространстве, рассмотрим преобразование системы координат (x, y, z) в систему (X, Y, Z). Такое преобразование может быть задано двумя шагами:

·        поворот системы координат относительно оси z на угол . Такой поворот описывается матрицей

;

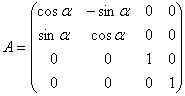·        поворот новой системы координат (x, y, z) относительно оси x на угол  - получение координаты (X, Y, Z). Матрица поворота:

.

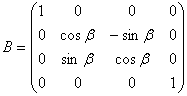Преобразование координат выражается произведением матриц

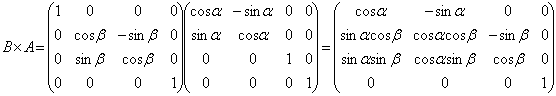
Это же преобразование можно записать в формульном виде:

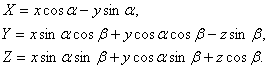
Похожие работы

Графические редакторы, используемые для создания векторных и растровых изображений

Скачать

24360

0

0

... средств. К примеру, Adobe Photoshop сейчас не является чисто растровым редактором, a CorelDRAW имеет довольно развитые средства работы с растровой графикой. 2. Графические редакторы, используемые для создания векторных и растровых изображений Редакторы растровой графики Microsoft Paint - простой (или лучше сказать - простейший) редактор, входящий в стандартную поставку операционных систем ...

Формирование изображения в телевизионных системах

Скачать

24268

0

3

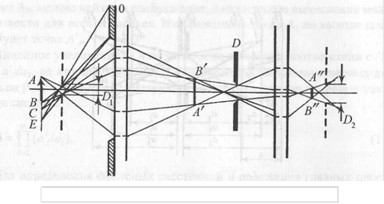
... поле зрения оптической системы. Положим, что D (рис.3) - действительная диафрагма, которая ограничивает пучок световых лучей, участвующих в формировании изображения, - апертурная диафрагма, DxuD2 - изображения этой диафрагмы в передней и задней частях оптической системы. Если Dy или D2 заменить реальными диафрагмами, то они будут ограничивать световой поток так же, как диафрагма D. На основании ...

Соотношение слова и изображения в комплексном аудиолингвовизуальном сообщении

Скачать

99490

3

0

... стало очень динамичным, разномасштабным, многоракурсным и цветовым, вследствие чего значительно возросла информационная насыщенность зрительного ряда. Глава 3. Соотношение слова и изображения в аудиовизуальном сообщении 1. Комплексное аудиолингвовизуальное сообщение Изображение как знаковая система первична по отношению к символическим знакам, в том числе и к написанному слову1. Первоначально ...

Искусство Германии 16 века

Скачать

96923

0

0

... после «Четырех апостолов» тоже не создал ничего значительного. Он скончался через два года после завершения этой работы — в 1528 году. Творчество Дюрера не имело непосредственных продолжателей, но его влияние на искусство Германии было огромным, решающим. Художники одного с ним поколения, так же как и его младшие современники, уже совсем иными глазами смотрели на мир, нежели мастера 15 в. Острый ...