Анализ методов Гуро и Фонга

2.1.7.4 Анализ методов Гуро и Фонга

Метод Фонга сложнее, чем метод Гуро. Для каждого пикселя поверхности необходимо выполнять намного больше вычислительных операций. Тем не менее, он дает лучшие результаты, в особенности при имитации зеркальных поверхностей.

Общие черты и отличия методов Фонга и Гуро можно показать на примере цилиндрической поверхности, аппроксимированной многогранником. Пусть источник света находится за нами. Проанализируем закрашивание боковых граней.

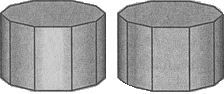
Рис. 2.1.7.4.1. Отличия закрашивания Фонга и Гуро

Ребра граней показаны черным цветом для иллюстрации особенностей закрашивания, на самом деле после закрашивания никакого каркаса не будет, и поверхность будет выглядеть гладкой.

Основные отличия заметны на передней грани. Она перпендикулярна направлению лучей света, поэтому нормали в вершинах этой грани располагаются симметрично – они образуют попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обусловливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность остается постоянной. Это обусловливает единый цвет закрашивания, а это, очевидно, неправильно.

Метод Фонга дает правильное закрашивание. Если интерполировать нормали передней грани, то по центру будут интерполированные нормали, параллельные лучам света. Поэтому центр передней грани будет светлее, чем края.

2.1.8 Последовательность действий при визуализации сцены

План действий, необходимых для визуализации сцены приведен на следующей схеме:

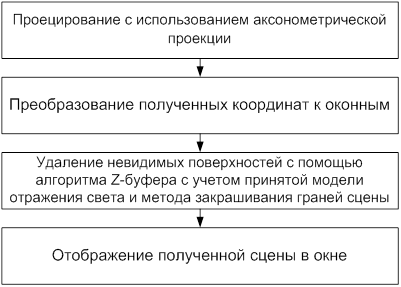
Рис. 2.1.8.1. Схема визуализации сцены

2.2 Типы, структуры данных и функции, использованные при реализации программного комплекса

2.2.1 Представление исходных данных

При проектировании программы важно сразу решить, как будут представлены исходные данные, то есть, в условиях данной работы – как будет описана карта изообластей высот и трехмерный ландшафт, какими будут форматы файлов для хранения информации о карте и ландшафте.

В данной работе был выбран полигональный способ аппроксимации пространственных фигур. Сущность полигональной модели состоит в том, что каждое тело представляется в виде определенного набора граней-многоугольников, с определенной точностью приближающих форму исходного тела. В качестве грани-многоугольника был выбран треугольник, так как это наиболее простой многоугольник, его точки всегда лежат в одной плоскости и любой более сложный многоугольник можно разбить на несколько треугольников.

Разработанные типы данных и форматы файлов подробно описаны в последующих разделах.

2.2.2 Программа «Редактор карт»

2.2.2.1 Изообласти высоты

Изообласть характеризуется цветом и высотой, поэтому для хранения информации о каждом типе изообластей используется следующая запись:

THeightColor = record

 Color : TRGBColor;

 Height : Single;

 end;

Поля этой записи имеют следующее значение:

·        Color – цвет изообласти;

·        Height – представляемая высота.

Размер записи – 8 байт (компилятор Delphi производит выравнивание полей в записи, поэтому размер записи оказывается равным 8 байтам, а не 7, как должно быть).

Тип TRGBColor используется для хранения RGB-цвета. Представим его структуру:

TRGBColor = record

 R, G, B : Byte;

 end;

Размер записи – 3 байта (по неизвестным причинам в этом случае выравнивания не произошло).

В процессе создания каждой карты создается динамический массив, для хранения информации обо всех типах изообластей:

THeightColors = array of THeightColor;

2.2.2.2 Равномерная сетка высот и ландшафт

Для хранения узлов исходной равномерной сетки (с шагом 1) используется динамический массив элементов типа Single:

TZBitMap = array of array of Single;

Тип Single использован для экономии оперативной памяти и дискового пространства, точность этого типа – 8 знаков после запятой, что вполне достаточно в рамках этой работы, при этом переменная этого типа занимает в памяти 4 байта, вдвое меньше, чем переменная типа Real.

При триангуляции равномерной сетки создается динамический массив треугольников ландшафта. Для хранения информации о треугольнике используется следующий тип данных:

TTriangle = record

 P : array [0..2] of TPoint3

 N : TPoint3

 pD : Single;

 aN : array [0..2] of TPoint3;

 Color : TRGBColor;

 end;

Поля этой записи имеют следующие значения:

·        P – массив точек треугольника;

·        N – нормаль к плоскости треугольника;

·        pD – свободный член уравнения плоскости, несущей треугольник;

·        aN – массив усредненных нормалей в вершинах треугольника;

·        Color – базовый цвет треугольника.

Поля N и pD в совокупности образуют уравнение плоскости, несущей треугольник.

Размер записи – 92 байта (реальный размер, без выравнивания – 91 байт).

Необходимо привести описания типов, использованных в записи TTriangle:

TPoint3 = record

 X, Y, Z : Single;

 end; - запись служит для хранения координат точки.

Размер записи – 12 байт.

Для работы с равномерной сеткой высот предусмотрены следующие процедуры и функции:

·        function CreateZBitMap(Width, Height : Integer) : TZBitMap – выделение памяти для первичной сетки высот, ее размеры - Width и Height, совпадают с размерами области вывода;

·        procedure FreeZBitMap(var ZBMP : TZBitMap) – освобождение памяти, занимаемой первичной сеткой высот;

·        function FillZBitMap(Image : TImage; Colors : THeightColors) : TZBitMap - заполнение первичной сетки высот на основе изображения, хранимого в Image и соответствий «Цвет-высота», содержащихся в массиве Colors;

·        function DivideZBitMapIntoTriangles(BitMap : TZBitMap; StepX, StepY : Integer) : TTriangles – функция преобразования первичной равномерной сетки BitMap в более разреженную сетку с шагами StepX и StepY по горизонтали и вертикали соответственно. После этого преобразования полученная сетка разбивается на треугольники, на основе которых будет построен ландшафт;

·        procedure SmoothMap(var BitMap : TZBitMap) – процедура для проведения одного цикла сглаживания первичной сетки высот;

Для работы с треугольниками ландшафта предназначены следующие процедуры:

·        procedure FillTrianglesNormals(var Triangles : TTriangles) – расчет и заполнение всех полей записи TTriangle, кроме координат точек и цвета;

В процедуре FillTrianglesNormals используются следующие вспомогательные функции:

·        function GetNormal(T : TTriangle) : TPoint3 – процедура для вычисления координат вектора нормали к плоскости треугольника;

·        function CorrectNormal(N : TPoint3) : TPoint3 – процедура нормализации вектора нормали;

·        procedure AddNormal(var N : TPoint3; NAdd : TPoint3; var Count : Integer), procedure DivideNormal(var N : TPoint3; Count : Integer) – эти процедуры в совокупности служат для вычисления усредненной нормали в вершине треугольника;

Похожие работы

Графические редакторы, используемые для создания векторных и растровых изображений

Скачать

24360

0

0

... средств. К примеру, Adobe Photoshop сейчас не является чисто растровым редактором, a CorelDRAW имеет довольно развитые средства работы с растровой графикой. 2. Графические редакторы, используемые для создания векторных и растровых изображений Редакторы растровой графики Microsoft Paint - простой (или лучше сказать - простейший) редактор, входящий в стандартную поставку операционных систем ...

Формирование изображения в телевизионных системах

Скачать

24268

0

3

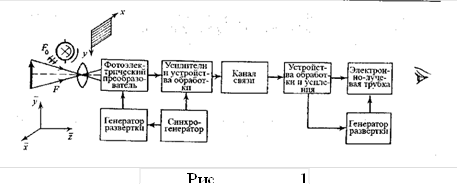
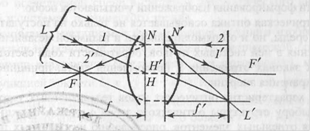
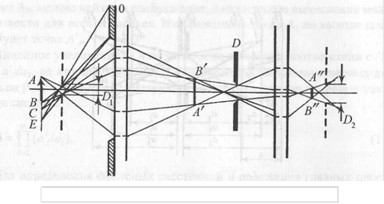
... поле зрения оптической системы. Положим, что D (рис.3) - действительная диафрагма, которая ограничивает пучок световых лучей, участвующих в формировании изображения, - апертурная диафрагма, DxuD2 - изображения этой диафрагмы в передней и задней частях оптической системы. Если Dy или D2 заменить реальными диафрагмами, то они будут ограничивать световой поток так же, как диафрагма D. На основании ...

Соотношение слова и изображения в комплексном аудиолингвовизуальном сообщении

Скачать

99490

3

0

... стало очень динамичным, разномасштабным, многоракурсным и цветовым, вследствие чего значительно возросла информационная насыщенность зрительного ряда. Глава 3. Соотношение слова и изображения в аудиовизуальном сообщении 1. Комплексное аудиолингвовизуальное сообщение Изображение как знаковая система первична по отношению к символическим знакам, в том числе и к написанному слову1. Первоначально ...

Искусство Германии 16 века

Скачать

96923

0

0

... после «Четырех апостолов» тоже не создал ничего значительного. Он скончался через два года после завершения этой работы — в 1528 году. Творчество Дюрера не имело непосредственных продолжателей, но его влияние на искусство Германии было огромным, решающим. Художники одного с ним поколения, так же как и его младшие современники, уже совсем иными глазами смотрели на мир, нежели мастера 15 в. Острый ...