Постановка завдання яке буде виконане у курсовій роботі

3. Постановка завдання яке буде виконане у курсовій роботі

Розглянемо систему, яку можна в будь-який момент часу можна описати одним з N станів, S₁, S₂,...S_N, (мал. 1), де для простоти N = 5. Через певний проміжок часу система може змінити свій стан або залишитися в колишньому стані відповідно до ймовірностям, зазначеним для цих станів. Моменти часу, коли ми реєструємо стан системи ми позначимо як t=1,2,... , а стан в момент часу t - ми позначимо _q t. Повний опис розглянутої вище системи, повинно містити поточний стан (в момент часу t) і послідовність всіх попередніх станів, через які пройшла система. В окремих випадках опис системи зводиться до вказівкою поточного та попереднього стану.

 (1)

Крім того, ми також вважаємо що процеси, що протікають у системі, не залежать від часу, про що нам говорить права частина формули (1). Таким чином, систему можна описати безліччю ймовірностей a i j у вигляді

  (2)

де _a i j - це ймовірність переходу з стану _S i в стан _S j в даний момент часу. Оскільки ці ймовірності характеризують випадковий процес, вони мають звичайні властивості, т. е.

 (3.1)

 (3.2)

Описаний вище випадковий процес можна назвати відкритою марківською моделю, оскільки вихідний сигнал моделі - це послідовність станів реєструються в часі. Кожен стан відповідає певному (що спостерігається) події. Для того, щоб краще зрозуміти все вищесказане, розглянемо просту марківську модель погоди, у якій буде всього три стану. Передбачається, що ми один раз на день (наприклад, в опівдні), дивимося у вікно і реєструємо в журналі поточний стан погоди. Ми домовилися, що лише один із трьох нижче названих станів в день t ми записуємо в журнал:

-    Стан № 1: дощ (або сніг)

-    Стан № 2: хмарно, можливий дощ

-    Стан № 3: ясно

Матриця ймовірностей зміни погоди A має вигляд

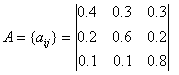
Виходячи з того, що погода в перший день (t = 1) ясна (стан 3), ми можемо задати собі питання: яка вірогідність (згідно з нашою моделі), що наступні 7 днів буде саме «зрозуміло - ясно - дощ - дощ - ясно - Хмарно, можливий дощ - ясно »? Точніше сказати, для цієї послідовності станів O, де  відповідає, t=1,2,...,8, Ми хочемо на основі даної моделі визначити ймовірність спостереження послідовності O. Ця ймовірність може бути виражена (і обчислено) наступним чином

  (4)

це ймовірність того, що початковий стан системи буде Si.

Є й інший цікаве питання, відповідь на яке нам дасть ця модель: яка вірогідність того, що модель збереже свій стан протягом рівно d днів? Ця ймовірність може бути обчислено як ймовірність спостереження такій послідовності

дає модель, в якій

 (5)

Величина pi (d) - це ймовірність того, що система буде перебувати в стані i рівно d раз поспіль. Відповідно є функція розподілу ймовірності для тривалості перебування системи в одному стані, яка є характеристикою збереження стану для марківських ланцюга. Знаючи величини pi (d) ми можемо обчислити середній час, протягом якого система збереже свій стан (використовуємо формулу математичного очікування):

 (6.1)

 (6.2)

Очікується, що сонячна погода швидше за все простоїть 5 днів, похмура - 2,5 дні, а от дощова погода, згідно з нашою моделі, імовірніше за все протримається 1,67 дня.

4. Існуючі шляхи вирішення задачі

У описаної марківській моделі кожній фізичній явищу відповідало певний стан моделі. Ця модель, на жаль, занадто обмежена, і їй не під силу рішення багатьох актуальних проблем. У цьому розділі ми розглянемо марківські моделі, у яких спостерігаються послідовність - це результат переходів у відповідності з позначеними ймовірностей. У даному випадку модель (прихована марківська модель) - це результат двох випадкових процесів. Перший - прихований процес - його ніяк не можна зареєструвати, але його можна охарактеризувати за допомогою іншого випадкового процесу, який надає нам набір сигналів - спостерігається послідовність. Проілюструємо цей опис на прикладі підкидання монети.

Приклад монети, яку підкидають. Ви знаходитесь в кімнаті, а за перегородкою - в іншій кімнаті - знаходиться людина, яка підкидає монету. Він не говорить, як саме він підкидає монету, а може він її взагалі лінується підкидали. Він лише говорить вам результат кожного падіння монети: орел чи решка. У цьому й полягає суть прихованого процесу (ви не знаєте, що відбувається з монетою), коли про процесі ви можете судити лише за що спостерігається послідовності

,

де Н - це орел, а Т - це решка.

Як же побудувати приховану марківську модель, що відповідає цій ситуації? Перше питання: скільки станів буде у моделі і що означає кожне стан такої моделі? Припустимо, що ми підкидаємо одну єдину монету, а інших у нас немає. Тоді вибір ми зупинимо на моделі з двома станами, де одне стан означає випадання орла, інше - решка. [1]

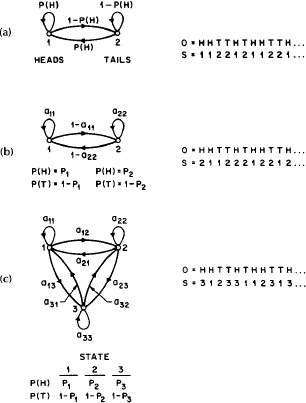
мал. 2.

Три марківські моделі, які можуть описати експеримент з монетою, що підкидається. (а) 1 монета бере участь у підкиданні, (2) 2 - монети, (3) - три монети.

Ця модель зображена на малюнку 2 (а). У цьому випадку марківських модель є відкритою і єдине, що ми можемо зробити з цією моделлю - це оптимізувати ймовірність зміни стану. Слід зауважити, що прихована марківських модель, що є аналогом моделі, зображеної на рис. 2 (а), буде представляти собою модель одного стану. В цій моделі єдине стан означає, що підкидана всього лише одна монета.

На наступному малюнку 2 (б) зображена ПММ двох станів. У цьому випадку кожне стан відповідає різним монетам, які підкидають в ході експерименту (наприклад, 1 копійка і 5 рублів). Кожному станом відповідає розподіл ймовірностей між випаданням орла і решка, а також матрицею ймовірностей переходів (матрицею переходів), що вказує ймовірність переходу з одного стану в інше. Перехід зі стану в стан згідно з заданим ймовірностям з матриці переходів може здійснюється на основі того ж підкидання монети або на основі будь-якої іншої випадкової події.

На третьому малюнку 2 (в) представлена модель, що враховує той факт, що підкидають три різні монети, причому вибір між ними здійснюється знову ж таки на основі якого-небудь випадкового події.

Тут, як і кожен раз при проектуванні ми задаємося питанням: яка з трьох моделей найкращим чином підходить для опису, що спостерігається послідовності? Добре видно, що перша модель (мал. 2 (а)) має всього лише 1 невідомий параметрМодель для двох монет (мал. 2 (б)) має 4 невідомих параметра І нарешті, модель для трьох монет (мал. 3 (в)) має 9 невідомих параметрів. Таким чином, ПММ з великою кількістю ступенів свободи по суті більш дієздатна, ніж її менші аналоги. Також теоретично доведено (і це ми побачимо далі), що в сучасних умовах існують обмеження на розмір моделей. Більш того, може виявитися, що у випадку, коли людина за стіною підкидає одну єдину монету, ми виберемо модель трьох станів. У такому випадку з'ясовується, що стану системи не відповідають реальним станів за стіною, і, отже, ми використовуємо надлишкову модель.

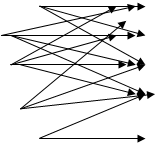
Приклад кульок у вазах. Зараз ми доповнимо ПММ новими структурними елементами, для того, щоб вона могла вирішувати ряд більш складних завдань. Допоможе нам в цьому приклад з кульками у вазах (мал. 3).

мал. 3. Модель з N станами (вазами) та кульками, кольори яких позначають елементи що спостерігається послідовності.

Припустимо, у нас є N скляних прозорих ваз. У кожній вазі - велике число кульок різного кольоруВважаємо, що у нас в кошику лежать кульки M різних кольорів. Фізично це можна представити наступним чином. Людина знаходиться в кімнаті з вазами. Яким-небудь випадковим чином він вибирає будь-яку вазу, простягає руку глибше, і витягує м'яч. Колір кулі записується в журнал показань - спостерігається послідовність, і людина кладе шар назад в цю вазу. Потім наша людина вибирає нову вазу, і йде до неї, і витягує звідти новий шар, і так далі. В результаті ми отримуємо послідовність кольорів - результат роботи ПММ - спостерігається послідовність.

Очевидно, що приклад кульок у вазах відповідає прихованої марківській моделі, де кожне стан моделі - це обрана ваза, причому в різних ваз різну ймовірність витягти кульку червоного (або іншого) кольору, що відповідає різного розподілу ймовірностей для кожного стану. Те, яка ваза буде обрана наступної, залежить від матриці переходів ПММ, т. е. залежить і від того, у якої вази ми зараз знаходимося.[1]

Елементи прихованої марківської моделі

Наведені вище приклади дають непогане уявлення про ПММ, і про можливі сферах їх застосування. Зараз ми дамо формальне визначення елементів ПММ і зрозумілий, як модель генерує спостережувану послідовність. ПММ визначається наступними елементами:

1. N - загальна кількість станів в моделі. Незважаючи на те, що стану в ПММ є прихованими, у багатьох випадках є відповідність між станом моделі і реальним станом процесу. У прикладі з підкиданням монети кожне стан відповідно до обраної монеті, а в прикладі з кульками у вазах стан моделі відповідно до обраної вазі. В загальному, перехід у будь-який обраний стан можливий з будь-якого стану всієї системи (в тому числі й сама в себе); з іншого боку, і це ми побачимо згодом, лише певні шляхи переходів представляють інтерес у кожної конкретної моделі. Ми позначимо сукупність станів моделі безліччю , , a поточний стан в момент часу t як q.

2. M, кількість можливих символів у що спостерігається послідовності, розмір алфавіту послідовності. У випадку з підкиданням монети - це 2 символу: орел і решка; у випадку з кульками - це кількість кольорів цих самих кульок. Алфавіт що спостерігається в послідовності ми позначимо як .

3. Матриця ймовірностей переходів (або матриця переходів) , де

 ,  (7)

ттобто це ймовірність того, що система, що перебуває в стані Si, перейде в стан Sj. Якщо для будь-яких двох станів в моделі можливий перехід з одного стану в інше, то _a i j> 0 для будь-яких i, j. В інших ПММ для деяких i, j у нас ймовірність переходу _a i j = 0.

4. Розподіл ймовірностей появи символів у j-тому стані, , где , де

   (8)

b j (k) - імовірність того, що в момент часу t, система, яка знаходиться в j-му стані (стан Sj), видасть k-тий символ (символ k) в спостережувану послідовність.

5. Розподіл ймовірностей початкового стану , где , де

, , (9)

тобто ймовірність того, Si - це початковий стан моделі.

Сукупність значень N, M, A, B і π - це прихована марківська модель, яка може згенерувати послідовність

 (10)

(де O _t — один з символів алфавіту V , а T — це кількість елементів в послідовності.

ПММ будує спостережувану послідовність по наступному алгоритмі

1.         Вибираємо початковий стан q ₁ = S _i відповідно до розподілу π

2.         Встановлюємо t = 1 .

3.         Вибираємо O _t = v _k відповідно до розподілу b _j ( k ) у стані ( S _i ).

4.         Переводимо модель у новий стан q _{t + 1} = S _j відповідно до матриці переходів a _{i j} з урахуванням поточного стану S _i .