Навигация
Разработка программы для решения систем линейных уравнений
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАВТ
РАЗРАБОТКА ПРОГРАММЫ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Пояснительная записка
Курсовая работа по дисциплине
"Информатика"
ТПЖА.12203-01 81 01 ПЗ
Разработал студент гр. СК-00 ____________ /А. И. Иванов/
Руководитель преподаватель
ФАВТ ____________ / К. И. Петров/
Курсовая работа защищена с оценкой“___________” “__”_____2002 г.
Киров 2002
Реферат
А. И. Иванов. Разработка программы для решения систем линейных уравнений: ТПЖА 12203-01 81 01 ПЗ. Курсовая работа/ВятГУ, ФАВТ, рук. К. И. Петров – Киров, 2002. ПЗ 7 с., 3 табл., 8 рис., 4 источника, 4 прил.; програм. докум. 18 л.
СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ, МЕТОД ЗЕЙДЕЛЯ, МЕТОД ПРОСТЫХ ИТЕРАЦИЙ, МАТРИЦА КОЭФФИЦИЕНТОВ, ВЕКТОР СВОБОДНЫХ ЧЛЕНОВ, УСЛОВИЕ СХОДИМОСТИ
Объектом исследования являются итерационные методы решения систем линейных алгебраических уравнений (далее СЛАУ): метод простых итераций и метод Зейделя.
Цель работы – разработка программы для решения СЛАУ с произвольным количеством уравнений.
Для получения вектора решений СЛАУ реализованы методы Зейделя и простых итераций.
Недостатком исследуемого метода – невозможность нахождения решения за конечное число итераций даже при отсутствии вычислительной погрешности.
Результаты проведённой работы могут быть использованы при решении СЛАУ с произвольным количеством уравнений.
Среда программирования – Borland C.
Содержание
Введение 2
1 Анализ задания и выбор метода решения 3
1.1 Анализ задания 3
1.2 Выбор метода решения 3
1.2.1 Метод простых итераций 4
1.2.2 Метод Зейделя 4
2 Реализация метода решения задачи 5
2.1 Контроль входной информации 5
2.2 Формат вывода выходной информации 5
2.3 Выбор типов входных, рабочих и выходных переменных,
используемых в программе 6
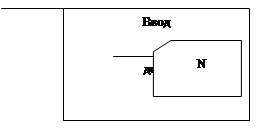
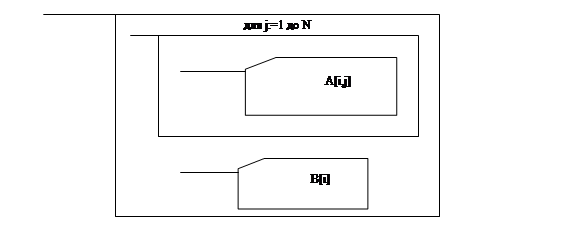
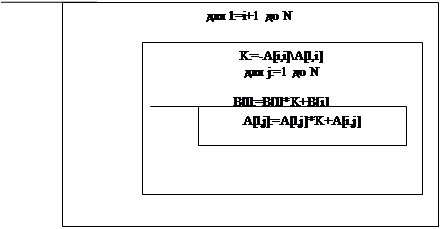
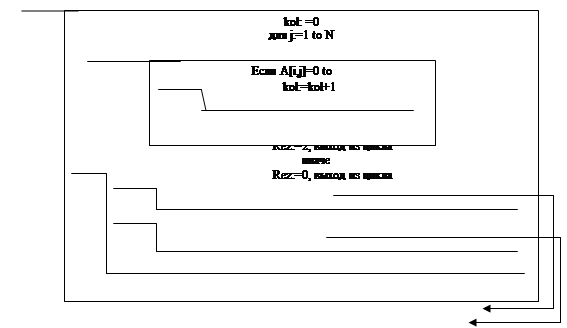
2.4 Проектирование программы 6
2.5 Анализ результата 6
Заключение 7
Приложение А (обязательное) Разработка программы для решения систем линейных уравнений. Описание программы. ТПЖА.12203-01 13 01 8
Приложение Б (обязательное). Разработка программы для решения систем линейных уравнений. Руководство пользователя. ТПЖА.12203-01 34 01..
Приложение В (обязательное). Разработка программы для решения систем линейных уравнений. Текст программы. ТПЖА.12203-01 12 01 23
Приложение Г (справочное) 45
Введение
Решение СЛАУ является одной из важных вычислительных задач, часто встречающихся в прикладной математике. К решению систем линейных уравнений сводится ряд задач анализа, связанных с приближением функций, решение систем дифференциальных уравнений и интегральных уравнений и т.д.
В связи с использованием большого количества переменных в системе ручной расчёт СЛАУ довольно трудоёмкий и может занять много времени. Актуальность данной курсовой работы заключается в том, что вышеописанная проблема разрешается с помощью разработанной курсовой программы.
Курсовая работа носит учебный характер. В ходе её программист реализовал имеющиеся знания из курса линейной алгебры по решению СЛАУ в программной интерпретации на языке программирования С. А знание компьютера и наличие опыта в программировании в наше время особенно приветствуется в фирмах, работающих в сфере информационных технологий.
1 Анализ задания и выбор метода решения
1.1 Анализ задания
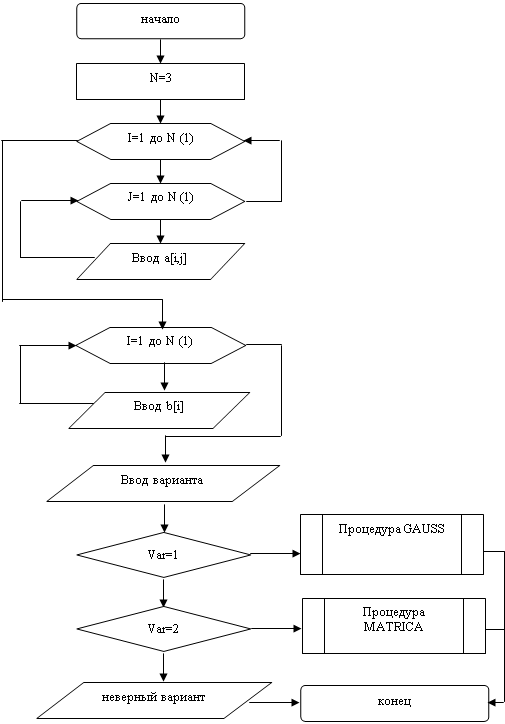
В соответствии с заданием на курсовую работу необходимо разработать программу для решения СЛАУ методом простых итераций и методом Зейделя. Предусмотреть ввод числа уравнений, матрицы коэффициентов и вектора свободных членов, а также вывод вектора решений на экран.
Для удобства тестирования программа должна обладать понятным и логичным интерфейсом, рассчитанным на неопытного пользователя.
1.2 Выбор метода решения
В соответствии с заданием на курсовую работу в программе реализованы итерационные методы: простых итераций и Зейделя.
Пусть ищется решение невырожденной системы уравнений[1]
.
(1)
Первым шагом в итерационном методе является преобразование исходной системы к виду[1]
,
(2)
где матрицы С, В и вектор d определяются по матрицы А и вектору b. Причём системы (1) и (2) являются эквивалентными, т.е. их решения совпадают, а построение обратной матрицы С-1 проще, чем А-1. [1]
Вторым шагом является расстановка индексов или номеров приближений в (2) и задание нулевого приближения. Например,
(3)
где - заданный вектор [1]
Третьим шагом итерационного метода является обоснование сходимости последовательных приближений , полученных из (3), к точному решению х системы и оценка погрешности k-го приближения[1]
(4)
Оценка (4) при заданном позволяет остановить итерационный про-цесс (3). [1]
Различные итерационные методы отличаются первыми двумя шагами, а выбор конкретного метода должен производиться на основании оценки(4). [1]
1.2.1 Метод простых итераций
В методе простых итераций матрица С (2) выбирается единичной: С=Е. Итерационный процесс описывается формулой
(5)
где - заданный вектор. [1]
1.2.2 Метод Зейделя
Отличие метода Зейделя от простой итерации состоит лишь в том, что при вычислении (k+1)-го приближения полученные компоненты вектора сразу же используются в вычислениях. В матричной записи это можно представить так:
где матрицы U и L получены разложением В в сумму:
матрица U – верхняя треугольная часть B, включая диагональ; L – нижняя поддиагональная часть В. [1]
Таким образом метод Зейделя можно записать в следующей форме
(6)
Заметим, что построение матрицы, обратной , не представляет труда, так как это нижняя треугольная матрица. [1]
2 Реализация метода решения задачи
2.1 Контроль входной информации
Метод контроля входной информации должен обеспечить максималь-ную защиту от некорректности вводимых данных, защиту от переполнения строки и минимальный перечень ограничений при вводе информации.
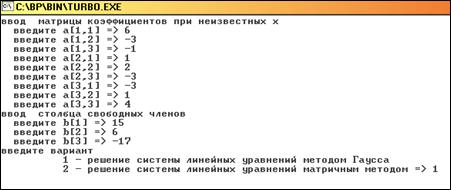
В программе входные данные, задаются пользователем в режиме диалогового окна. Это позволяет практически полностью контролировать входную информацию и избежать некорректности вводимых данных, так как далее эта информация используется в вычислениях. Функции float_input() и n_input() предназначены для защиты от некорректного ввода действительных и натуральных чисел соответственно (приложение В).
2.2 Формат вывода выходной информации
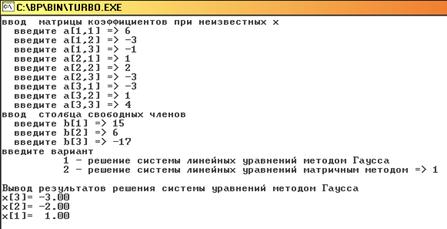
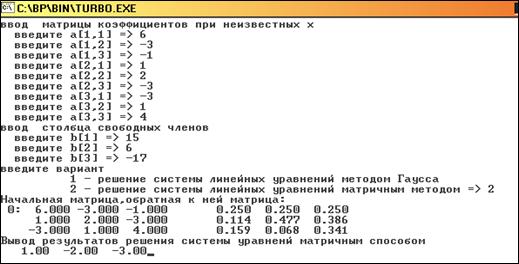
Вывод результатов расчёта производится в окне Output.
В окне выводится исходная СЛАУ, ниже вектор решений, а также число итераций, необходимых для нахождения решения.
2.3 Выбор типов входных, рабочих и выходных переменных, используемых в программе
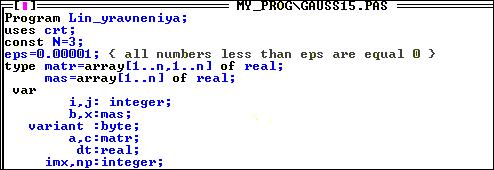
В программе использованы следующие переменные:
char ch
int s
int n
double **A
double *B
double *X
bool inpflag=false
bool decflag=false
перемещение между окнами
число итераций
размерность матриц
матрица коэффициентов
вектор свободных членов
вектор решений
флажок выполнения операции ввода
флажок выполнения операции решения
Похожие работы
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
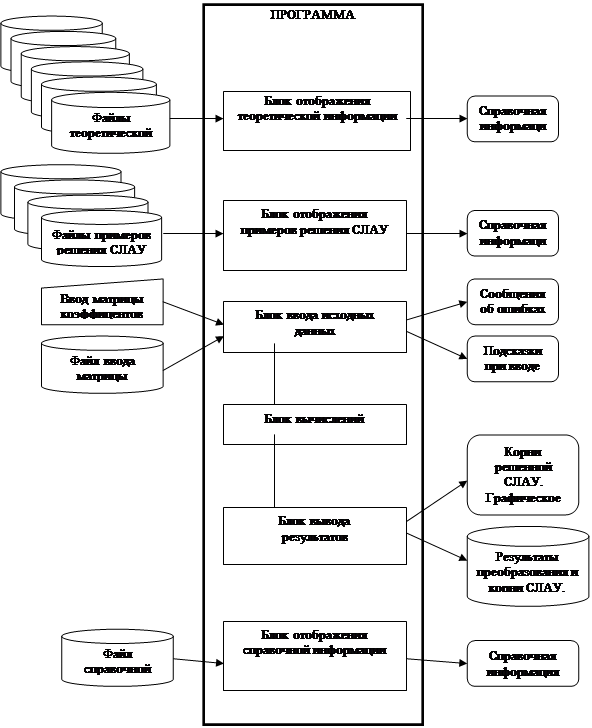
... Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса Условные обозначения к рисунку 2.1: - данные, вводимые с клавиатуры - данные, хранящиеся на диске - данные, выводимые на экран 2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными ...
... строке матрицы i2-ю, умноженную на число r; процедура MultMatr предназначена для умножения матриц. Функция Sign используется для изменения знака на противоположный при вычислении обратной матрицы. Программа настроена на решение системы 3-х линейных уравнений с тремя неизвестными. Чтобы решить систему из 2-х уравнений с 2-мя неизвестными необходимо в программе изменить значение константы N с ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...

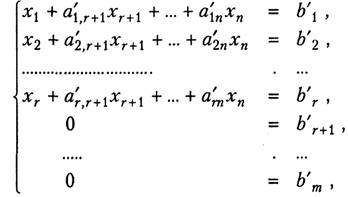

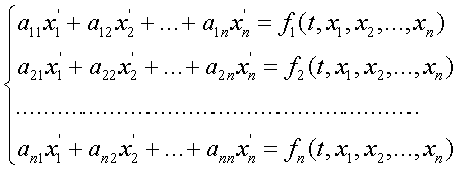
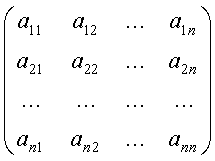
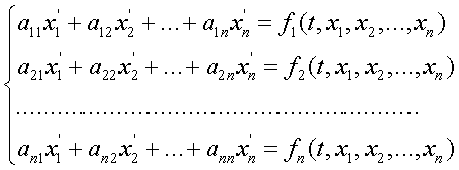
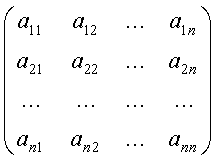
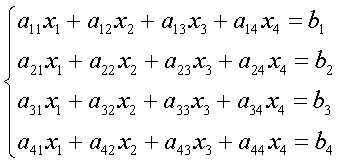
0 комментариев