Навигация
2.4 Проектирование программы
Рабочий модуль программы – Zeidel.cpp.
Для корректной работы программы реализованы методы корректного ввода входной информации, решение СЛАУ с пояснением выполняемых действий, форматированный вывод выходной информации на экран и в файл. Для удобства тестирования разработан интерфейс, рассчитанный на неопытного пользователя.
2.5 Анализ результата
В результате проделанной программистом работы разработана программа, реализующая решение СЛАУ методами Зейделя и простых итераций и выполненная в удобном и понятном интерфейсе, понятном неопытному пользователю.
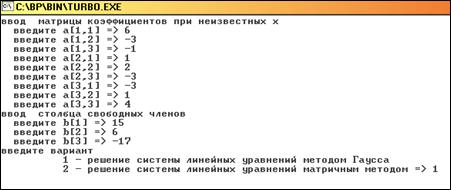
Пример расчета СЛАУ со следующими входными данными:
Исходная матрица А 45 8.6
7.3 8.1
Вектор свободных членов В 12
4.5
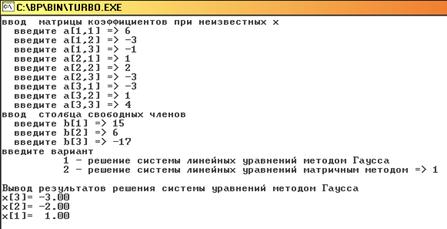
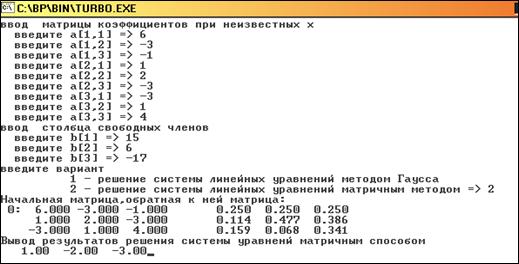
Результаты расчёта:
Вектор решений 0.1938
0.3809
Число итераций 5
Заключение
В ходе курсовой работы был разработан программный продукт, в рамках которого были реализованы:
метод простых итераций для решения СЛАУ;
метод Зейделя для решения СЛАУ;
удобный оконный интерфейс для неопытного оператора;
защита от неправильного ввода входной информации;
Приложение А
(обязательное)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАВТ
РАЗРАБОТКА ПРОГРАММЫ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
ОПИСАНИЕ ПРОГРАММЫ
Лист утверждения
ТПЖА.12203-01 13 01-ЛУ
Листов 2
Разработал студент гр. СК-00 ____________ / А. И. Иванов /
Руководитель преподаватель
ФАВТ ____________ / К. И. Петров/
Киров 2002
Приложение А
(обязательное)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАВТ
Лист утверждения
ТПЖА.12203-01 13 01-ЛУ
РАЗРАБОТКА ПРОГРАММЫ ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
ОПИСАНИЕ ПРОГРАММЫ
ТПЖА.12203-01 13 01
Листов 8
Киров 2002
Аннотация
В разделе «Описание программы» рассмотрены функциональные характеристики программы. Перечислены требуемые технические средства для её нормальной работы, а также входные и выходные данные. Приведены необходимые схемы алгоритмов.
Содержание
1 Общие сведения 12
2 Состав и структура программного модуля 12
3 Описание логической структуры 13
4 Входные данные 14
5 Выходные данные 14
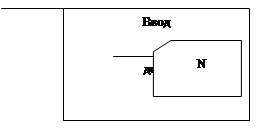
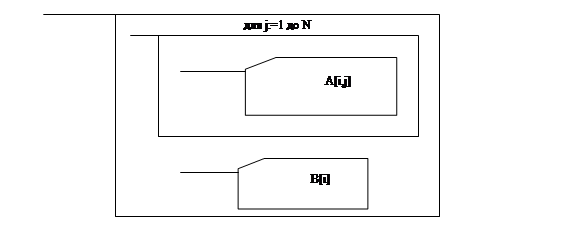
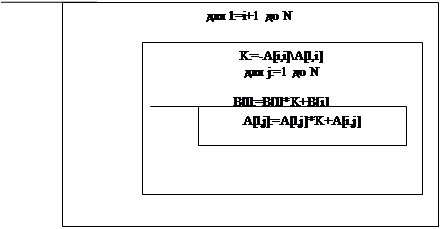
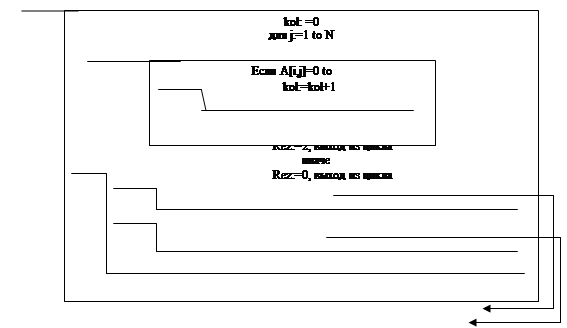
6 Схемы алгоритмов программы 15
1 Общие сведения
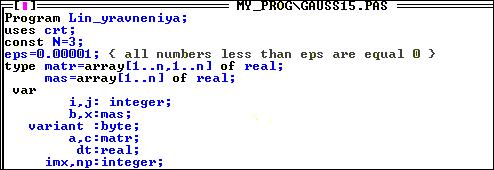
Исходный текст программы написан на языке С.
2 Состав и структура программного модуля
Программный код представлен в модуле Zeidel.cpp, состав которого представлен в таблице А.1.
Таблица А.1 – Состав программного модуля Zeidel.cpp
Функция Назначение
main Основная функция программы
input Ввод исходных данных
float_input Ввод действительных чисел
n_input Ввод натуральных чисел
decision Решение СЛАУ
output Вывод результата работы программы
menu Функция рисования пунктов меню
help Вывод на экран информации о программе и разработ-чике
cursor Навигация курсора
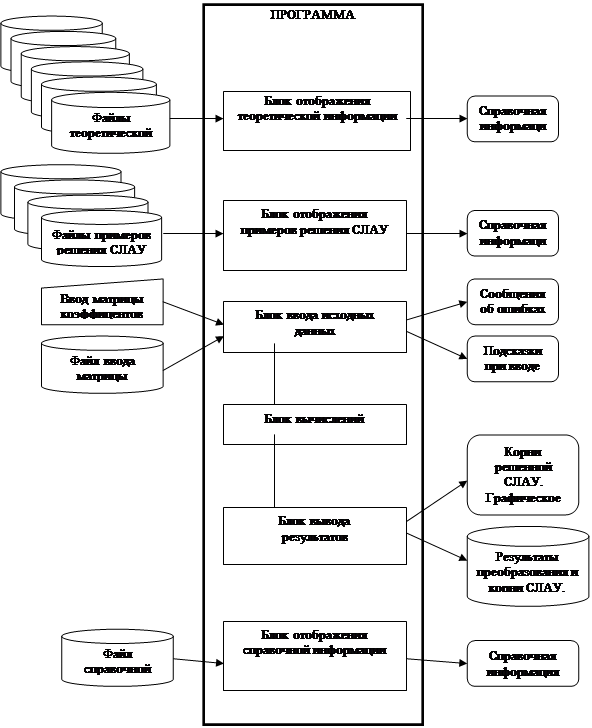
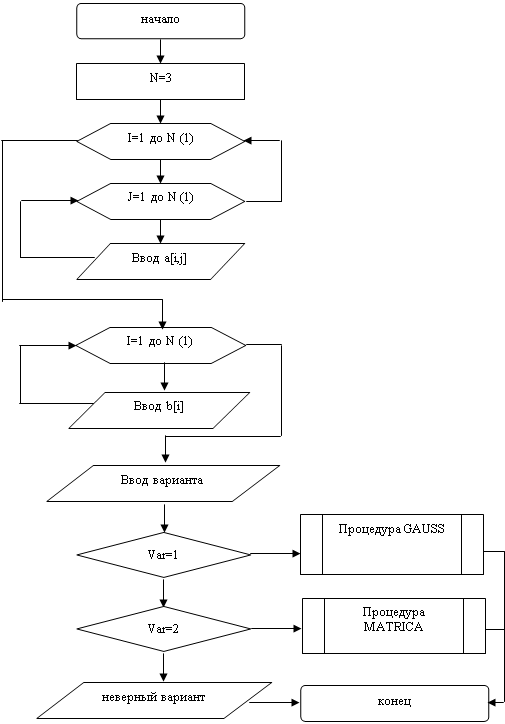
Данный программный продукт имеет структуру, представленную на рисунке А.1.
Рисунок А.1 – Структура программного модуля
3 Описание логической структуры
Функция main – основная функция программы, реализующая меню для выбора требуемой операции. Тело функции представляет собой цикл, в котором производится вывод строк меню, ожидание ввода символа с клавиатуры и последующий анализ введенного символа.
Навигация в меню осуществляется клавишами курсора. И в соответствии с выбранным пунктом открывается диалоговое окно.
Функция menu играет связующее звено в интерфейсе программы – вы-водит на экран меню программы.
Ввод данных производится функцией input, а проверка корректности вводимой информации функциями float_input, которая позволяет вводить действительные числа, и n_input, позволяющая вводить натуральные числа, а также ограничивает ввод цифр в числе и препятствует вводу иных символов.
Решение введенной СЛАУ реализовано в функции decision. При этом пользователю предлагается выбор метода решения СЛАУ (метод Зейделя или
метод простых итераций).
Вывод результатов производится функцией output на экран.
В случае выбора опций «Decision» и «Output» без выполнения опции «Input» и опции «Output» без «Decision» программа выдаст предупредительное сообщение с напоминанием выполнения требуемых действий.
3 Входные данные
Входные данные представлены в таблице A.2.
Таблица А.2 – Входные данные
Переменная Диапазон Назначение
int n 1…10 Размерность матриц
double **А -99.99…99.999 Матрица коэффициентов
double *В Вектор свободных членов
Похожие работы
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
... Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса Условные обозначения к рисунку 2.1: - данные, вводимые с клавиатуры - данные, хранящиеся на диске - данные, выводимые на экран 2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными ...
... строке матрицы i2-ю, умноженную на число r; процедура MultMatr предназначена для умножения матриц. Функция Sign используется для изменения знака на противоположный при вычислении обратной матрицы. Программа настроена на решение системы 3-х линейных уравнений с тремя неизвестными. Чтобы решить систему из 2-х уравнений с 2-мя неизвестными необходимо в программе изменить значение константы N с ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...

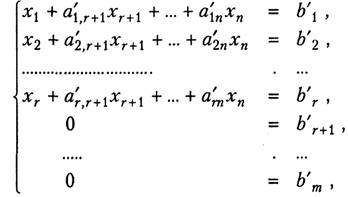

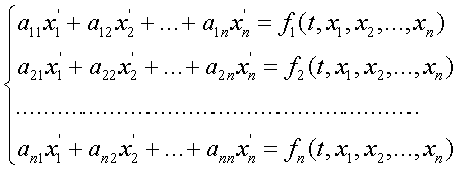
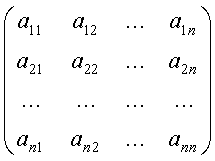
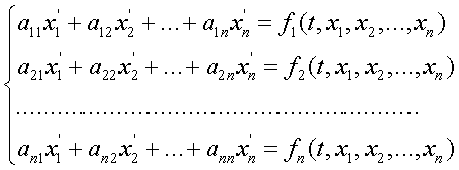
0 комментариев