Навигация
1.3 Задача № 1.84
Дискретный источник выбирает сообщения из ансамбля
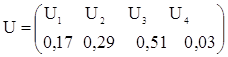 .
.
Длительности сообщений соответственно равны: tu1=0,96 c, tu2=0,44 c, tu3=0,67 c, tu4=0,39 c. Определить производительность источника.
Решение:
Производительность источника рассчитывается по формуле,
![]()
где T – время, затрачиваемое в среднем на каждое сообщение при передаче, и определяемое в соответствии со следующим выражением:
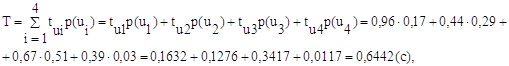
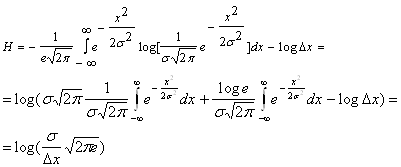
а энтропия источника H(U) в соответствии с формулой (1.4) [1] равна:
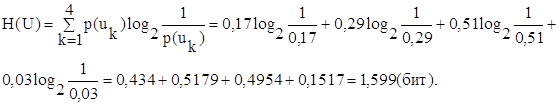
Итак, производительность источника равна:

2. Расчёт информационных характеристик дискретного канала
2.1 Задача № 2.23
На вход дискретного симметричного канала, показанного на рисунке 2, без памяти поступают двоичные символы ![]() и
и ![]() с априорными вероятностями p(U1)=0,75 и p(U2)=0,25.
с априорными вероятностями p(U1)=0,75 и p(U2)=0,25.
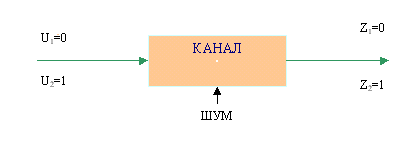
Рисунок 2 – Дискретный симметричный канал
Переходные вероятности ![]() в таком канале задаются соотношением
в таком канале задаются соотношением
![]() ,
,
где p=0,1 – вероятность ошибки. Определить все апостериорные вероятности ![]() .
.
Решение:
![]() - переходные вероятности того, что на выходе будет символ zjпри условии, что на входе был символ ui.
- переходные вероятности того, что на выходе будет символ zjпри условии, что на входе был символ ui.
![]() - апостериорные вероятности того, что на входе канала имел место символ ui при условии, что на выходе наблюдается zj.
- апостериорные вероятности того, что на входе канала имел место символ ui при условии, что на выходе наблюдается zj.
По формуле Байеса:

Итак, 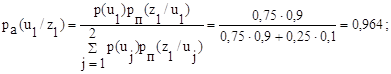
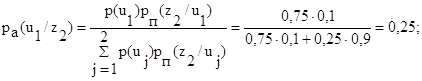

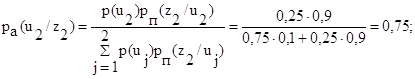
2.2 Задача № 2.48
Двоичный источник с равновероятными элементами имеет производительность U’=1500 бит в секунду. При передачи по каналу в среднем один из 100 символов принимается ошибочно. Определить скорость передачи инфориации по данному каналу.
Решение:
U1 Z1 “1”
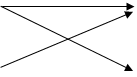
U2 Z2 “0”
Рисунок 3 – Дискретный канал
Ситуация в канале характеризуется данным рисунком 3. В среднем один из 100 символов принимается ошибочно, поэтому вероятность ошибки будет составлять ро=1/100=0,01. Тогда вероятность правильного принятия будет вычисляться из следующего выражения: 1-р0=1-0,01=0,99.
Таким образом, канал описывается распределением вероятностей:
P(Z1/U1)=P(Z2/U2)=0,99
P(Z1/U2)=P(Z1/U2)=0,01
P(U1)=P(U2)=0,5- дано по условию
Скорость передачи информации вычисляется по формуле:
I’(U,Z)=H’(U)-H’(U/Z),
а энтропия будет равна 1 биту, так как
0,5log2+0,5log2=1
H’(U)=VC*H(U), где VC=1500 c-1
I’(U,Z)=H’(U)-H’(U/Z)
H’(U/Z)=VC*H(U/Z)
![]()
Условные вероятности можно найти по формуле Байеса:

H(U/Z)=-P(Z1)[P(U1/Z1)log2P(U1/Z1)+P(U2/Z1)log2P(U2/Z1)]-P(Z2)[P(U1/Z2)log2P(U1/Z2)+ P(U2/Z2)log2P(U2/Z2)]
H(U/Z)=-(0.5+0.5)(-2*0.99log(0.99)-2*0.01*log(0.01))=0.16
H’(U/Z)=VC*H(U/Z)=1500*0,16=241 (бит)
I’(U,Z)=H’(U)-H(U/Z)=1500-241=1259(бит/с)
Похожие работы
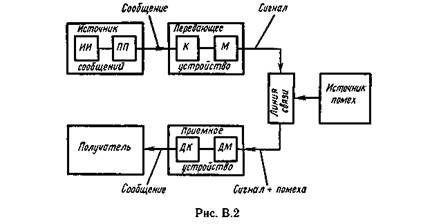
... дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, т.е. в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с импульсно–кодовой модуляцией (ИКМ) и дельта–модуляцией (ДМ). Для преобразования непрерывного сообщения в цифровую ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...

0 комментариев