Навигация
Согласование дискретного источника с дискретным каналом
3. Согласование дискретного источника с дискретным каналом
3.1 Задача № 3.23
Закодировать двоичным кодом Фано ансамбль сообщений {ai}:
{0.08, 0.001, 0.06, 0.09, 0.017, 0.18, 0.4, 0.06, 0.003, 0.027, 0.014, 0.068}
Закодировать произвольную комбинацию, состоящую из 5 символов из ансамбля{ai}. Определить потенциальный минимум среднего количества символов кода, приходящихся на одно сообщение ансамбля {ai} и среднее количество символов, разработанного кода Фано, приходящихся на одно сообщение из ансамбля {ai}. Рассчитать эффективность разработанного кода.
Решение.
Кодируется кодом Фано заданный ансамбль сообщений следующим образом.
Таблица 1 - Кодирование ансамбля сообщений {ai} двоичным кодом Фано
| сообщение | вероятность | код |
| а7 | 0,4 | 00 |
| а6 | 0,18 | 01 |
| а4 | 0,09 | 100 |
| a1 | 0,08 | 1010 |
| а12 | 0,068 | 1011 |
| а3 | 0,06 | 1100 |
| а8 | 0,06 | 1101 |
| а10 | 0,027 | 1110 |
| а5 | 0,017 | 11110 |
| а11 | 0,014 | 111110 |
| а9 | 0,003 | 1111110 |
| a2 | 0,001 | 1111111 |
Сообщения источника располагаются в порядке не возрастания их вероятностей, делятся на две части так, чтобы суммарные вероятности сообщений в каждой части были по возможности равны. Сообщениям первой части приписывается в качестве первого символа нуль, а сообщениям второй части единица. Затем каждая из этих частей (если она содержит более одного сообщения) опять делится на две примерно равные части и в качестве второго символа для первой из них берется 0, а для второй 1. Этот процесс повторяется до тех пор, пока в каждой из полученных частей не останется по одному сообщению.
После использования полученных комбинаций символов, закодируется произвольная комбинация, состоящая из 5 символов из ансамбля {ai}: 101011111110010011110.
Среднее количество символов, приходящихся на одно сообщение, определяется по формуле 2.9 курса лекций:
![]() ,
,
где ms – количество позиций, а ps – вероятность сообщения из ансамбля {ai}.
![]()
Определяется минимальное среднее количество символов, приходящихся на одно сообщение, по формуле
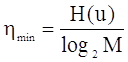 ,
,
где M – объем алфавита кода, равный 2, а H(U) энтропия источника.
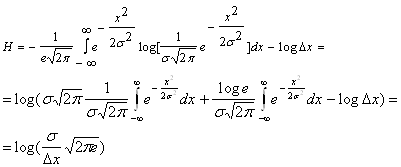
Далее находится энтропия:
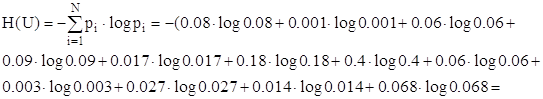
![]()
![]()
![]()
![]()
![]()
Затем вычисляется величина ψ-эффективность кода, которая характеризует степень близости неравномерного статистического кода к оптимальному.
![]()
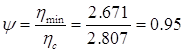
3.2 Задача № 3.56
Определить избыточность оптимального по Шеннону кода (существование которого утверждается теоремой для канала с шумом) с объемом алфавита m и средним количеством символов, переданных в единицу времени Vk, предназначенного для безошибочной передачи информации по каналу с пропускной способностью С.
Найти минимально возможную избыточность оптимального кода для симметричного канала при m = 8 и вероятности ошибки P = 0,08.
Решение:
Избыточность кода вычисляется по следующей формуле:
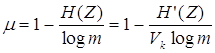 ,
,
где H¢(Z)=Vk*H(Z)
Так как передача информации предполагается безошибочной, то кодирование должно быть однозначным, то есть потери информации при кодировании должны отсутствовать. Это означает, что:
H¢(Z)=H¢(U),
где H¢(U)- производительность источника, который передает информацию.
В соответствии с условием теоремы Шеннона
H¢(U) < C, а H(U) = С + ε = С; (ε→0),
тогда формула избыточности будет выглядеть следующим образом:
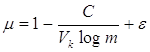 , при ε→0
, при ε→0
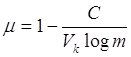
Для двоичного симметричного канала справедливо выражение:
C=Vk*[1+p*log2p+(1-p)*log2(1-p)]
Подставив известные значения в формулы, получается:
C=Vk*0.6
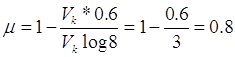
Похожие работы
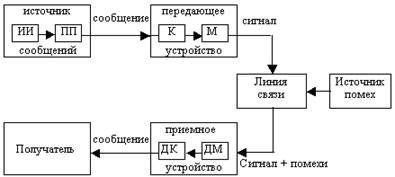
... дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, т.е. в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с импульсно–кодовой модуляцией (ИКМ) и дельта–модуляцией (ДМ). Для преобразования непрерывного сообщения в цифровую ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...

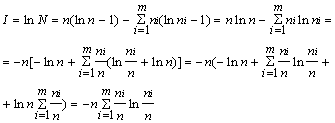
0 комментариев