Навигация
Дискретизация и квантование
4. Дискретизация и квантование
4.1 Задача № 4.23
|
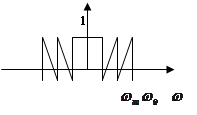
![]()
![]() Рисунок 4 - Непрерывный сигнал x(t), имеющий спектр X(jω) дискретизируется с частотой дискретизации ωд
Рисунок 4 - Непрерывный сигнал x(t), имеющий спектр X(jω) дискретизируется с частотой дискретизации ωд
Выполняется ли в данном случае условие теоремы Котельникова? Построить график спектра дискретизированного сигнала (изобразить 5 периодов спектра). Проиллюстрировать графически процесс восстановления спектра непрерывного сигнала с помощью идеального интерполирующего фильтра по спектру дискретного сигнала.
Решение:
При построении графика спектра дискретизированного сигнала (рисунок 4) исспользуется выражение (3.16) [1], причём для изображения 5 периодов спектра следует учесть 5 слагаемых:
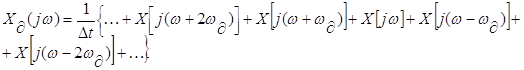
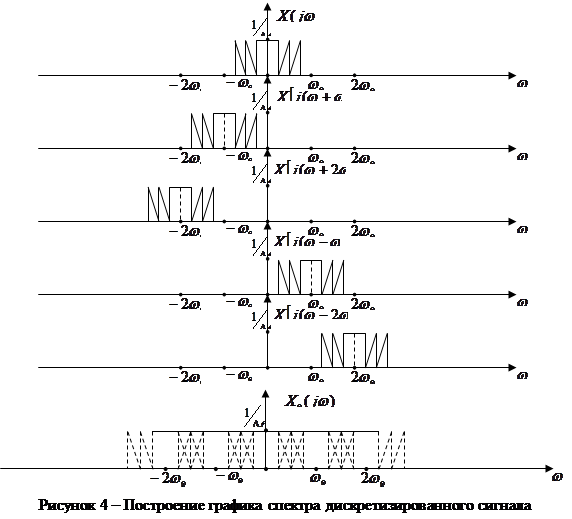
Процесс восстановления спектра непрерывного сигнала с помощью идеального интерполирующего фильтра по спектру дискретного сигнала проиллюстрирован графически на рисунке 5, где первый график представляет собой частотную характеристику идеального фильтра низких частот, а ![]() - спектр сигнала на выходе интерполятора.
- спектр сигнала на выходе интерполятора.
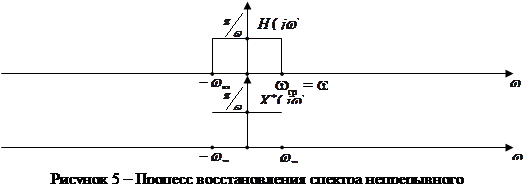
Условие теоремы Котельникова (неравенство (3.17) [1]) в данном случае не выполняется (т.к. ![]() ), из-за взаимного перекрытия слагаемых
), из-за взаимного перекрытия слагаемых ![]() происходит изменение формы спектра
происходит изменение формы спектра ![]() и точное восстановление
и точное восстановление ![]() , а следовательно и x(t), невозможно.
, а следовательно и x(t), невозможно.
4.2 Задача № 4.52
Непрерывный сигнал ![]() дискретизируется с частотой дискретизации ωд=2,5. Построить графики непрерывного и дискретизированного сигналов (изобразить не менее пяти периодов). Проиллюстрировать графически процесс восстановления непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка.
дискретизируется с частотой дискретизации ωд=2,5. Построить графики непрерывного и дискретизированного сигналов (изобразить не менее пяти периодов). Проиллюстрировать графически процесс восстановления непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка.
Решение:
Зная выражение, описывающее непрерывный сигнал, и частоту дискретизации, найдём период дискретизации ![]() , необходимый при построении графика дискретизированного сигнала, выразив его через период Т непрерывного сигнала:
, необходимый при построении графика дискретизированного сигнала, выразив его через период Т непрерывного сигнала:
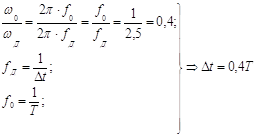 .
.
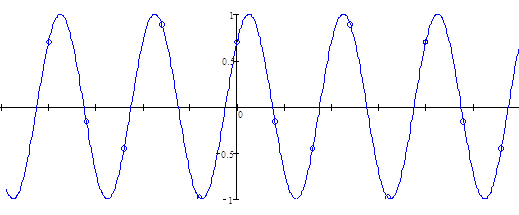
Графики исходного непрерывного и дискретизированного сигналов представлены на рисунке 6.
|
|
|

Интерполятором называется фильтр, преобразующий отсчёты дискретного сигнала в непрерывный сигнал. Процесс восстановления сводится к подаче дискретного сигнала на вход фильтра, с выхода которого снимается непрерывный сигнал. Математически процесс восстановления сигнала описывается следующим выражением:
![]() ,
,
где ![]() - сигнал на выходе интерполятора;
- сигнал на выходе интерполятора;
![]() - отсчёты дискретного сигнала;
- отсчёты дискретного сигнала;
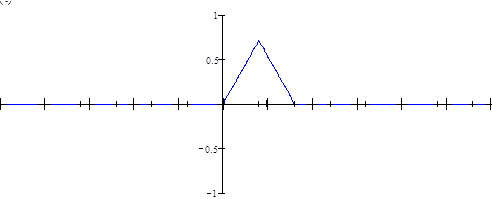
![]() - импульсная характеристика фильтра, для интерполятора 1-ого порядка она имеет вид, представленный на рисунке 7.
- импульсная характеристика фильтра, для интерполятора 1-ого порядка она имеет вид, представленный на рисунке 7.
|
|

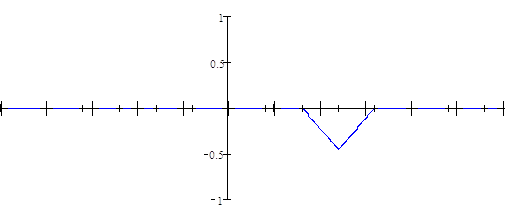
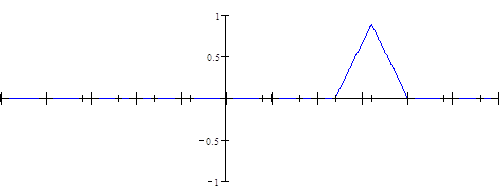
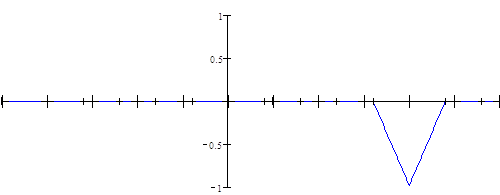
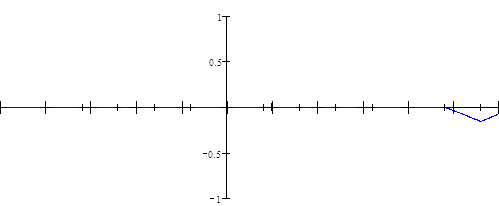
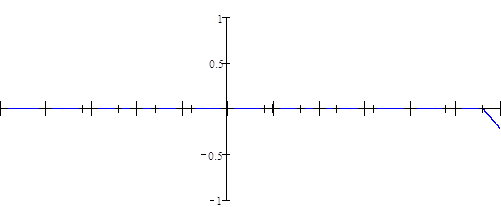
Итак, процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка проиллюстрирован графически на рисунке 8, где последний график описывает сигнал, получившийся на выходе интерполятора.
|
|
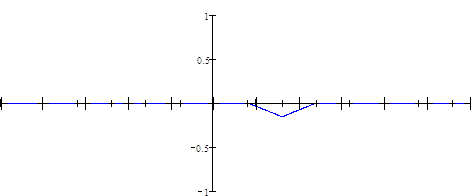
Рисунок 8 Лист 21 - Процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка
![]()
|
![]()
|
|
![]()
|

Рисунок 8 Лист 22 - Процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка
![]()
|
![]()
|
![]()
|

|
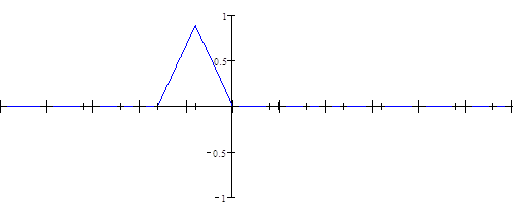
Рисунок 8 Лист 23 - Процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка
|
|

![]()
|
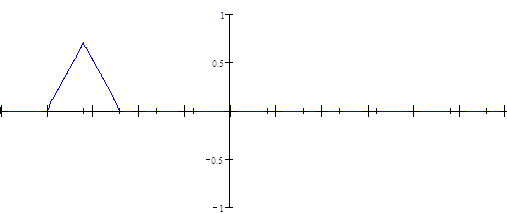
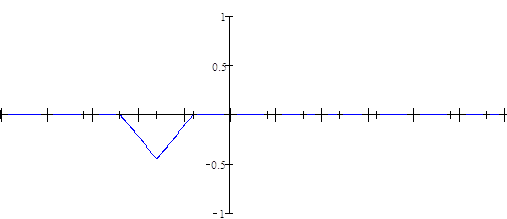
Рисунок 8 Лист 24 - Процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка
|
|
|

Рисунок 8 Лист 25 - Процесс восстановления заданного непрерывного сигнала по дискретному во временной области с помощью интерполятора 1-го порядка
4.3 Задача № 4.67
Непрерывное сообщение u(t) квантуется с округлением с постоянным шагом Du при числе уровней квантования Ny=45. Плотность распределения вероятностей сообщения Wu(U) равномерна в интервале от –Um до Um, т.е.
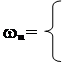
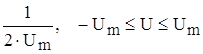
0, при др. U
Определить соотношение сигнал – шум в квантованном сообщении.![]()
Решение:
Соотношение сигнал – шум определяется как отношение мощности сигнала к мощности шума, т.е.
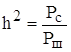 ,
,
где Рс и Рш находятся как дисперсия случайной величины Uc и Uш, следовательно,
![]()
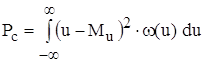 ,
,
где Mu – математическое ожидание, которое определяется как:
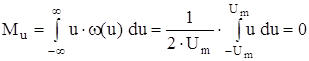 .
.
Исходя из значения математического ожидания, получается:
![]()
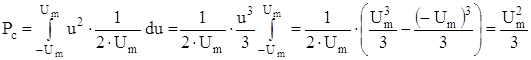 .
.
Согласно условию задачи квантование производится с округлением, следовательно, дисперсия или мощность шума определяется формулой
![]() .
.
Подставляя полученные значения в выражение для нахождения соотношения сигнал – шум, получается:

В соответствии с формулой 3.1 а курса лекций
![]() , откуда:
, откуда:
 .
.
Известно, что Ny=45, получается
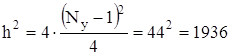
Заключение
В результате выполнения работы изучен необходимый теоретический материал, решены все задачи в соответствии с вариантом задания, получены навыки расчёта информационных характеристик источников дискретных сообщений и дискретного канала, изучены процессы согласования дискретного источника с дискретным каналом, дискретизации и квантования, т.о. задание курсового проекта выполнено в полном объёме.
Похожие работы
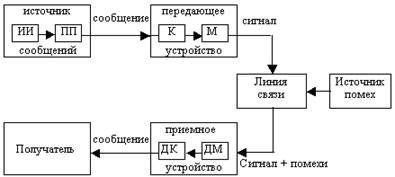
... дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, т.е. в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с импульсно–кодовой модуляцией (ИКМ) и дельта–модуляцией (ДМ). Для преобразования непрерывного сообщения в цифровую ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...

0 комментариев