Конечные разности и аппроксимация производных

1.3 Конечные разности и аппроксимация производных

1.3.1 Определение конечных разностей

Конечная разность "вперед" для таблично заданной функции в i-той точке определяется выражением: , где функция  задана, как функция целочисленного аргумента с единичным шагом по аргументу i.

Для аналитически заданной и протабулированной с постоянным шагом h функции f(x) определяющее соотношение имеет вид:

f(x) = f(x+h) - f(x)

Преобразование таблицы функции f(x) в функцию целочисленного аргумента g(i) осуществляют при помощи линейного соотношения между аргументами x и i :  .

Повторные конечные разности n-го порядка в i-той точке для табличной функции g(i) определяются соотношением

Линейность конечно-разностного оператора  позволяет ввести конечно-разностный оператор сдвига E=(1+) и многочлены от оператора  с целыми коэффициентами, такие, как

и т.п.,

где 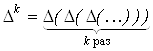должно рассматриваться в качестве оператора повторной разности k-го порядка .

Применение оператора сдвига к g(i) преобразует последнее в g(i+1) :

g(i+1) = Eg(i) = (1+)g(i)= g(i) + g(i).

Повторное применение оператора сдвига позволяет выразить значение ординаты функции g(i) в точке (i+n) через конечные разности различных порядков:

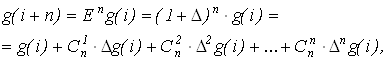
где - число сочетаний из n элементов по k ;

-

многочлен степени k от целой переменной n (), имеющий k сомножителей. При k=n  .

Относительно начала координат (i=0 - начало таблицы) функция целочисленной переменной g(n) представляется разложением по многочленам различных степеней от 0 до n. Для больших степеней конечные разности равны нулю.

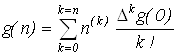
С другой стороны, так как  , то

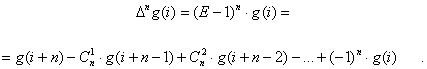
Таким образом, любая повторная конечная разность выражается взвешенной алгебраической суммой ординат табличной функции.

1.3.2 Взаимосвязь операторов разности и дифференцирования

Значение функции на удалении h от некоторой точки  можно выразить через значения производных в этой точке, разложив ее в ряд Тэйлора:

где - оператор дифференцирования,

 - оператор сдвига, выраженный через оператор p .

h- шаг по оси действительной переменной

Из равенства операторов сдвига, выраженных через p и , можно получить взаимосвязь этих линейных операторов:

,

Оператор дифференцирования порядка n, перенесенный в точку, например, на 2 шага вперед представляется так:

Если алгебраически перемножить многочлены с конечно-разностными операторами и ограничиться операторами со степенью не выше n, то получится одна из возможных аппроксимаций оператора дифференцирования. Например, для n=2 и четырех точечном задании функции f(x), отбросив повторные разности выше третьего порядка, получим:

.

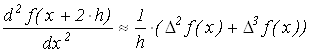Выразив повторные разности через ординаты табличной функции, получим второй вариант аппроксимации оператора дифференцирования:

 .

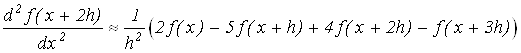Для целочисленного аргумента табличной функции запись выражения можно упростить, так как шаг h=1 и :

 .

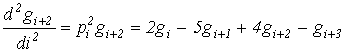Для k-той производной в точке m от начала интервала [0,n]:

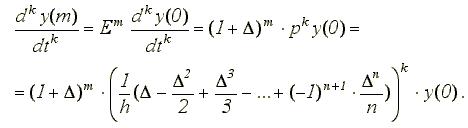
После выполнения операций возведения многочленов в степень и их перемножения, конечные разности со степенями больше n отбрасываются, а оставшиеся  заменяются выражением . Раскрыв скобки, подставив  и сгруппировав подобные члены, получим аппроксимирующую сумму из (n+1)-й ординаты функции:

 .

Коэффициенты  минимальны для точек середины интервала (m=n/2) и максимальны - для крайних. Аналогично ведут себя и коэффициенты в выражении погрешности аппроксимации.

Таким образом, для любой внутренней точки из группы выбранных равномерно расположенных ординат можно сформировать выражение, аппроксимирующее производную взвешенной суммой.