Навигация
Представление уравнений конечно-разностной моделью
1.4 Представление уравнений конечно-разностной моделью
При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями.
Для аппроксимации таких уравнений удобно заранее построить таблицы коэффициентов для выражений производных по заданному числу значений функции. В бакалаврской работе воспользуемся аппроксимацией по трем и пяти точкам, коэффициенты для которых приведены в таблицах 1, 2, 3, 4. В крайних справа колонках таблиц приведены коэффициенты выражений, вынесенных в заголовок колонки, для погрешности аппроксимации производной в выбранной точке. В выражениях погрешности присутствуют значения производных функции с порядками выше порядка аппроксимируемой производной.
Таблица 1 - Аппроксимация первой производной по трем точкам
|
| y(0) | y(1) | y(2) |
|
| y’(0) | -3 | 4 | -1 | 2 |
| y’(1) | -1 | 0 | 1 | -1 |
| y’(2) | 1 | -4 | 3 | 2 |
Таблица 2 - Аппроксимация второй производной по трем точкам
|
|
|
|
|
|
|
| 1 | -2 | 1 | -12, 2 |
|
| 1 | -2 | 1 | 0, -1 |
|
| 1 | -2 | 1 | 12, -2 |
Таблица 3 - Аппроксимация первой производной по пяти точкам
|
|
|
|
|
|
|
|
|
| -25 | 48 | -36 | 16 | -3 | 12 |
|
| -3 | -10 | 18 | -6 | 1 | -3 |
|
| 1 | -8 | 0 | 8 | -1 | 2 |
|
| -1 | 6 | -18 | 10 | 3 | -3 |
|
| 3 | -16 | 36 | -48 | 25 | 12 |
Таблица 4 - Аппроксимация второй производной по пяти точкам
|
|
|
|
|
|
|
|
|
| 35 | -104 | 114 | -56 | 11 | -150, 12 |
|
| 11 | -20 | 6 | 4 | -1 | 15, -3 |
|
| -1 | 16 | -30 | 16 | -1 | 0, 2 |
|
| -1 | 4 | 6 | -20 | 11 | 15, 3 |
|
| 11 | -56 | 114 | -104 | 35 | 150, -12 |
Чтобы получить конечно-разностную модель дифференциального уравнения, необходимо сначала интервал или область решения разделить с постоянным шагом по осям координат на требуемое число подинтервалов и для каждой внутренней точки подставить аппроксимирующие выражения в заданное уравнение. После приведения подобных членов в каждом уравнении, получится система алгебраических уравнений при полной дискретизации всех независимых переменных или система дифференциальных уравнений - при неполной дискретизации. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области.
В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Поэтому аппроксимирующие, выражения производных из таблиц 1-4 для точек у левой границы интервала берутся из верхних строчек, а для точек у правой границы - из нижних строчек.
Похожие работы
... равенства и неравенства. При полном равенстве в распределении доходов "кривая Лоренца" представляла бы собой прямую и, наоборот, кривизна усиливается по мере роста неравенства. В соответствии с современной экономической теорией нежелательно как абсолютное равенство в распределении доходов, так и резкий разрыв в уровне жизни различных групп населения. Абсолютное равенство в доходах не стимулирует ...
... . Сложность совместной работы и обмена имеющейся информацией обусловлена ее высокой стоимостью, секретностью, проблемами достоверности и совместимости данных. 2.3 Информационные технологии управления муниципальной недвижимостью Эффективное управление объектами недвижимости должно обеспечить: - полный учет объектов муниципальной собственности; - эффективный контроль за использованием ...
... интервал времени. В этом случае поведение АСОД может быть представлено только в дискретных точках (группа динамических моделей с дискретным временем). 6 Описание программы автоматизации учета исполнения бюджета Краснодарского края 6.1 Средства разработки 6.1.1 Компилятор BORLAND PASCAL 7.0 Программа написана на языке Turbo Pascal версии 7.0. Турбо Паскаль появился на рынке программных ...

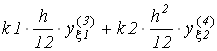


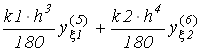
0 комментариев