Навигация
Математическая постановка транспортной задачи
62893
знака
11
таблиц
17
изображений
2.1 Математическая постановка транспортной задачи
В общем случае математическая постановка транспортной задачи может быть сформулирована в следующем виде. Имеется m пунктов производства или хранения и n пунктов потребления некоторого однородного продукта (например, уголь, песок цемент и т. п.). Для каждого из пунктов задан аi –объем производства или запаса продукта в i-том пункте (i
{1,2,…,m}), а для каждого пункта потребления задана bj – потребность в продукте в j-том пункте потребления (j{1,2,…,n}). Известна сij – стоимость перевозки или транспортировки одной единиц продукта из i-го пункта производства в j-й пункт потребления. Требуется определить оптимальный план перевозок продукта, так чтобы потребность во всех пунктах потребления были удовлетворены, а суммарные затраты на транспортировки всей продукции были минимальными.
Ведем в рассмотрение следующие переменные: хij- количество транспортируемого продукта или объем перевозок из i-го пункта производства в j-й пункт потребления. Тогда в общем случае математическая постановка транспортной задачи может быть сформулирована следующим образом.
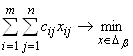, (2.1)
где множество допустимых альтернатив 
формируется следующей системой отграничений типа неравенств:
Следует заметить, что, в отличие от стандартной задачи линейного программирования, в математической постановке транспортной задачи в виде (2.1)-(2.2) для удобства используются переменные с двумя индексами.
При этом общее число переменных транспортной задачи равно: m
n, что делает возможным сформулировать эквивалентную математическую постановку транспортной задачи с одноиндексными переменными.
Классическая транспортная задача линейного программирования является сбалансированной или закрытой, т.е. формулируется в форме, когда имеет место равенство общего объема производства рассматриваемого продукта общему объему его потребления. Этому условию соответствует отдельное ограничение (2.5). В противном случае, если равенство (2.5) не имеет места, то транспортная задача называется несбалансированной или открытой.
На практике встречаются различные модификации транспортной задачи. Наиболее известные из них используют дополнительную структуру типа графа для задания структуры транспортной сети, соединяющей пункты производства и потребления. Соответствующая транспортная задача может быть сформулирована в сетевой постановке применительно к конкретному графу и поэтому относится к классу задач оптимизации на графах.
В то же время классическая транспортная задача может быть дополнена условиями на ограничение сверху возможных значений некоторых или всех переменных: 
где hij-пропускная способность транспорта между i-м пунктом производства и j-м пунктом потребления. Как нетрудно заметить, подобная модификация приведет к включению в модель (2.1)-(2.5) дополнительных ограничений. Однако эти дополнительные ограничения не оказывают существенного влияния на процесс их решения с помощью программы Ms Excel.
2.2 Решения транспортной задачи с помощью программы Ms Excel
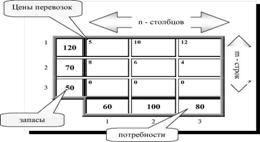
Для решения классической транспортной задачи с помощью программы Ms Excel необходимо задать конкретные значения параметрам исходной задачи. Для определения рассмотрим задачу оптимального планирования перевозок бензина некоторой марки между нефтеперерабатывающими заводами (НПЗ) и автозаправочными станциями (АЗС). В этом случае в качестве транспортируемого продукта рассматривается бензин, в качестве пунктов производства- 3 нефтеперерабатывавающих завода (т=3), а в качестве пунктов потребления- 4 автозаправочные станции (п=4).
Объемы производства бензина следующие: НПЗ №1- 10 т, НПЗ №2- 14 т, НПЗ №3- 17 т. Объемы потребления бензина следующие: АЗС №1-15 п, АЗС №2- 12 п, АЗС №3-8,5 т, АЗС №4-5,5 т. Стоимость транспортировки одной тонны бензина между НПЗ и АЗС заданна в форме следующей таблицы:
Таблица 2.1. Стоимость транспортировки бензина
Между НПЗ и АЗС (в тысяч тенге)
| Пункты потребления / Пункты производства | АЗС №1 | АЗС №2 | АЗС №3 | АЗС №4 |
| НПЗ №1 | 3 | 5 | 7 | 11 |
| НПЗ №2 | 1 | 4 | 6 | 3 |
| НПЗ №3 | 5 | 8 | 12 | 7 |
Соответствующая математическая постановка рассматриваемой индивидуальной транспортной задачи может быть записана в следующем виде:
3х11+5х12+7х13+11х14+х21+4х22+6х23+3х24+ (2.6)
+5х31+8х32+12х33+7х34→
где множество допустимых альтернатив
формируется следующей системой ограничений типа равенств:
(2.7)
Заметим, что первые 3 ограничения данной задачи соответствуют общему ограничению (2.2), следующие 4 ограничения- общему ограничению (2.3), а последнее ограничение- общему ограничению (2.5).
При этом общее ограничение (2.4), соответствующее требованию сбалансированности транспортной задачи не входит в математическую модель рассматриваемой индивидуальной задачи. Это вполне допустимо, поскольку непосредственная проверка позволяет установить выполнение общего ограничения (2.4), а значит, исходная транспортная задача (2.6) и (2.7) является сбалансированной.
Для решения сформулированной индивидуальной транспортной задачи с помощью программы MS Excel создадим в книге Линейное программирование новый лист и изменим его имя на Транспортная задача. Для решения задачи выполним следующие подготовительные действия:
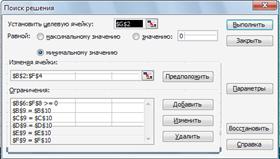
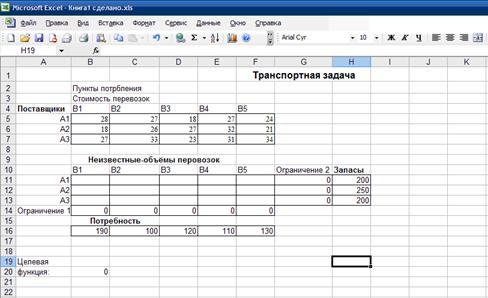
1.Внесем необходимые надписи в ячейки A5:A10, B1, F1. B5:G5, как это изображено на рисунке 2.1. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решения рассматриваемой транспортной задачи.
2. В ячейки В2:Е4 введем значение коэффициентов целевой функции (таблица 2.1).
3. В ячейки F2, введем формулу: =суммпроизв(В2:Е2; В6:Е8), которая представляет целевую функцию (2.6).
4. В ячейки G6:G8 и B10:E10 введем значения, соответствующие правым частям ограничений (2.7).
5. В ячейку F6 введем формулу: =сумм (В6:Е6), которая представляет первое ограничение (2.7).
6. Скопируем формулу, введенную в ячейку F6, в ячейки F7 и F8.
7. В ячейку В9 введем формулу: =сумм (В6:В8), которая представляет четвертое ограничение (2.7).
8. Скопируем формулу, введенную в ячейку В9, в ячейки C9, D9 и E9.
Внешний вид рабочего листа MS Office Excel с исходными данными для решения транспортной задачи показан на рисунке 2.1.
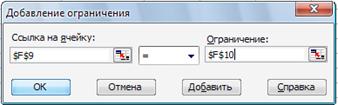
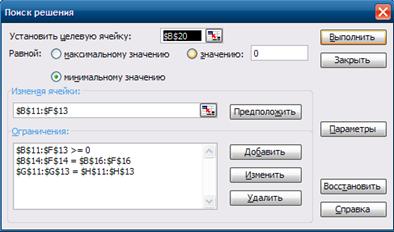
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис│Поиск решения…
После появления диалогового окна Поиск решения следует выполнить следующие действия:
1.В поле с именем Установить целевую ячейку: ввести абсолютный
адрес ячейки $F$2.
2.Для группы Равной: выбрать вариант поиска решения- минимальному значению.
Рисунок. 2.1 Исходные данные для решения
транспортной задач
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
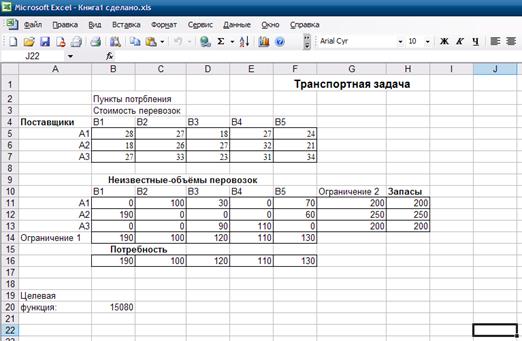
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...
... ). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. · В ячейки E5:I5 - заявки на продукцию, ...
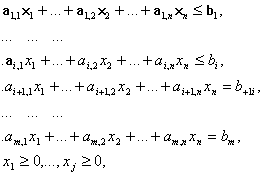
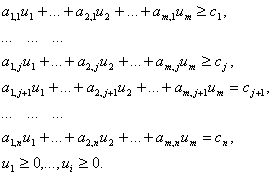
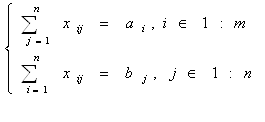
0 комментариев