Навигация
В поле с именем Изменяя ячейки: ввести абсолютный адрес диапазона ячеек $B$2:$E$4
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес диапазона ячеек $B$2:$E$4.
4.Добавить 7 ограничений, соответствующих базовым ограничениям исходной постановки решаемой транспортной задачи. С этой целью выполнить следующие действия:
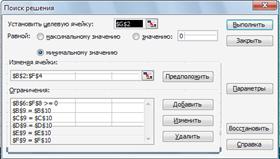
· для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
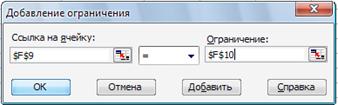
· в появившемся дополнительном окне выбрать ячейку $F$6, которая
должна отобразиться в поле с именем Ссылка на ячейку;
· в качестве знака ограничений из выпадающего списка выбрать строгое неравенство “=”;
· в качестве значения правой части ограничения выбрать ячейку $С$6;
· для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
· аналогичным образом задать оставшиеся 6 ограничений.
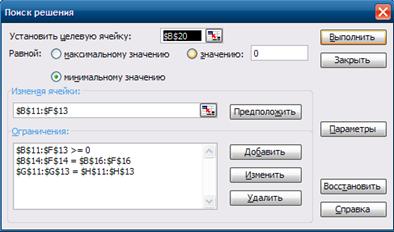
5.Добавить последнее ограничение на неотрицательность значений переменных задачи. Внешний вид диалогового окна мастера поиска решения с ограничениями для транспортной задачи изображен на рисунке 2.2.
6.В дополнительном окне параметров поиска решения следует выбрать отметки Линейная модель и Неотрицательные значения.
Рисунок 2.2. Параметры мастера поиска решения и базовых
 ограничения для транспортной задачи
ограничения для транспортной задачи
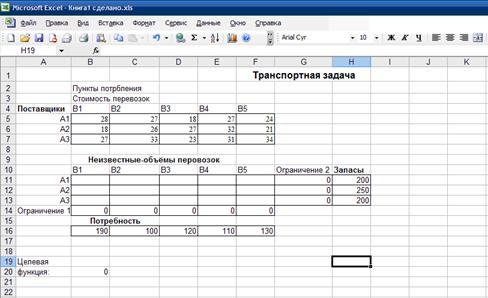
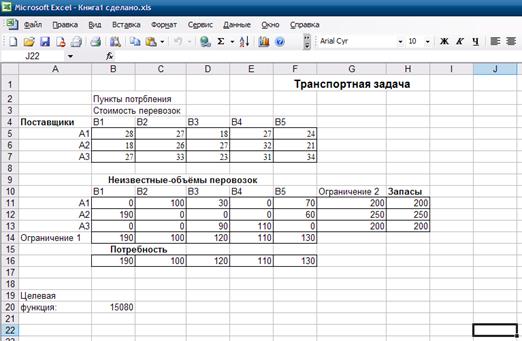
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид рисунок 2.3.
Рисунок 2.3 Результат количественного
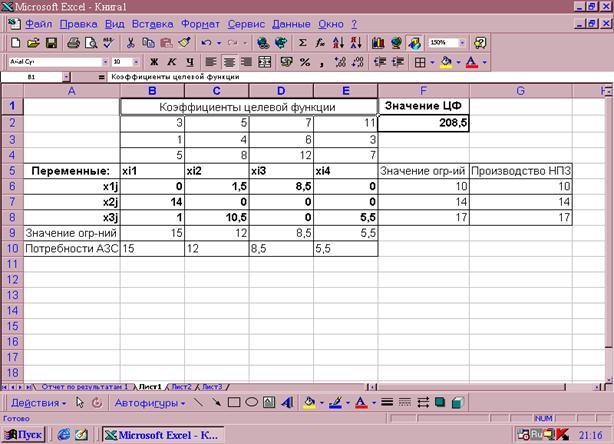 решения транспортной задачи
решения транспортной задачи
Результатом решения транспортной задачи являются найденные оптимальные значения переменных: х11=0, х12=1,5, х13=8,5, х14=0, х21=14, х22=0, х23=0, х24=0, х31=1, х32=10,5, х33=0, х34=5,5, которым соответствует значение целевой функции: f opt = 208,5. При выполнении расчетов для ячеек В6:Е8 был выбран числовой формат с тремя знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения потребностей АЗС №1 следует транспортировать 14т бензина из НПЗ №2 и 1т- из НПЗ №3, для удовлетворения потребностей АЗС №2 следует транспортировать 1,5 т бензина из НПЗ №1 и 10,5т – из НПЗ №3, для удовлетворения потребностей АЗС №3 следует транспортировать 8,5 т бензина из НПЗ №1 и, наконец, для удовлетворения потребностей АЗС №4 следует транспортировать 5,5 т бензина из НПЗ №3. При этом общая стоимость найденного плана перевозок составит 208,5 тысяч тенге.
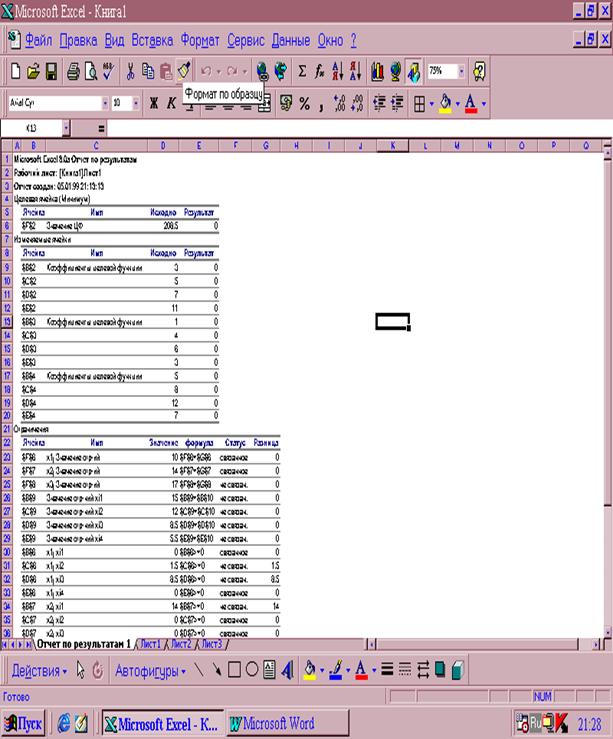 Рисунок 2.4 Отчет по результатам поиска решения
Рисунок 2.4 Отчет по результатам поиска решения
2.3 Решение транспортной задачи с помощью методов
потенциалов
Для оценки точности и правильности результатов решения транспортных задач линейного программирования, полученных с помощью программных средств, в общем случае можно воспользоваться симплекс-методом. Однако специально для решения транспортной задачи линейного программирования был разработан метод потенциалов. Основная идея этого метода основывается на критерии оптимальности, который может быть сформулирован следующим образом.
Для того чтобы исходная закрытая транспортная задача линейного программирования (2.1) - (2.5) имела оптимальное решение, необходимо и достаточно существование таких неотрицательных чисел {v1,v2,v3,…,vn, u1,u2,…,um}, которые обеспечивают выполнение двух групп условий:
![]() , (2.8)
, (2.8)
и если некоторое
![]() >0 то ui+uj=cij. (2.9)
>0 то ui+uj=cij. (2.9)
Соответствующие данным условиям числа {v1,v2,…,vn, u1,u2,…,um} получили название потенциалов. Очевидно, данные условия могут служить признаком окончания поиска решения транспортной задачи.
Общая идея определения оптимального решения транспортной задачи методом потенциалов аналогична идее решения задачи линейного программирования симплекс-методом, а именно: сначала находят некоторое начальное допустимое решение транспортной задачи, а затем его последовательно улучшают до получения оптимального решения. В общем случае алгоритм метода потенциалов имеет итеративный характер и заключается в выполнении следующих действий:
1. Если исходная транспортная задача линейного программирования является открытой, то она преобразуется к замкнутому виду (2.1)- (2.5). С этой целью могут быть введены дополнительные переменные {xm+1,j}![]() для фиктивного пункта производства am+1, если выполняется неравенство:
для фиктивного пункта производства am+1, если выполняется неравенство: ![]() или дополнительные переменные
или дополнительные переменные ![]() для фиктивного пункта потребления bn+1, если выполняется неравенство:
для фиктивного пункта потребления bn+1, если выполняется неравенство: ![]()
При этом дополнительным переменным должны соответствовать нулевые коэффициенты целевой функции: cm+1,1=cm+1,2=…=cm+1,n=0 или c1,n+1=c2,n+1=…=cm,n+1=0. Тем самым, с точностью до обозначений индексов переменных, в качестве исходной транспортной задачи будем рассматривать ее математическую модель в замкнутой форме (2.1)- (2.5).
2. Для транспортной задачи в замкнутой форме (2.1)-(2.5) находится некоторое начальное допустимое решение, которое записывается в специальную таблицу следующего вида таблица 2.2.
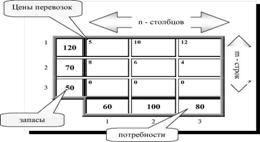
Рассмотрим особенности построение данной таблицы. Верхняя строка и левый столбец содержат искомые значения потенциалов, которые требуется отыскать на последующих этапах алгоритма, и значения правых частей ограничений (2.2)-(2.3).
Таблица 2.2. Общий вид таблицы метода потенциалов
| F(x) | v1 b1 | v2 b2 | …. | vn bn |
| u1 a1 | c11 x11 | c12 x12 | … | c1n x1n |
| u2 a2 | c12 x12 | c22 x22 | c2n x2n | |
| … | … | … | … | … |
| um am | cm1 xm1 | cm2 xm2 | … | cmn xmn |
В каждой ячейке таблицы содержится два значения: cij- стоимость транспортировки единицы продукта из i–го пункта производства в j–й пункт потребления и xij - значения переменных начального допустимого решения. При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ячейка называется занятой. Самая верхняя слева ячейка исходной таблицы содержит значение целевой функции (1) для содержащегося в таблице промежуточного решения. При этом значение целевой функции рассчитывается по формуле: F(x)=c11x11+c12x12+…+cnmxnm, где хij-ненулевые элементы таблицы 2.2, соответствующие переменным решаемой задачи.
Следует заметить, что первые два этапа метода потенциалов является подготовительными. Все последующие действия имеют итеративный повторяющийся характер и выполняются в рамках построенной исходной таблицы.
3. Для построенной таблицы 2 находятся значения потенциалов пунктов производства и потребления: v1, v2,… vn, u1,u2,…um. С этой целью составляется и решается следующая система линейных уравнений:
![]() (2.10)
(2.10)
где индексы i и j соответствуют только ненулевым значениям переменных xij или занятым ячейкам таблицы 2.2. Как не трудно заметить, существование решения системы уравнений (2.10) обеспечивает выполнение второй группы условий критерия оптимальности (2.9). Для удобства найденные значения записываются в таблицу 2.2.
4. Для найденного решения системы уравнений (2.1) проверяется первая группа условий (2.8) критерия оптимальности. С этой целью вначале рассчитываются оценки свободных ячеек таблицы 2 по следующей формуле:
![]() (2.11)
(2.11)
где индексы i и j соответствуют только нулевым значениям переменных xij или занятым ячейкам таблицы 2.2. В этом случае проверка первой группы условий критерия оптимальности найденного решения сводится к проверке следующего условия только для ячеек:
![]() (2.12)
(2.12)
Если условие (2.12) выполняется, то найденное решения является оптимальным, и на этом дальнейшие расчеты могут быть завершены. Если же условие (2.12) не выполняется, то следует перейти к выполнению следующего этапа алгоритма метода потенциалов.
Из всех ![]() выбирается наименьшее значение (если их несколько- то любое из них). Соответствующая свободная ячейка помечается знаком (+), и для нее в таблице метода потенциалов строится цикл. При этом циклом в таблице метода потенциалов называется ломаная, вершины которой расположены в занятых ячейках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое - в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами. При правильном построении таблицы допустимого решение для любой свободной ячейки можно построить лишь один цикл.
выбирается наименьшее значение (если их несколько- то любое из них). Соответствующая свободная ячейка помечается знаком (+), и для нее в таблице метода потенциалов строится цикл. При этом циклом в таблице метода потенциалов называется ломаная, вершины которой расположены в занятых ячейках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое - в столбце. Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами. При правильном построении таблицы допустимого решение для любой свободной ячейки можно построить лишь один цикл.
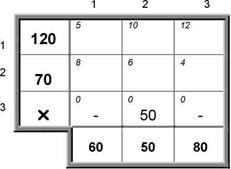
5. После того как построен цикл для выбранной свободной ячейки, следует рассчитать значения переменных нового допустимого решения. Для этого необходимо изменить значение переменных предыдущего допустимого решения в пределах ячеек, связанных с данной свободной ячейкой. Это изменение производят по следующим правилам:
· каждой ячейки, принадлежащей построенному циклу от выбранной свободной ячейки, приписывают определенный знак, причем свободной клетке – знак (+), а всем остальным клеткам – поочередно (+) и (-). Соответствующие ячейки называют также минусовыми и плюсовыми;
· в выбранную свободную ячейку записывают меньшее из чисел хij, стоящих в минусовых ячейках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых ячейках, и вычитают из чисел, стоящих в минусовых ячейках таблицы. При этом ячейка, которая ранее была свободной, становится занятой, а минусовая ячейка, в которой стояло минимальное из чисел хij , считается свободной.
В результате указанного изменения значений переменных в пределах ячеек, связанных циклом с данной свободной ячейкой, находится новое допустимое решение транспортной задачи, которому соответствует меньшее по сравнению с предыдущим решением значение целевой функции. После получения новой таблицы метода потенциалов следует прейти к выполнению действий этапа 3 настоящего алгоритма.
Рассмотренный алгоритм метода потенциалов может быть изображен графически в форме диаграммы деятельности языка UML.
В заключении следует отметить, что при определении начального допустимого решения или в процессе решения задачи может быть получено вырожденное решение. Чтобы избежать в этом случае зацикливания алгоритма, следует соответствующие нулевые элементы допустимого решения заменить сколь угодно малым положительным числом ε, после чего решать задачу как невырожденную. В оптимальном решении такой задачи необходимо считать ε равным нулю.
Для нахождения исходного допустимого решения транспортной задачи на этапе 2 алгоритма может быть использован так называемый метод минимального элемента. Сущность этого метода состоит в том, что начальное допустимое решение находится за п+т-1 шагов. При этом на каждом шаге находится значение только одной переменной хij, которая записывается в соответствующую ячейку. После чего данная ячейка становится занятой. Первоначально все ячейки таблицы свободные и среди них отыскивается такая ячейка, которой соответствует минимальное значение из коэффициентов целевой функции сij .Если таких ячеек несколько, то следует выбрать любую из них. Для найденной свободной ячейки определяется значение соответствующей переменной: хij = min{ai , bj}.
Заполнение выбранной ячейки обеспечивает полностью либо удовлетворение потребности в пункте потребления, если хij = bj = min{ai , bj }, либо вывоз всех запасов из пункта производства, если хij = ai = min{ai , bj}.
В первом случае исключают из дальнейшего рассмотрения столбец таблицы, соответствующий bj , а для i-й строчки полагают новое значение .Во втором случае исключают из дальнейшего рассмотрения строку соответствующую ai, а для j-го столбца полагают новое значение .
После исключения строки или столбца из дальнейшего рассмотрения происходит нахождение среди свободных ячеек следующего минимального значения сij и заполнение найденной ячейки очередным значением переменной: хij = min{ai , bj } с соответствующим исключением строки или столбца. В итоге после п+т-1 шагов метод минимального элемента позволяет получить начальное допустимое решение закрытой транспортной задачи линейного программирования.
Проиллюстрируем использование рассмотренного алгоритма метода потенциалов для решения индивидуальной транспортной задачи (2.6) и (2.7). Поскольку исходная задача является закрытой, то выполнение действий этапа 1 рассмотренного алгоритма метода потенциалов не требуется.
Исходная таблица метода потенциалов, необходимая для нахождения начального допустимого решения задачи (2.5) и (2.7), будет иметь следующий вид таблица 2.3.
Для нахождения начального допустимого решения воспользуемся методом минимального элемента. Для этого в таблице 2.3 следует найти минимальное значение сij , которое равно 1. этому значению соответствует второй пункт производства и первый пункт потребления, при этом х21 = min{a2 , b1 }=14. Из дальнейшего рассмотрения следует исключить второй пункт производства, а для первого пункта потребления определить новое значение b’=b1-a1=15-14=1.
Таблица 2.3. Исходная таблица для нахождения
начального допустимого решения
| F(x) | V1 15 | V2 12 | V3 8,5 | V4 5,5 |
| u1 10 | 3 | 5 | 7 | 11 |
| u2 14 | 1 | 4 | 6 | 3 |
| u3 17 | 5 | 8 | 12 | 7 |
На следующем шаге метода минимального элемента в сокращенной таблице таблица 2.3 найдем минимальное значение сij , которое равно 3. Этому значению соответствует первый пункт производства и первый пункт потребления, при этом х11 = min{a1 , b1 }=1. Из дальнейшего рассмотрения следует исключить первый пункт потребления, а для первого пункта производства определить новое значение a’=a1-b1=10-1=9.
Поступая аналогичным образом, в результате будет получено начальное допустимое решение транспортной задачи (2.6) и (2.7), исходная таблица метода потенциалов которой будет иметь следующий вид таблица 2.4.
Таблица 2.4. Исходная таблица метода потенциалов
с начальным допустимым решением
| F(x) | V1 15 | V2 12 | V3 8,5 | V4 5,5 |
| u1 10 | 3 1 | 5 9 | 7 | 11 |
| u2 14 | 1 14 | 4 | 6 | 3 |
| U3 17 | 5 | 8 3 | 12 8,5 | 7 5,5 |
Непосредственной проверкой можно убедиться, что найденное начальное решение действительно является допустимым. Этому начальному решению соответствует значение целевой функции:
F(x)=3*1+1*14+5*9+8*3+12*8,5+7*5,5=226,5
После выполнения подготовительных этапов 1 и 2 метода потенциалов можно приступить к проверке условия получения оптимального решения (этап 3). Для этого необходимо найти потенциалы пунктов производства и потребления. Поскольку число заполненных ячеек исходной таблицы равно п+т-1=6, то искомая система должна содержать п+т=7 неизвестных для 6 уравнений. А именно, для определения значений потенциалов следует решить следующую систему уравнений: {v1+u1=3, v1+u2=1, v2+u1=5, v2+u3=8, v3+u3=12, v4+u3=7}, содержащую шесть уравнений с семью неизвестными. Поскольку число неизвестных превышает на единицу число уравнений, то одно из неизвестных можно положить равным произвольному числу, например v1=0. Далее можно найти последовательно из данной системы уравнений значения остальных неизвестных: v2=2, v3=6, v4=1, u1=3, u1=2, u3=6.
На этом действия этапа 3 заканчиваются, а найденные значения потенциалов записываются в исходную таблицу, которая на первой итерации алгоритма будет иметь следующий вид таблица 2.5.
Таблица 2.5. Таблица метода потенциалов
на первой итерации
| F(x) | 0 15 | 2 12 | 6 8,5 | 1 5,5 |
| 3 10 | 3 1 | 5 9 | 7 | 11 |
| 1 14 | 1 14 | 4 | 6 | 3 |
| 6 17 | 5 | 8 3 | 12 8,5 | 7 5,5 |
Для выполнения этапа 4 алгоритма по формуле (2.11)необходимо последовательно рассчитать значения оценок для свободных ячеек:
![]() 7-3-6=-2,
7-3-6=-2, ![]() 4-1-2=1,
4-1-2=1,![]() 6-1-6=-1,
6-1-6=-1, ![]() 3-1-1=1,
3-1-1=1, ![]() 5-6-0=-1. Поскольку среди оценок свободных ячеек имеются отрицательные, то условие (2.12) не выполняется, и найденное решение не является оптимальным, т.е. его можно улучшить.
5-6-0=-1. Поскольку среди оценок свободных ячеек имеются отрицательные, то условие (2.12) не выполняется, и найденное решение не является оптимальным, т.е. его можно улучшить.
Из всех ![]() выбирается наименьшее значение
выбирается наименьшее значение ![]() -2. Соответствующая свободная ячейка для помечается знаком (*), и для нее х13 в таблице метода потенциалов строится цикл содержащий занятые ячейки: х12, х32, х33. После этого следует перейти к выполнению действий этапа 5.
-2. Соответствующая свободная ячейка для помечается знаком (*), и для нее х13 в таблице метода потенциалов строится цикл содержащий занятые ячейки: х12, х32, х33. После этого следует перейти к выполнению действий этапа 5.
Таблица 2.6. Таблица метода потенциалов
после выполнения первой итерации
| F(x)=209,5 | V1 15 | V2 12 | V3 8,5 | V4 5,5 |
| u1 10 | 3 1 | 5 0,5(-) | 7 8,5(+) | 11 |
| u2 14 | 1 14 | 4 | 6 | 3 |
| U3 17 | 5 | 8 11,5(+) | 12 (-) | 7 5,5 |
Поскольку ячейка для х13 имеет знак (+), то соседние с ней в цикле занятые ячейки х12 и х33 будут иметь знак (-). Следуя по правилу чередования знаков, оставшаяся ячейка х32 будет иметь знак (+). Наименьшее из чисел в минусовых ячейках равно 8,5.
Ячейка х33 , в которой находится это число, становится свободной в новой таблице метода потенциалов. Другие значения ячеек цикла в новой таблице получаются следующим образом: новое значение в минусовой ячейке равно: ![]() , новое значение в плюсовой ячейке равно:
, новое значение в плюсовой ячейке равно: ![]() .
.
В полученной таким образом новой таблице ячейка ![]() становится свободной. После выполненных на этапе 5 преобразований получаем новое допустимое решение транспортной задачи с лучшим значением целевой функции F(x)=209.5. Этому допустимому решению соответствует новая таблица метода потенциалов, которая имеет следующий вид, таблица 2.7.
становится свободной. После выполненных на этапе 5 преобразований получаем новое допустимое решение транспортной задачи с лучшим значением целевой функции F(x)=209.5. Этому допустимому решению соответствует новая таблица метода потенциалов, которая имеет следующий вид, таблица 2.7.
После получения таблицы 2.7 следует приступить к проверке условия получения оптимального решения (вторая итерация, этап 3).
Таблица 2.7. Метода потенциалов на
второй итерации
| F(x)=209,5 | 0 15 | 2 12 | 4 8,5 | 1 5,5 |
| 3 10 | 3 1 | 5 0,5 | 7 8,5 | 11 |
| 1 14 | 1 14 | 4 | 6 | 3 |
| 6 17 | 5 | 8 11,5 | 12 | 7 5,5 |
Для этого предварительно необходимо найти новые потенциалы пунктов производства и потребления. Для определения значений потенциалов следует решить следующую систему уравнений: {v1+u1=3, v1+u2=1, v2+u1=5, v2+u3=8, v3+u1=7, v4+u3=7}. Полагая v1=0, находятся значения остальных неизвестных: v2=2, v3=4 v4=1, u1=3, u2=1 u3=6.
На этом действия этапа 3 заканчиваются, а найденные значения потенциалов записываются в таблицу, которая на второй итерации алгоритма будет иметь следующий вид, таблица 2.7.
Для выполнения этапа 4 на второй итерации алгоритма по формуле (2.11) необходимо последовательно рассчитать значения для свободных ячеек: ![]() 11-3-1=-7,
11-3-1=-7, ![]() 4-1-2=1,
4-1-2=1,![]() 6-1-4=1,
6-1-4=1, ![]() 3-1-1=1,
3-1-1=1, ![]() 5-6-0=-1,
5-6-0=-1, ![]() 12-6-4=2.
12-6-4=2.
Поскольку среди оценок свободных ячеек имеется единственная отрицательная, то условие (2.12) не выполняется, и найденное решение не является оптимальным, т.е. его можно улучшить. Для единственного значения ![]() соответствующая свободная ячейка для х31 помечается знаком (+), и для нее в таблице метода потенциалов строится цикл, содержащий занятые ячейки: х11, х12,х32. После этого следует перейти к выполнению действий этапа 5 второй итерации.
соответствующая свободная ячейка для х31 помечается знаком (+), и для нее в таблице метода потенциалов строится цикл, содержащий занятые ячейки: х11, х12,х32. После этого следует перейти к выполнению действий этапа 5 второй итерации.
На этапе 5 необходимо определить плюсовые и минусовые ячейки. Поскольку ячейка для х31 имеет знак (+), то соседние с ней в цикле занятые ячейки х11 и х32 будут иметь знак (-). Следуя правилу чередования знаков, оставшаяся ячейка х12, будет иметь знак (+). Наименьшее из чисел в минусовых ячейках равно 1. Ячейка х11, в которой находится это число, становится свободной в новой таблице метода потенциалов. Другие значения ячеек цикла в новой таблице получаются следующим образом: новое значение в минусовой ячейке равно: x’32=x32-1=10.5, а новое значение в плюсовой ячейке равно: x’12=x12+1=1,5. В полученной таким образом новой таблице ячейка x’31=0 становится свободной. После выполненных на этапе 5 преобразований получаем новое допустимое решения транспортной задачи с лучшим значением целевой функции F(x)= 208.5. Этому допустимому решению соответствует новая таблица методов потенциалов, которая имеет следующий вид, таблица 2.8.
После получения таблицы 8 следует снова проверить условия получения оптимального решения (третья итерация, этап 3). Для этого необходимо найти новые потенциалы пунктов производства и потребления, т. е. решить следующую систему уравнений: {v1+u2=1, v1+u3=5, v2+u1=5, v2+u3=8, v3+u1=7, v4+u3=7}. Полагая v1=0, находятся значения остальных неизвестных: v2=3, v3=5 v4=2, u1=2, u2=1 u3=5. На этом действия этапа 3 заканчиваются, а найденные значения потенциалов записываются в таблицу, которая на третьей итерации алгоритма будет иметь следующий вид , таблица 9.
После получения таблицы 2.8 следует снова проверить условия получения оптимального решения (третья итерация, этап 3).
Для этого необходимо найти новые потенциалы пунктов производства и потребления, т. е. решить следующую систему уравнений: {v1+u2=1, v1+u3=5, v2+u1=5, v2+u3=8, v3+u1=7, v4+u3=7}. Полагая v1=0, находятся значения остальных неизвестных: v2=3, v3=5 v4=2, u1=2, u2=1 u3=5.
На этом действия этапа 3 заканчиваются, а найденные значения потенциалов записываются в таблицу, которая на третьей итерации алгоритма будет иметь следующий вид , таблица 2.9.
Таблица 2.8. Таблица метода потенциалов
после выполнения второй итерации
| F(x)=209,5 | V1 15 | V2 12 | V3 8,5 | V4 5,5 |
| u1 10 | 3 (-) | 5 1,5(-) | 7 8,5 | 11 |
| u2 14 | 1 14 | 4 | 6 | 3 |
| U3 17 | 5 1(+) | 8 10,5(-) | 12 | 7 5,5 |
Для выполнения этапа 4 на третьей итерации алгоритма по формуле (2.11) необходимо последовательно рассчитать значения оценок для свободных ячеек: ![]() 3-2-0=1,
3-2-0=1, ![]() 11-2-2=7,
11-2-2=7,![]() 4-1-3=0,
4-1-3=0, ![]() 6-1-5=0,
6-1-5=0, ![]() 3-1-2=0,
3-1-2=0, ![]() 12-5-5=2. Поскольку среди оценок свободных ячеек отсутствуют отрицательные значения, то условие (2.12) выполняется, и найденное решение является оптимальным.
12-5-5=2. Поскольку среди оценок свободных ячеек отсутствуют отрицательные значения, то условие (2.12) выполняется, и найденное решение является оптимальным.
Таблица 2.9. Таблица метода потенциалов
на третьей итерации
| F(x)=209,5 | 0 15 | 3 12 | 5 8,5 | 2 5,5 |
| 2 10 | 3 | 5 1,5 | 7 8,5 | 11 |
| 1 14 | 1 14 | 4 | 6 | 3 |
| 5 17 | 5 1 | 8 10,5 | 12 | 7 5,5 |
Таким образом, искомое оптимальное решение исходной транспортной задачи, полученное с использованием описанного алгоритма метода потенциалов, содержится в таблице9 и равно: х12=1,5, х13=8,5, х21=14, х31=1, х32=10,5, х34=5,5, значения остальных переменных равны 0. Оптимальное значение целевой функции при этом равно: F(x)=208.5.
Сравнение найденных оптимальных решений транспортной задачи с помощью программы MS Excel и метода потенциалов показывает их полное совпадение, что может свидетельствовать о достоверности соответствующих результатов.
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...
... ). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. · В ячейки E5:I5 - заявки на продукцию, ...

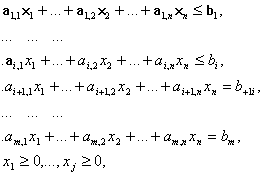
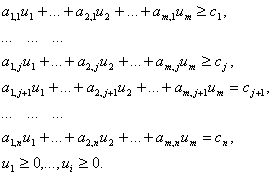


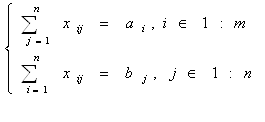
0 комментариев