Навигация
Рекомендации по решению задач оптимизации с
2.4 Рекомендации по решению задач оптимизации с
помощью надстройки Поиск решения.
Построение математической модели задачи.
Работа по решению некоторой оптимизационной задачи всегда начинается с построения математической модели, для чего необходимо ответить на следующие вопросы:
q Каковы переменные модели (для определения каких величин строится модель)?
q В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
q Каким ограничениям должны удовлетворять неизвестные?
Стоит также учесть, что при конструировании модели формулировка ограничений является самой ответственной частью конструкции. В некоторых случаях ограничения очевидны, например, ограничение на количество сырья. Другие же ограничения могут быть менее очевидны и могут быть указаны неверно. Например:
q В модели с несколькими периодами времени величина материального ресурса на начало следующего периода должна равняться величине этого ресурса на конец предыдущего периода;
q В модели поставок величина запаса на начало периода плюс количество полученного должна равняться величине запаса на конец период плюс количество отправленного;
q Многие величины в модели по своему физическому смыслу не могут быть отрицательными, например, количество полученных единиц товара.
Таким образом, на данном этапе делаются выводы об исходных данных (детерминировать или случайные), искомых переменных (непрерывные или дискретные), о пределах, в которых могут находиться значения искомых величин, о зависимостях между переменными (линейные или нелинейные), о критериях, по которым необходимо находить оптимальное решение. Сюда же входит преодоление несовместимости, а также неограниченности целевой функции: при максимизации целевой функции область допустимых решений должна быть ограничена сверху, при минимизации - ограничена снизу.
Решение задач с помощью надстройки Поиск решения.Прежде всего подготовьте рабочий лист MS Excel-корректно разместите на нем все исходные данные, грамотно введите необходимые формулы для целевой функции и для других зависимостей, выберите место для значений переменных.
Правильно выберите все ограничения, переменные, целевую функцию и другие значения в окно Поиск решения.
Большую часть задач оптимизации представляют собой задачи линейного программирования, т.е. такие, у которых критерий оптимизации и ограничения- линейные функции. В этом случае для решения задачи следует установить флажок Линейная модель в окне Параметры поиска решения. Это обеспечит применение симплекс-метода. В противном случае даже для решения линейной задачи будут использованы более общие (т.е. более медленные)методы.
Поиск решения может работать также и с нелинейными зависимостями и ограничениями. Это, как правило, задачи нелинейного программирования или, например, решение системы нелинейных уравнений. Для успешной работы средства Поиск решения следует стремиться к тому, чтобы зависимости были гладкими или, по крайней мере, непрерывными. Наиболее часто разрывные зависимости возникают при использовании функции ЕСЛИ(), среди аргументов которой имеются переменные величины модели. Проблемы могут возникнуть также и при использовании в модели функций типа ABS(), ОКРУГЛ() и т.д.
Решая задачи с нелинейными зависимостями, следует:
q Ввести предварительно предположительные значения искомых переменных (иногда легко получить графическое представление решение и сделать приблизительные выводы о решении).
q В окне Параметры поиска снять (если установлен) флажок Линейная модель.
Решая задачи целочисленного программирования, не следует забывать также о требованиях целочисленности и булевости.
Анализ решения задачи оптимизации.
При необходимости анализ решения. Часто добавляется также представление в виде графиков или диаграмм. Можно получить и отчет о поиске решения.
Отчеты бывают трех типов: Результаты, Устойчивость, Пределы.
Тип отчета выбирается по окончании поиска решения в окне Результаты поиска решения в списке Тип отчета (можно выбрать сразу два или три типа).
q Отчет типа Результаты содержит окончательные значения параметров задачи целевой функции и ограничений.
q Отчет типа Устойчивость показывает результаты малых изменений параметров поиска решения.
q Отчет типа Пределы показывает изменения решения при поочередной максимизации и минимизации каждой переменной при неизменных других переменных.
Линейная оптимизация.
Линейное программирование-это раздел математического программирования, посвященный нахождению экстремума линейных функций нескольких переменных при дополнительных линейных ограничениях, которые налагаются на переменные. Методы, с помощью которых решаются задачи, подразделяются на универсальные (например, симплексный метод) и специальные. С помощью универсальных методов решаются любые задачи линейного программирования. Особенностью задач линейного программирования является то, что экстремум целевой функции достигается на границе области допустимых решений.
Пример. Планирование производства материалов.
Фирма выпускает два типа строительных материалов: А и В. продукция обоих видов поступает в продажу. Для производства материалов используются два исходных продукта:1 и 2. Максимально возможные суточные запасы этих продуктов составляют 7 и 9 тонн соответственно. Расходы продуктов 1 и 2 на 1 тонну соответствующих материалов приведены в табл. 7.4.
Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 тонну. Кроме того, спрос на материал А никогда не превышает 3 тонн в сутки. Оптовые цены одной тонны материалов равны: 4000 у.е. для В и 3000 у.е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?
Таблица 2.10. Расход продуктов
| Исходный продукт | Расход исходных продуктов, т (на одну тонну материалов) | Максимально Возможный запас, т | |
| Материл А | Материал В | ||
| 1 | 3 | 2 | 7 |
| 2 | 2 | 3 | 9 |
Решение
1. Формулировка математической задачи:
· переменные для решения задачи: х1- суточный объём производства материала А, х2- суточный объём производства материала В;
· определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства х1 материала А и х2 материала В равна:
F=4000x2+3000x1
поэтому цель фабрики- среди всех допустимых значений х2 и х1 найти такие, которые максимизируют суммарную прибыль от производства материалов F:
F=4000x2+3000x1àmax;
· ограничения на переменные:
q объём производства красок не может быть отрицательным, т.е.
х2![]() 0, х1
0, х1![]() 0;
0;
q расход исходного продукта для производства обоих видов материалов не может превосходить максимально возможного запаса данного исходного продукта, т.е.:
2х2+3х1![]() 7,
7,
3х2+2х1![]() 9,
9,
q ограничения на величину спроса на материалы:
х1-х2![]() 1,
1,
х1![]() 3,
3,
· Найти максимум следующей функции:
F=4000x2+3000x1àmax,
· При ограничениях вида:
2х2+3х1![]() 7,
7,
3х2+2х1![]() 9,
9,
х1-х2![]() 1,
1,
х1![]() 3,
3,
х2![]() 0, х1
0, х1![]() 0;
0;
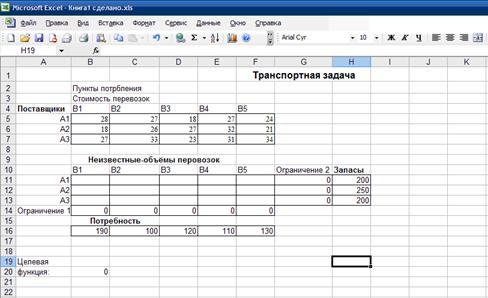
2.Подготовка листа рабочей книги MS Excel для вычислений- на рабочий лист вводим необходимый текст, данные и формулы в соответствии с рис. 7.3. Переменные задачи х1 и х2 находятся, соответственно, в ячейках С3 и С4. Целевая функция находится в ячейке С6 и содержит формулу:
=4000*С4+3000*С3.
Ограничения на задачу учтены в ячейках С8:D11.
Рисунок 2. Рабочий лист MS Excel для решения задачи
 планирования производства материалов
планирования производства материалов
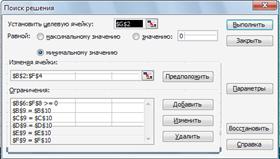
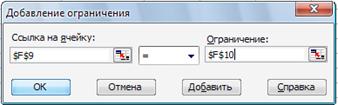
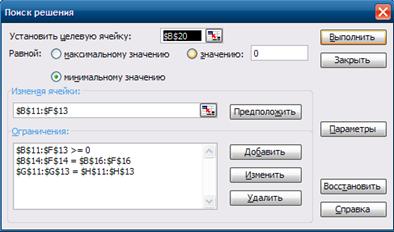
3.Работа с надстройкой Поиск решения- воспользовавшись командой Сервис \ Поиск решения, вводим необходимые данные для рассматриваемой задачи (установка данных в окне Поиск решения приведена на рисунке 2). Результат работы по поиску решения помещен на рисунке 2
Рисунок 2. Установка необходимых параметров задачи
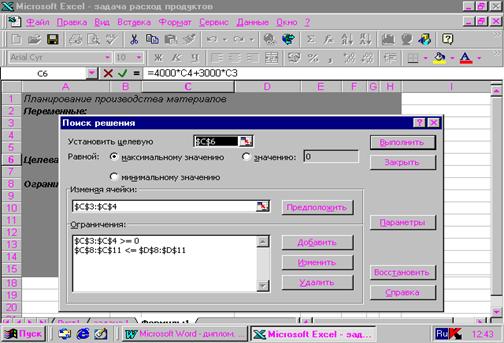 планирования материалов в окне Поиск решения
планирования материалов в окне Поиск решения
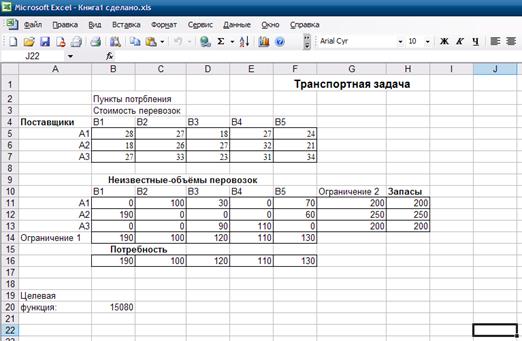
Рисунок 2. Результат расчета надстройки Поиск решения
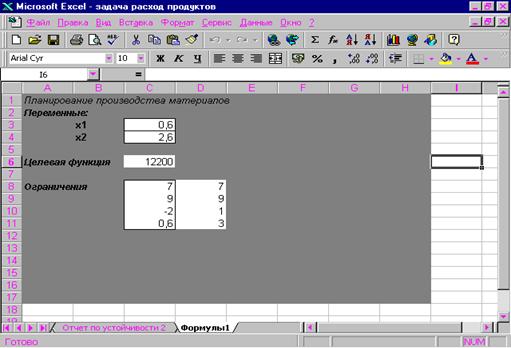
Рисунок 2. Отчета по результатам Поиска решения

Описание отчетов о решении задачи
q Отчет по результатам –таблица Целевая ячейка выводит сведения о целевой функции; таблица Изменяемые ячейки показывает значение искомых переменных, полученных в результате решения задачи; таблица Ограничения отображает результаты оптимального решения для ограничений и для граничных условий. В поле Формула приведены зависимости, которые были введены в окно Поиск решения, в поле Разница- величина использованного материала. Если материал используется полностью, то в поле Статус указывается связанное, при неполном использовании материала в этом поле указывается не связан. Для граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины с той лишь разницей, что вместо величины неиспользованного продукта показана разность между значением переменой в найденном оптимальном решении и заданным для неё граничным условием.
q Отчет по устойчивости –в таблице Изменяемые ячейки приводится результат решения задачи.
В таблице Ограничения выводятся значения для ограничений, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
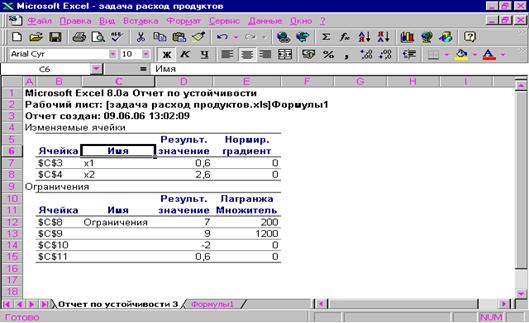 Рисунок 2. Отчет по устойчивости Поиска решения
Рисунок 2. Отчет по устойчивости Поиска решения
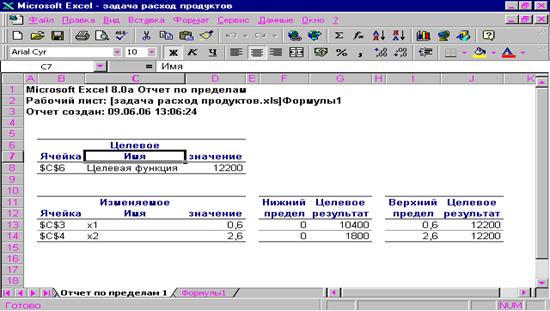
q Отчет по пределам- в отчете показано, в каких пределах может изменяться количество материалов, вошедших в оптимальное решение, при сохранении структуры оптимального решения; приводятся значение переменных в оптимальном решение, а также нижние и верхние пределы изменения значений переменных; здесь также указаны значения целевой функции при выпуске данного типа продукции на верхнем и нижнем пределах.
Глава III Двойственная задача линейного программирования
3.1 Математическая формулировка двойственной задачи линейного программирования
В общем случае двойственной по отношению к стандартной задаче линейного программирования (1.6) и (1.7) называется такая задача линейного программирования, которая может быть записана в следующем виде:
b1y1+b2y2+,…,+bmym →![]() (3.1)
(3.1)
где множество допустимых альтернатив ![]() формируется следующей системой ограничений типа неравенств:
формируется следующей системой ограничений типа неравенств:
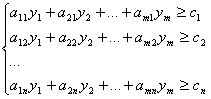 (3.2)
(3.2)
и y1,y2,,…,yn![]() 0.
0.
Как не трудно заметить, количество переменных двойственной задаче линейного программирования равно количеству ограничений стандартной задачи, а количество ограничений двойственной задачи равно количеству переменных стандартной задачи линейного программирования. При этом, если исходная задача формулируется как задача максимизации целевой функции, то двойственная- как задача минимизации и наоборот. Аналогично изменяются и знаки ограничений двойственной задачи по отношению к исходной задаче линейного программирования.
Существует важная взаимосвязь между двойственной и стандартной задачами линейного программирования. А именно, если одна из задач (1.6) и (1.7) или (3.1) и (3.2) имеет оптимальное решение, то и двойственная ей задача линейного программирования имеет оптимальное решение, при этом оптимальные значения соответствующих целевых функций двойственных задач имеют равные значения, т.е. f’op=fopt , где f’(y)- целевая функция в выражении (3.1), а f(x)–целевая функция в выражении (1.6). Если же для одной из задач (1.6) и (1.7) или (3.1) и (3.2) целевая функция не ограничена на допустимом множестве альтернатив, то соответствующая ей двойственная задача линейного программирования не имеет решения, т.е. имеет множество допустимых альтернатив. Наконец, если одна из задач (1.6) и (1.7) или (3.1) и (3.2) имеет пустое множество допустимых альтернатив, то соответствующая ей двойственная задача линейного программирования либо имеет неограниченную целевую функцию, либо пустое множество допустимых альтернатив.
В общем случае совместное рассмотрение пары двойственных задач линейного программирования позволяет не только выполнить качественный анализ их решения, но и практически использовать найденное решение одной из них для более простого решения другой задачи. Хотя данное свойство оказывается полезным, главным образом, при выполнении ручных расчетов, далее рассмотрим процесс решения двойственных задач линейного программирования с помощью программы MS Excel применительно к задаче о красках.
Похожие работы
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...
... ). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий. §4. Решение транспортной задачи в Excel В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов. · В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах. · В ячейки E5:I5 - заявки на продукцию, ...

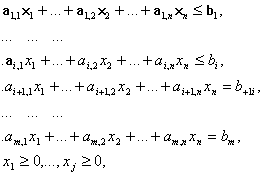
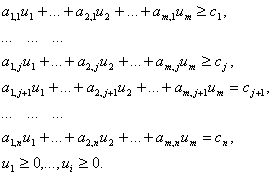


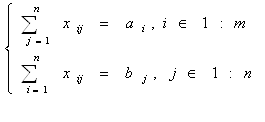
0 комментариев