Навигация
Графический метод решения игровых задач с нулевой суммой
3. Графический метод решения игровых задач с нулевой суммой
Суть графического метода состоит в том, что из матрицы удаляют дублирующие и поглощаемые строки и столбцы. Дублирующими называют полностью одинаковые строки или столбцы. Доминирующей строкой называется такая строка, которая содержит элементы, большие или равные соответствующим элементам другой строки, называемой поглощаемой. Доминирующим столбцом называется такой, который содержит элементы, меньше или равные соответствующим элементам другого столбца, который называется поглощаемым.
Воспользуемся табл. 2.1.
Строка (стратегия) А1 является доминирующей по отношению к строке (стратегии) А4 , так как содержит элементы, большие соответствующих элементов строки А4 . Соответственно строка А4 является поглощаемой и из дальнейшего рассмотрения удаляется (табл. 3.1).
Таблица 3.1
Первый шаг упрощения таблицы
| Стратегии | В1 | В2 | В3 | В4 | В5 |
| А1 | 5 | 8 | 7 | 5 | 4 |
| А2 | 1 | 10 | 5 | 5 | 6 |
| А3 | 2 | 4 | 3 | 6 | 2 |
Первый столбец является доминирующим по отношению ко второму, третьему и четвертому столбцам (поглощаемым). Поступаем аналогично (табл. 3.2).
Таблица 3.2
Второй шаг упрощения таблицы
| Стратегии | В1 | В5 |
| А1 | 5 | 4 |
| А2 | 1 | 6 |
| А3 | 2 | 2 |
Еще раз рассматриваем строки. Первая строка поглощает третью строку. Поглощаемые строки (столбцы) содержат самые плохие стратегии. Окончательно получим (табл. 3.3).
Таблица 3.3
Третий шаг упрощения таблицы
| Стратегии | В1 | В5 |
| А1 | 5 | 4 |
| А2 | 1 | 6 |
Вероятность использования первой фирмой первой стратегии обозначим через p1. Тогда вероятность использования второй стратегии первым игроком будет p2 = 1- p1 . Ожидаемый выигрыш фирмы А от применения
![]() (3.1)
(3.1)
вторым игроком первой стратегии составит:
Аналогичным способом получим ожидаемый выигрыш фирмы А от применения вторым игроком:
![]() (3.2)
(3.2)
В выражения (3.1) и (3.2) подставим конкретные значения.
![]()
![]()
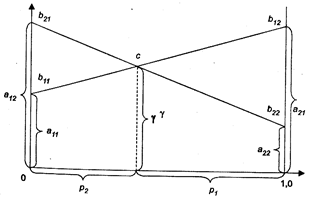
На оси х отложим две точки 0 и 1. Через эти точки проведем прямые линии, параллельные оси у. Затем в первое выражение подставим 0 вместо p1, а потом – единицу. И по двум точкам построим прямую линию.
Аналогично построим вторую прямую линию. Пересечение двух прямых линий и даст решение задачи (рис. 3.1).
| | ||||
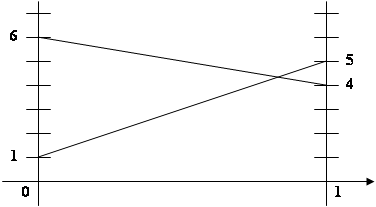 | ||||
Рис. 3.1 . Графический способ определения стратегий фирмы А
4p1 + 1= - 2p1 + 6
4p1 + 2p1 = - 1 + 6
6p1 = 5
p1 = 0,83
Итак, вероятность использования первой стратегии фирмой А составляет 0,83 (p1 = 0,83), а второй стратегии p2 = 1 – 0,83 – соответственно 0,17 (p2 = 0,17).
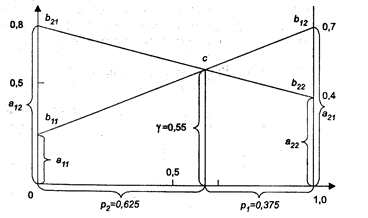
Аналогично определим оптимальную стратегию поведения фирмы В:
Пусть у1 – вероятность выбора второй игрой 5 стратегией, у2 - 6 стратегией. (p4 + p5 = 1, p5 = 1- p4)
(a11 – a12) · у1 + a12 = (5 – 4) у1 + 4 = у1 + 4;
(a21 – a22) · у1 + a22 = (1 – 6) у1 + 6 = -5 у1 + 6.
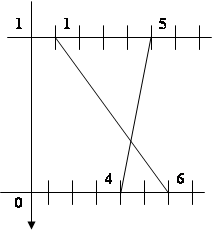
Рис. 3.2 . Графический способ определения стратегий фирмы В
у1 + 4 = -5 у1 + 6
6 у1 = 2
у1 = 0,33
Вероятность использования первой стратегии фирмой В составляет 0,33 (у1 = 0,33), а второй стратегии у2=1- 0,33 – соответственно 0,67 (у2 = 0,67).
Похожие работы
... систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур. Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
... запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы ...
... , находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания: или 8.Среднее число свободных обслуживающих каналов . 9.Коэффициент простоя обслуживающего канала: II. Практическое применение теории игр в задачах моделирования экономических процессах Пример №1 На базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен ...


0 комментариев