Навигация
4.1 Решение задач
Пример 5: Найти решение игры, определяемой матрицей.
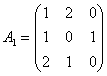
Решение.
Составим теперь пару взаимно-двойственных задач :
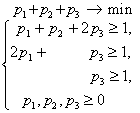

Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
|
| -1 | -1 | -1 | 0 | 0 | 0 | 0 | -3 | |
|
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | — |
| q5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | — |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
|
| 0 | -1 | 0 | 0 | 1 | 0 | 1 | 1 | |
|
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | — |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
|
| | 0 | 0 | | 1 | 0 | | | |
| q2 | | 1 | 0 | | 0 | 0 | | | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | | 0 | 0 |
| 0 | 1 | | |
Из оптимальной симплекс-таблицы следует, что![]()
(q1, q2, q3) = (0;![]() ; 1),
; 1),
а из соотношений двойственности следует, что
( p1, p2, p3) = (![]() ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
![]() .
.  ,
,
а игры с платёжной матрицей А:
![]() .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = ![]() =
= ![]()
Y = (y1, y2, y3) = (uq1; uq2; uq3) = ![]() =
= ![]() .
.
5. Игры с природой (без противодействия)
В играх с противодействием фирме А (одному игроку) противостоит другая фирма – В (игрок). Фирма В выбирает целенаправленную стратегию поведения с тем, чтобы уменьшить выигрыш фирмы А (следовательно, и свой проигрыш).
В играх с природой вторым игроком является природа, которая действует («выбирает» стратегии) случайным образом. То есть она может или улучшать положение первого игрока, или ухудшать. Поэтому существует несколько критериев оценки результатов исследования игровой модели.
1. Критерий Вальде (пессимистический).
В соответствии с этим критерием следует применять самую осторожную стратегию, которая сведет к минимуму вероятность (риск) проигрыша и доставит минимальную прибыль. Эта стратегия обеспечивается критерием:
max (min a ij ).(5.1)
где минимум выбирается по каждой строке.
То есть этот критерий совпадает с нижней ценой игры.
2. Критерий максимума (оптимистический).
Этот критерий полагает, что природа будет максимально благосклонна к игроку. Можно выбирать самые авантюристические стратегии и они будут реализоваться
max (max a ij ).(5.2)
где максимум выбирается по каждой строке.
Похожие работы
... систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур. Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
... запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы ...
... , находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания: или 8.Среднее число свободных обслуживающих каналов . 9.Коэффициент простоя обслуживающего канала: II. Практическое применение теории игр в задачах моделирования экономических процессах Пример №1 На базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен ...


0 комментариев