Навигация
3. Критерий Гурвица.
Критерий Гурвица занимает промежуточное значение между критерием Вальде и критерием максимума. Сам игрок определяет вероятность своего «везения»
max (α min a ij + (1- α) max a ij ) .(5.3)
Ответственное лицо, принимающее решение, определяет значение коэффициента α. Если потери могут быть весьма значительными, то значение коэффициента α приближается к единице, иначе к 0.
4. Критерий Сэвиджа.
Этот критерий анализирует возможные риски от применения каждой из стратегий и выбирает такую стратегию, которая обеспечивает приемлемые потери. Риски по каждой стратегии определяются по формуле:
r ij = max a ij - a ij.(5.4)
То есть из максимально возможного выигрыша при данном состоянии природы вычитается выигрыш, полученный от использования выбранной стратегии. Каждый элемент матрицы рисков обозначает потери, которые понесет фирма (точнее, недополученную прибыль), если для каждого текущего состояния природы будет выбрана неоптимальная стратегия. Оптимальная стратегия может быть определена по формуле:
min (max (max a ij - a ij).(5.5)
где максимум выбирается в каждом конкретном столбце.
Для примера возьмем таблицу стратегий (табл. 5.1) и составим для нее таблицу рисков (табл. 5.2).
Если фирма (игрок) выберет стратегию А1, а природа реализует стратегию В1 , то фирма получит максимально возможную прибыль 5 (недополученная прибыль составит 0). Фирма угадала состояние природы. Но если природа реализует стратегию В4, то фирма вместо максимально возможной прибыли 12 получит прибыль 5, а недополученная прибыль составит 7.
Таблица 5.1
Таблица стратегий
| Стратегии | В1 | В2 | В3 | В4 | В5 |
| А1 | 5 | 8 | 7 | 5 | 4 |
| А2 | 1 | 10 | 5 | 5 | 6 |
| А3 | 2 | 4 | 3 | 6 | 2 |
| А4 | 3 | 5 | 4 | 12 | 3 |
| max a ij | 5 | 10 | 7 | 12 | 6 |
Таблица 5.2
Таблица рисков
| Стратегии | В1 | В2 | В3 | В4 | В5 |
| А1 | 0 | 2 | 0 | 7 | 2 |
| А2 | 4 | 0 | 2 | 7 | 0 |
| А3 | 3 | 6 | 4 | 6 | 4 |
| А4 | 2 | 5 | 3 | 0 | 3 |
5.1 Решение задач
Пример 1: Швейная фабрика на летний сезон может реализовать два вида костюмов: 1200 костюмов по цене 520 руб. и 200 костюмов по цене 1000 руб., если погода будет жаркой. Если погода будет холодной, то фабрика может реализовать 650 костюмов первого вида и 700 костюмов второго вида.
Определить план выпуска костюмов каждого вида и прибыль, полученную от их реализации.
Решение:
Швейная фабрика располагает двумя стратегиями: А1 - погода будет жаркой и А2 – погода будет холодной.
Если фабрика воспользуется первой стратегией и погода действительно будет жаркой, то прибыль фабрики составит:
1200 · 520 + 200 · 1000 = 624 000 + 200 000 = 824 000 руб.
Если фабрика воспользуется первой стратегией, но погода будет холодной, то прибыль фабрики составит:
650 · 520 + 200 · 1000 – (1200 – 650) · 520 = 338 000 + 200 000 – 286 000 = 252 000 руб.
Если фабрика воспользуется второй стратегией и погода действительно будет холодной, то прибыль фабрики составит:
650 · 520 + 700 · 1000 = 338 000 + 700 000 = 1 038 000 руб.
Если фабрика воспользуется второй стратегией, но погода будет жаркой, то прибыль фабрики составит:
650 · 520 + 200 · 1000 – (700 – 200) · 1000 = 338 000 + 200 000 – 500 000 = 38 000 руб.
Составим матрицу прибыли (таб. 5.3).
Таблица 5.3
Матрица прибыли
| Стратегии | В1 | В2 |
| А1 | 824 000 | 252 000 |
| А2 | 38 000 | 1 038 000 |
α = max (252 000; 38 000) = 252 000 руб.
β = min (824 000; 1 038 000) = 824 000 руб.
Таким образом, цена игры находится в диапазоне от 252 000 руб. до 824 000 руб.
Минимальный гарантированный доход швейной фабрики составит 252 000 руб., но возможен и доход в 824 000 руб.
Определим план выпуска изделий швейной фабрикой. Вероятность выбора стратегии А1 обозначим через х1, а вероятность выбора стратегий А2 – через х2. Учитывая, что х2 = 1 - х1,можем записать:
(a11 – a12)· х1 + a12 = (824 000 – 38 000)· х1 + 38 000 = 786 000 х1 + 38 000;
(a21 – a22)· х1 + a22 = (252 000 – 1 038 000) · х1 + 1 038 000 = -786 000 х1 + 1 038 000;
786 000 х1 + 786 000 х1 = 1 038 000 – 38 000
1 572 000 х1 = 1 000 000
х1 = 0,64; х2 = 1 – 0,64х2 = 0,36;
0,64 (1200; 200) + 0,36 (650; 700) = (1002; 380).
Цена игры составит: 786 000 х1 + 38 000 = 541 040 руб.
Таким образом, план выпуска изделий таков: 1002 костюма первого вида и 380 костюмов второго вида, и при любых погодных условиях швейная фабрика получит прибыль не менее 541 000 руб.
Определим критерии.
1. Критерий Вальде:
max (min a ij) = max (38 000; 252 000) = 252 000 руб.
Швейной фабрике целесообразно использовать стратегию А1 .
2. Критерий максимума:
max (max a ij ) = max (824 000; 1 038 000) = 1 038 000 руб.
Швейной фабрике целесообразно использовать стратегию А2 .
3. Критерий Гурвица:
пусть α = 0,4 , тогда для стратегии А1
α min a ij + (1 - α) max a ij = 0,4 · 252 000 + (1 – 0,4) · 824 000 = 595 200 руб.
для стратегии А2
α min a ij + (1 - α) max a ij = 0,4 · 38 000 + (1 – 0,4) · 1 038 000 = 638 000 руб.
Швейной фабрике целесообразно использовать стратегию А2 .
4. Критерий Сэвиджа:
Максимальный элемент в первом столбце – 824 000, во втором столбце – 1 038 000.
Матрица рисков будет иметь вид:
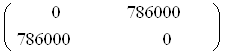
Швейной фабрике целесообразно использовать стратегию А1 или А2 .
Заключение
При написании курсовой работы по дисциплине «Математические методы» на тему «Теория игр» у меня возникли проблемы с теоретической частью курсовой работы. Мне приходилось брать одну литературу и искать нужную информацию, а потом, если в ней не полностью раскрыта тема, то брал следующую, а в ней более труднее приходилось разбираться, так как один автор пишет, как он понимает, а другой - свои взгляды на тему. Но я смог преодолеть эту непреодолимую пропасть.
Список литературы
1. « Математические методы в программировании » : / Агальцов В.П., Волдайская И.В. Учебник : – М . : ИД «ФОРУМ» : ИНФРА-М, 2006. – 224с. : ил. –(Профессиональное образование). – (Учимся программировать).
2. Лекции по дисциплине « Математические методы ».
3. «Математические методы: Учебник» / Партика Т.Л., Попов И.И. – М: ФОРУМ: ИНФРА, 2005.
4.«Математическое программирование» / Костевич Л., издательство «Новое знание», 2003.
Похожие работы
... систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур. Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
... запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы ...
... , находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания: или 8.Среднее число свободных обслуживающих каналов . 9.Коэффициент простоя обслуживающего канала: II. Практическое применение теории игр в задачах моделирования экономических процессах Пример №1 На базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен ...


0 комментариев