Решение задач графическим методом

3.1 Решение задач графическим методом

Пример 1: Рассмотрим игру заданной платежной матрицей:

	4×5

Решение:

Проверим есть ли седловая точка :

α = max (2,2,3,2) = 3

β = min (7,6,6,4,5) = 4 α ≠ β

Седловой точки нет, игра в чистых стратегиях не решается. Найдем смешанную стратегию игроков. Посмотрим, можно ли удалить не выгодную стратегию для игроков. Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.

Невыгодные стратегии для первого игрока:	4, 2
Невыгодные стратегии для второго игрока:	1, 2, 3

						p1
					1 – p1
	p4

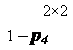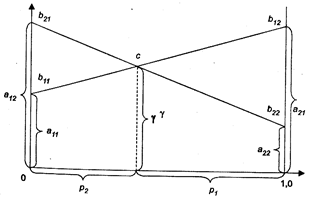
Пусть p₁ – вероятность с которой первый игрок должен применять 1 стратегию, p₃ – вероятность применения 3 стратегией, p₃ = 1- p₁ .

Ожидаемый выигрыш 1 игрока, если второй выбрал 4 стратегию:

p1 · 4 + (1 - p1) · 3 = p1 + 3;

Ожидаемый выигрыш 1 игрока, если второй выбрал 5 стратегию:

p1 · 2 + (1 - p1) · 5 = -3 p1 + 5;

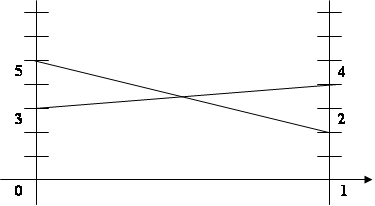
p₁ + 3 = -3 p₁ + 5

4 p₁ = 2

p₁ = 1/2 , p₃ =1/2 .

Первому игроку для получения гарантированного выигрыша 3,5 (1/2+3) рекомендуется чередовать стратегии 1 и 3.

Рассмотрим второго игрока.

Пусть p4 – вероятность выбора вторым игроком 4 стратегией, p5 - 5 стратегией. (p4 + p5 = 1, p5 = 1- p4)

Ожидаемые проигрыш второго игрока, если первый выберет 1 стратегию.

p4 · 4 + (1- p4) · 2 = 2 p4 + 2

Ожидаемые проигрыш второго игрока, если первый выберет 3 стратегию.

p4 · 3 + (1- p4) · 5 = -2 p4 + 5

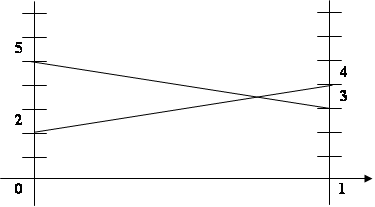
2 p₄  + 2 = -2 p₄  +5

4 p₄  =3

p₄  =3/4

p₅  =1/4

ν = 3/4 · 2 + 2 = 3,5

Ответ : Из 4 игр 3 надо сыграть 4 стратегией, 1 игру – 5 стратегией, и тогда проигрыш будет не больше 3,5, для первого игрока 1 надо сыграть 2 стратегией и 1 – второй стратегией.

Пример 2: Решить игру, заданную матрицей

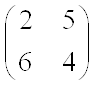
Решение:

Проверим если ли седловая точка:

α = max (2,4) = 4

β = min (6,5) = 5 α ≠ β

седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков. Т.к. игровая матрица задана первоначально в размерности 2×2, значит убирать столбцы или строки не нужно.

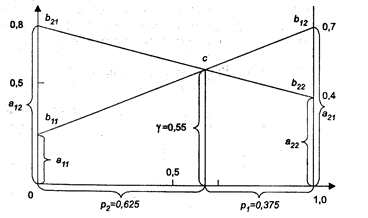
Ожидаемый выигрыш 1 игрока если второй выбрал 1 стратегию:

А1 · 2 + (1 - А1) · 6 = -4А1 + 6;

Ожидаемый выигрыш 1 игрока если второй выбрал 2 стратегию:

А1 · 5 + (1 - p1) · 4 = А1 + 4;

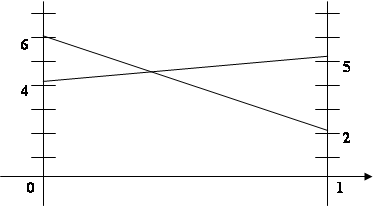
- 4 А₁ + 6 = А₁ + 4

- 4 А₁ + А₁ = 4 – 6

- 5 А₁ = - 2

А₁ = 2/5 , А₂ = 3/5.

Первому игроку для получения гарантированного выигрыша 4,

(2/5+4) рекомендуется играть 1 стратегией.

Рассмотрим второго игрока.

Пусть В1 – вероятность выбора второй игрой 4 стратегией,

(В1 + В2 = 1, В2 = 1- В1)

Ожидаемый проигрыш второго игрока, если первый выберет 1 стратегию.

В1 · 2 + (1- В1) · 5 = - 3 В1 + 5

Ожидаемый проигрыш второго игрока, если первый выберет 2 стратегию.

В1 · 6 + (1- В1) · 4 = 2 В1 + 4

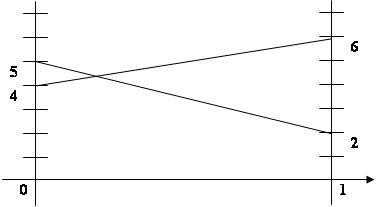
- 3 В₁ + 5 = 2 В₁ + 4

- 3 В₁ – 2 В₁ = 4 – 5

- 5 В₁ = - 1

В₁ = 1/5 , В₂ = 4/5.

ν = 1/5 · 2 + 4 = 4

Ответ : Из 2 игр 2 надо сыграть 1 стратегией, 1 игру – 2 стратегией, и тогда проигрыш будет не больше 4.

Пример 3: Решить игру, заданную матрицей

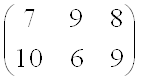
Проверим если ли седловая точка:

α = max (7,6) = 7

β = min (10,9,9) = 9 α ≠ β

седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков. Посмотрим, можно ли удалить не выгодную стратегию для игроков. Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.

Невыгодная стратегия для второго игрока:

3

p1

				1 – p1
	p4		1 – p4

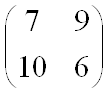
Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:

 p₁ · 7 + (1 - p₁) · 10 = -3p₁ + 10;

 

Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:

p1 · 9 + (1 - p1) · 6 = 3 p1 + 6;

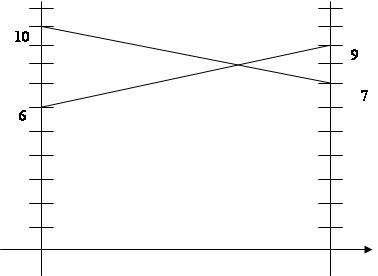
-3p₁ + 10 = 3 p₁ + 6

 -3p₁ - 3p₁ = -10 + 6

 -6p₁ = -4

p₁ = 2/3 , p₂ =1/3 .

Первому игроку для получения гарантированного выигрыша 7, (2/3+7) рекомендуется играть 1 стратегией.

Рассмотрим второго игрока.

Ожидаемые проигрыш второго игрока если первый выберет 1 стратегию.

p4 · 7 + (1- p4) · 9 = -2 p4 + 9

Ожидаемые проигрыш второго игрока если первый выберет 2 стратегию.

p4 · 10 + (1- p4) · 6 = 4 p4 + 6

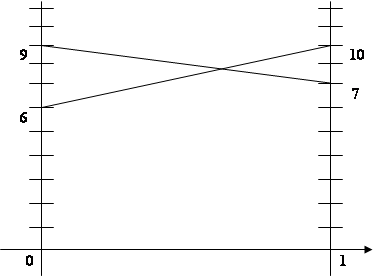
-2p₄ + 9 = 4 p₄ + 6

 -2p₄ - 4p₄ = 6 – 9

 -6p₄ = -3

р₄ = 1/2 , p₅ =1/2 .

Ответ : Из 2 игр (для первого) 2 надо сыграть 3 стратегией и 1 – 3 стратегией, (для второго) 1 надо сыграть 2 стратегией и 1 – 2 стратегией.

Пример 4: Решить игру, заданную матрицей

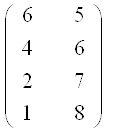
Проверим если ли седловая точка:

α = max (5,4,2,1) = 5

β = min (6,8) = 6 α ≠ β

седловой точки нет, игра в чистой стратегии не решается. Найдем смешанную стратегию игроков.

Посмотрим можно ли удалить не выгодную стратегию для игроков Для первого игрока невыгодной считается та стратегия, которая, обеспечивает выигрыш меньший, чем какая либо другая. Для второго игрока считается та стратегия не выгодной, которая обеспечить проигрыш больший, чем другая стратегия.

Невыгодная стратегия для первого игрока:

2,3

					p1
					1 - p1
	р4		1 – p4

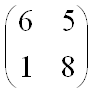
Ожидаемый выигрыш 1 игрока, если второй выбрал 1 стратегию:

 

p₁ · 6 + (1 - p₁) · 1 = 5 p₁ + 1;

Ожидаемый выигрыш 1 игрока, если второй выбрал 2 стратегию:

 

p₁ · 5 + (1 - p₁) · 8 = -3 p₁ + 8;

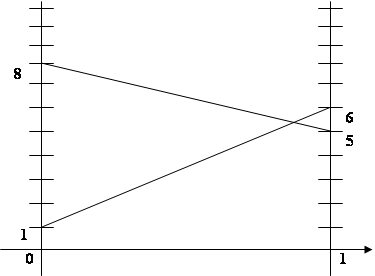
5 p₁ + 1 = -3 p₁ + 8

 5 p₁ + 3p₁ = 8 – 1

 8 p₁ = 7

p₁ = 7/8 , p₂ =1/8 .

Рассмотрим второго игрока.

Ожидаемые проигрыш второго игрока, если первый выберет 1 стратегию.p4 · 6 + (1- p4) · 5 = p4 + 5

Ожидаемые проигрыш второго игрока, если первый выберет 2 стратегию.

p4 · 1 + (1- p4) · 8 = -7 p4 + 8

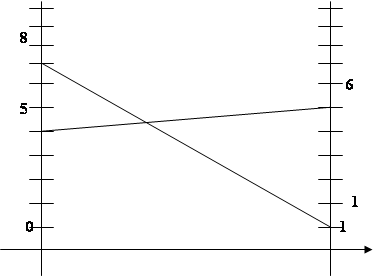
p₄ + 5 = -7 p₄ + 8

 p₄ + 7 p₄ = 8 – 5

 8 p₄ = 3

р₄ = 3/8 , p₅ =5/8 .

 u = .

Ответ : Из 4 игр (для первого) 7 надо сыграть 8 стратегией и 1 – 8, (для второго) 3 надо сыграть 8 стратегией и 5 – 8.