Дифференциальное уравнение заданной САУ

2.5 Дифференциальное уравнение заданной САУ

Получим ДУ заданной САУ:

2.6 Нормальная форма Коши, полученного ДУ 3-го порядка

Так как ДУ заданной САУ имеет высокий порядок, то его необходимо свести к системе уравнений, каждое из которых должно иметь первый порядок, т.е. имеет место нормальная форма Коши:

. (9)

Так как ДУ заданной САУ имеет укороченную правую часть, то запишем нормальную форму Коши в следующем виде:

. (10)

Приведём уравнение (12) к нормальной форме Коши:

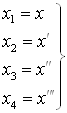(11)

или

,

 где

 

2.7 Аналитическое решение ДУ

Пусть задано изображение выхода

или .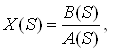

Тогда используя вторую теорему разложения Лапласа 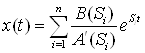получим следующее аналитическое выражение для выходного сигнала:

реакция системы на единичное ступенчатое воздействие () (12):

(12)

 

2.8 Решение ДУ численным методом(метод Рунге-Кутта 5-го порядка и метод Адамса неявный 4-го порядка)

В неявных методах используется информация о возможном будущем значении решения в точке п+1. Это несколько повышает точность получаемых результатов по сравнению с явными методами.

Для организации вычислительного процесса по интерполяционной формуле Адамса, имеющей точность решения (13):

необходимо заготовить начальные значения , используя метод Рунге-Кутта 5-его порядка.

Приведенные коэффициенты:

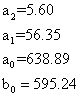
Проведём исследование решения ДУ в зависимости от шага:

Графики выходного сигнала, полученного в аналитическом виде , выходного сигнала, полученного решением ДУ и ошибки решения при шаге h=0.1 и h=0.01, h=0.001.

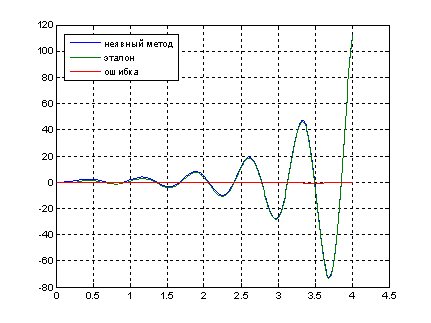
Рис.7. Графики выходного сигнала , полученного в аналитическом виде, выходного сигнала , полученного численным решением ДУ и ошибки решения при шаге

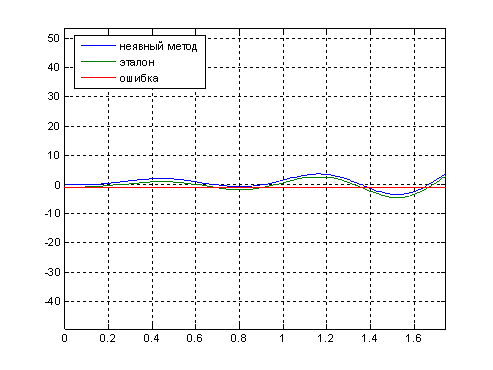
Рис.8. Графики выходного сигнала , полученного в аналитическом виде, выходного сигнала , полученного численным решением ДУ и ошибки решения при шаге

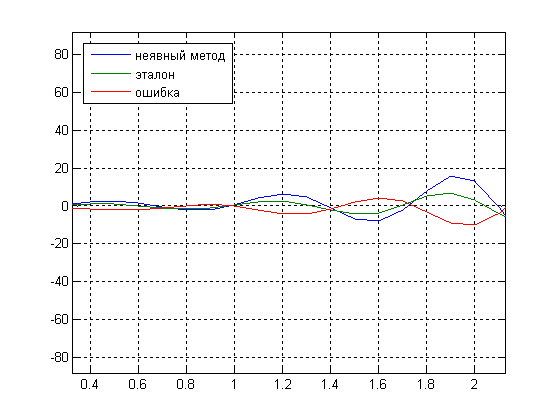
Рис.9. Графики выходного сигнала , полученного в аналитическом виде, выходного сигнала , полученного численным решением ДУ и ошибки решения при шаге

2.9 Анализа заданной системы с использованием спектрального метода (базис: Чебышева 2 рода)

Спектральная форма представления сигналов и временных динамических характеристик систем и объектов основана на их разложении в заданной системе ортогональных функций

Если некоторый сигнал  принадлежит пространству , т.е. для него справедливо положение

,

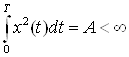То он может быть представлен в виде ряда Фурье:

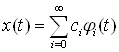 (14)

Если ввести векторы

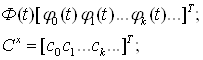
то ряд (14) можно представить следующим образом

 (15)

Совокупность коэффициентов Фурье  разложения сигнала  в ряд (14) называется спектральной характеристикой этого сигнала.

Коэффициенты Фурье  определяются по формуле

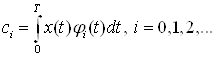 (16)

Существенным и определяющим отличием спектрального описания дискретных сигналов от спектрального описания непрерывных сигналов на конечных интервалах является возможность их точного представления в виде рядов Фурье с конечным числом членов. Значит, если дискретный сигнал, а данный сигнал имеет место на входе ЭВМ после его аналого-цифрового преобразования (АЦП), задан на конечном множестве точек, например , в виде некоторой числовой последовательности , то его разложение по заданной системе ортогональных функций

определяется соотношением

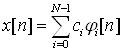 (17)

Система  - это система ортогональных, нормированных функций, удовлетворяющих условию

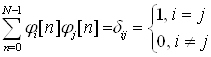
Коэффициенты Фурье  определяются по формуле

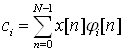 (18)

Далее вводим полиномы Чебышева 2-го рода (19):

 (19)

 

2.9.1 Алгоритм построения спектральной характеристики(СХ)

1. Исходные уравнение 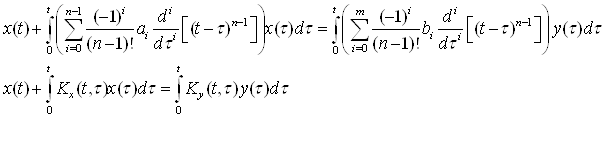(20):

(20)

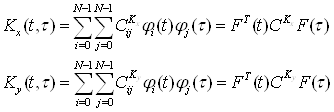Вычислим ядра  и  (21):

 (21)

 

3. Разложим  в ряды Фурье по заданному базису 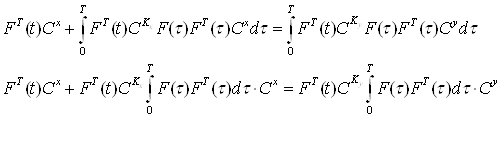(22):

(22)

4. Получим значение Сх из приведенных ниже преобразований 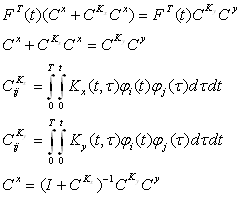(23):

(23)

5. Найдем матрицу А:

6. Получены значения ядер:

7. Воздействие:

 

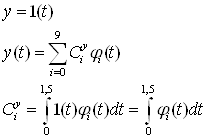
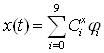
8. Значение вектора Cх:

9. Матрица А:

А=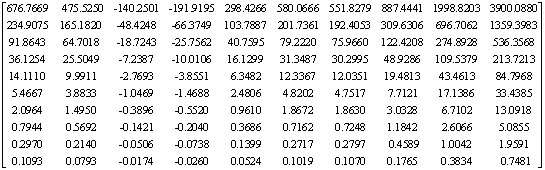

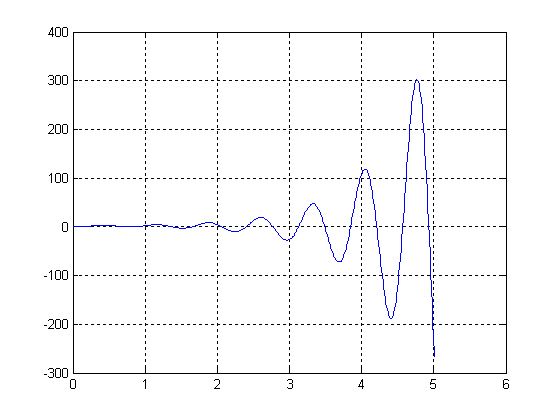
Рис.10 Переходная функция, построенная спектральным методом

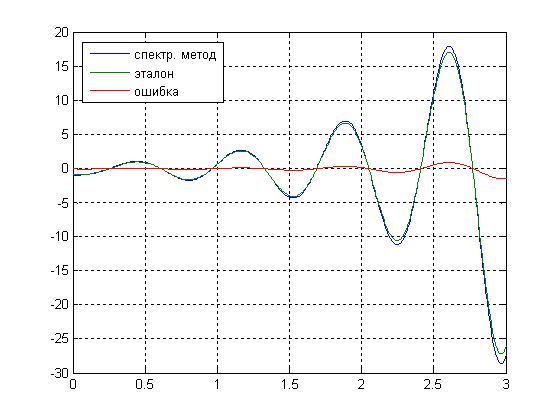
Рис.11 График выходного сигнала, полученного аналитически, сигнала, полученного спектральным методом и ошибки.