Навигация
3. СИНТЕЗ
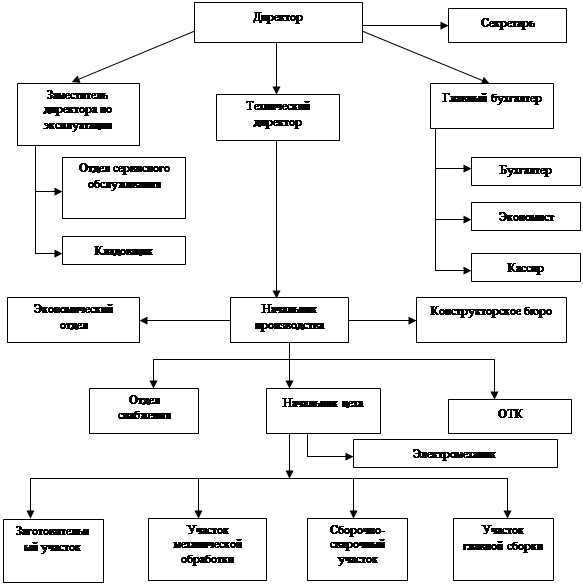
Исходные данные: структурная схема заданной системы изображена на рис. 12.
Введем в систему последовательное корректирующее устройство. В качестве регулятора выберем ПИД-регулятор.
Его передаточная функция имеет вид:
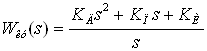(24)
Рис.12: Структурная схема заданной САУ с корректирующим устройством в прямой цепи.
3.1 Передаточная функция замкнутой цепи скорректированной САУ
Найдём передаточную функцию разомкнутой цепи, если известна передаточная функция объекта (25):
(25)
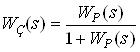
Передаточная функция замкнутой системы будет иметь вид 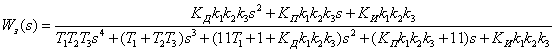(26):
(26)
Для решения задачи синтеза необходимо найти параметра регулятора 
, структура которого заданна (формула 31), при которых реальный выходной сигнал 
, являющийся реакцией на единичное ступенчатое воздействие, будет близок к заданному эталонному сигналу 
.
В качестве эталонного выходного сигнала выберем следующий сигнал:
, (27)
где параметр
находится по следующей зависимости:
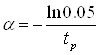. (28)
3.2 Функционал качества, подлежащий дальнейшей минимизации
Критерием близости выберем метрику пространства 
.
Тогда целевая функция, подлежащая минимизации по параметрам регулятора будет иметь следующий вид:
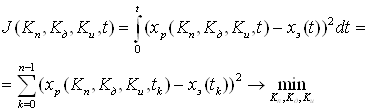(29)
3.2.1 Поиск минимума функции методом Фибоначчи
Если начальный интервал 
имеет длину 
, то произведя 
вычислений функции, можно уменьшить начальный интервал неопределённости в 
раз по следующей формуле:
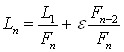(30)
по сравнению с его начальной длинной (пренебрегая 
).
Если определить последовательность чисел Фибоначчи следующим образом: 
для 
то можно найти положение первой точки, которая помещена на расстоянии 
от одного из концов начального интервала, причём не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии от конца интервала:
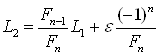. (31)
После того, как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение может определятся из практических соображений. Оно должно быть меньше 
, иначе будут иметь место лишние вычисления значений функции 
.
Таким образом, поиск методом Фибоначчи является итерационной процедурой.
В процессе поиска интервала 
с точкой 
, уже лежащей в этом интервале, следующая точка 
всегда выбирается такой, что 
.
Обозначим 
и 
, тогда можно рассмотреть четыре случая организации вычислительного процесса:
1. 
: новый интервал .
2. 
: новый интервал 
.
3. 
: новый интервал 
.
4. 
: новый интервал 
.
Оканчивать вычислительный процесс можно двумя способами. Либо выполнить намеченные ранее вычислений, либо, если в процессе вычислений интервал неопределённости станет меньше заданной величины.
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.. 3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном ...
... телеги, микропроцессорные системы и т.д. В данном дипломном проекте поставлена задача оптимизировать сборку телеги, а также выявить экономический эффект за счет инноваций технологии и экономии ресурсов. Рассмотрим основные составляющие телеги: - Полка ТМ.201.01.03 – 24 шт. – Лист Б-О-ПН-2,0 ГОСТ 19903-74/12Х18Н10Т ГОСТ 5582-75; - Заглушка ТМ.201.01.09 – ...
... Заключение В результате проведенного исследования, можно сделать следующие выводы. Для достижения поставленной цели в работе были поставлены и решены следующие задачи: 1. раскрыта сущность управленческого контроля и его особенности в туристском бизнесе; Каждая компания должна найти свой стиль работы, наилучшим образом учитывающий специфику условий, возможностей, целей и ресурсов. ...
0 комментариев