Навигация
3.2.2 Метод Хука-Дживса
В данном методе поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которым, в случае успеха, проводится поиск по образцу.
Процедура поиска следующая.
Выбрать начальную базисную точку 
и шаг длиной 
для каждой из переменных 
, 
.
Вычислить 
в базисной точке с целью получения сведений о локальном поведении функции . Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции.
При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом.
Завершить этот процесс, когда длина шага (длины шагов) будет уменьшаться до заданного малого значения.
3.3 Дифференциальное уравнение скорректированной системы
Для минимизации целевой функции (37) необходимо реализовать вычисление реального выходного сигнала 
в каждый отдельный момент времени. Помимо этого, необходимо реализовать итерационный процесс и реализовать алгоритм вычисления параметра 
Для вычисления перейдём от передаточной функции замкнутой цепи к дифференциальному уравнению, используя свойства преобразований Лапласа. Оно будет иметь следующий вид:
(32)
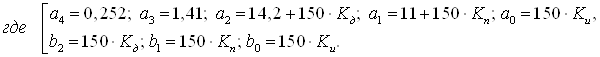
Запишем ДУ (32) в другом виде:
(33)
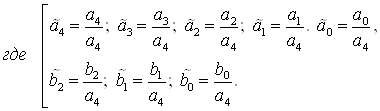
3.4 Нормальная форма Коши, полученного ДУ скорректированной системы
Для решения ДУ (33) с помощью численного метода решения дифференциальных уравнений, необходимо понизить его порядок, путём перехода от данного ДУ к нормальной форме Коши
Нормальная форма Коши для ДУ (33) будет иметь следующий вид:
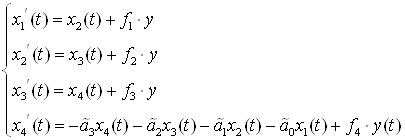
где коэффициенты 
рассчитываются по следующим формулам:
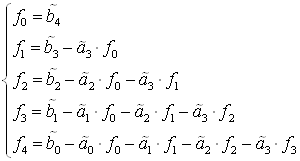
Тогда ДУ (33) можно записать в следующем виде
, (34)
где 
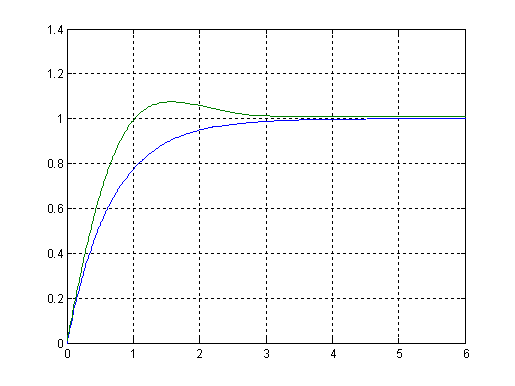
Рис. 13. Графики выходных сигналов скорректированной (зеленая линия) и нескорректированной (синяя линия) САУ.
Полученные параметры регулятора:
Кп=1.0547895
Кд=0.0550905
Ки=0.9452075
5. Выводы
Численные методы решения дифференциальных уравнений используются в тех случаях, когда не удается найти их решение в аналитическом виде. Прежде всего, это относится к линейным дифференциальным уравнениям с переменными коэффициентами и нелинейным дифференциальным уравнениям, соответственно описывающим динамику линейных нестационарных и нелинейных систем управления.
Сущность численных методов состоит в том, что решение ДУ строится только для дискретных значений аргумента.
Все численные решения ДУ делятся на две группы: одношаговые и многошаговые. В одношаговых методах используется информация о поведении решения в предыдущей точке. В многошаговых о поведении решения в нескольких предыдущих точках.
Численные решения ДУ можно разделить на две группы: явные и неявные. В явных методах, в отличие от неявных, используется явная зависимость значения функции в текущей точке от значений функции в предыдущих точках. Преимуществом таких методов является относительная простота вычисления значения функции на каждом шаге, однако, сходимость данных методов определяется шагом интегрирования 
.
В отношении численных методов оптимизации следует отметить следующее. Все численные методы минимизации делятся на прямые и градиентные методы. В прямых методах используется только значение функции в конкретных точках, а в градиентных - информация о первых и вторых производных функции. Также методы минимизации можно разделить на методы минимизации функции одной переменной и методы, позволяющие минимизировать функции многих переменных. При минимизации необходимо учитывать наличие ограничений на параметры исходной функции.
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.. 3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном ...
... телеги, микропроцессорные системы и т.д. В данном дипломном проекте поставлена задача оптимизировать сборку телеги, а также выявить экономический эффект за счет инноваций технологии и экономии ресурсов. Рассмотрим основные составляющие телеги: - Полка ТМ.201.01.03 – 24 шт. – Лист Б-О-ПН-2,0 ГОСТ 19903-74/12Х18Н10Т ГОСТ 5582-75; - Заглушка ТМ.201.01.09 – ...
... Заключение В результате проведенного исследования, можно сделать следующие выводы. Для достижения поставленной цели в работе были поставлены и решены следующие задачи: 1. раскрыта сущность управленческого контроля и его особенности в туристском бизнесе; Каждая компания должна найти свой стиль работы, наилучшим образом учитывающий специфику условий, возможностей, целей и ресурсов. ...
0 комментариев